Непрерывные случайные величины
Определение 1. Случайная величина называется непрерывной, если функция ее распределения всюду непрерывна, а производная функции распределения непрерывна во всех точках, за исключением, быть может, конечного числа точек на любом конечном интервале.
Примерами непрерывных случайных величин могут служить: диаметр детали, которую токарь обтачивает до заданного размера, рост человека, дальность полета снаряда и др.
Определение 2. Плотностью вероятности f(x) непрерывной случайной величины называется производная ее функции распределения F(x), т.е. f(x) = F'(x). (1)
Нормальное распределение
Случайная величина X распределена по нормальному закону, если ее плотность вероятности равна

Для нормального закона распределения:

Функция распределения нормально распределенной случайной величины

Функция F(x) связана с функцией Лапласа

Следует вспомнить из предыдущего раздела рекуррентную функцию вычисления функции Лапласа и используя ее составить функцию вычисления нормально распределенной случайной величины:
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if
x > 5
then FF := 1
else if x < -5
then
FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;

Для нормальной распределенной случайной величины X верны формулы

вероятность того, что X примет значения от



вероятность отклонения X от a
по модулю меньше, чем на


правило "трех сигм".
Примеры
1. Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Известно, что средняя квадратическая ошибка равна 3.6 мм.
Найти вероятность того, что длина наудачу взятой детали находится в границах а) от 55 мм до 68 мм; б) от 32 мм до 40 мм.
Математическое решение задачи
По условию

а)



б)

Для составления программы достаточно использовать функцию Муавра-Лапласа.
Программа
Program Normal1;
uses WinCrt;
var
a, a1, b, c, PP : real;
{----------------------------------------------------------------------------------------}
{ Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer; u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите математическое ожидание (проектную длину) a ');
readln(a);
write('Введите левую границу интервала '); readln(a1);
write('Введите правую границу интервала '); readln(b);
write('Введите среднюю квадратическую ошибку '); readln(c);
pp := 0.5*(FF((b - a)/c)-FF((a1 - a)/c));
write('Вероятность того, что деталь находится в ');
writeln('заданных границах равна ', pp:1:6)
end.
2. Автомат изготовляет шарики для подшипников. Шарик считаем принятым, если отклонение X диаметра шарика от заданного размера по абсолютной величине меньше 0.7 мм. Считается, что X распределена нормально со средним квадратическим отклонением

Решение
По условию задачи отклонение X шарика от заданного размера a есть случайная величина.
Следовательно, M(X) = 0. Допустимая ошибка отклонения



Тогда из 50 шариков в среднем будет принято 50

Программа
Program Normal2;
uses WinCrt;
var
e, c : real;
n : integer;
{----------------------------------------------------------------------------------------}
{ Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
begin
writeln('Введите отклонение X диаметра шарика');
write('от заданного размера по абсолютной величине '); readln(e);
write('Введите среднее квадратическое отклонение '); readln(c);
write('Введите число изготовленных шариков '); readln(n);
n := Round(FF(e/c)*n);
writeln('Число годных шариков равно ', n)
end.
3. Случайная величина X распределена нормально со средним квадратическим отклонением

Решение
В условии задачи дано, что




По формуле (5) получаем

Теперь остается найти аргумент функции Муавра-Лапласа. Для этого достаточно составить следующую небольшую процедуру:
{ Процедура нахождения аргумента функции Муавра-Лапласа }
Procedure
Argument(PP : real; var x : real);
begin
x := 0;
repeat
x := x + 0.0001
until FF(x) >= PP
end;
Процедуре организована с помощью цикла с последующим условием repeat
... until ... , в котором заведомо установлен шаг - 0.0001 для поиска аргумента. Однако этот шаг можно изменить или вводить в процедуру по усмотрению пользователя.
Тогда процедуру можно построить так:
{ Процедура нахождения аргумента функции Муавра-Лапласа }
Procedure
Argument(PP, eps : real; var x : real);
begin
x := 0;
repeat
x := x + eps
until FF(x) >= PP
end;
Новый способ задания случайной величины
Ранее дискретная случайная величина характеризовалась законом распределения. Однако задать случайную величину можно и иначе, например так называемой функцией распределения
Этот способ является более общим, чем предыдущий и приводит нас к рассмотрению непрерывных случайных величин.
Рассмотрим событие, состоящее в том, что случайная величина Y примет какое-нибудь значение, меньшее произвольного числа x, т.е. Y < x. Оно имеет определенную вероятность. Обозначим ее F(x) = P(Y < x).
При изменении x будут, вообще говоря, меняться вероятности


Определение. Функцией распределения случайной величины Y называется функция F(x), выражающая для каждого x вероятность того, что случайная величина Y примет какое-нибудь значение, меньшее x.
Будем говорить, что известно распределение случайной величины Y, если известна ее функция распределения F(x).
Пример 1. Пусть вероятность изготовления нестандартного изделия при некотором технологическом процессе равна 0.06. Контролер берет из партии изделие и сразу проверяет его качество. Если оно оказывается нестандартным, дальнейшие испытания прекращаются, а партия задерживается. Если же изделие оказывается стандартным, контролер берет следующее и т. д., но всего проверяет не более пяти изделий. Найти функцию распределения случайной величины Y - числа проверяемых изделий.
Решение
Нам известен закон распределения случайной величины:
| Число проверяемых изделий | 1 | 2 | 3 | 4 | 5 | ||||||
| Вероятность | 0.06 | 0.056 | 0.053 | 0.050 | 0.0781 |
Случайная величина Y не принимает значений, меньших 1. Следовательно, если x



Действительно, если, например, x = 1.2, то F(x) означает вероятность события

Покажем, что для всех x, удовлетворяющих двойному неравенству 2 < x




Аналогичными рассуждениями можно найти функцию распределения. Запишем ее в виде таблицы.
|
x |
x |
1<x |
2<x |
3<x |
4<x |
x>5 |
|
F(x) |
0 |
0.06 |
0.116 |
0.169 |
0.219 |
1 |
В программе обратите внимание на организацию форматированного вывода результата.
Program Function1; { Функция распределения случайной величины }
uses WinCrt;
Const
k = 20;
type
t = array[1..k] of integer;
tt = array[0..k] of real;
var
x : t; p : tt;
i, n : integer; pp : real;
begin
write('Введите общее число проверяемых изделий '); readln(n);
writeln('Вводите число изделий и соответствующие им вероятности');
for i := 1 to
n do
begin
write('Число изделий '); readln(x[i]);
write('Соответствующая вероятность '); readln(p[i])
end;
for i := 1 to n do write(x[i]:2+i*2); writeln;
for i := 1 to n do write(p[i]:1:4, ' ':3); writeln;
writeln('Значения аргумента функции распределения x');
write('(-бесконечность; ', x[1], ']; ':4);
for i := 1 to
n-1 do write('(', x[i], '; ',x[i + 1], ']', '; ':3);
write('(', x[n], '; +бесконечность)'); writeln;
write(' ',0:4, ' '); pp := 0;
for i := 1 to n - 1 do
begin
pp := pp + p[i];
write(pp:1:4, ' ':2)
end;
write(0:4, ' '); writeln
end.
Пример 2. Прибор состоит из двух блоков, вероятность безотказной работы каждого из которых в течение времени

Решение
Ряд распределения вероятностей
|
xi |
0 |
1 |
2 |
|
pi |
1/4 |
1/2 |
1/4 |
Если 0 < x


Если 1 < x


Если 2 < x <


Получаем

Свойства функции распределения: F(






Другими словами, функция распределения любой случайной величины является неубывающей функцией, а изменяется она от 0 до 1 при изменении x от


Программа
Program Function2; { Функция распределения случайной величины }
uses WinCrt;
Const
k = 20;
type
t = array[1..k] of integer;
tt = array[0..k] of real;
var
x : t;
p, pp : tt;
i, n, m : integer;
xx : real;
{----------------------------------------------------------------------------------------}
{ Функция распределения случайной величины }
Function Fx(xx : real) : real;
begin
if xx <= 0
then Fx := 0
else
if (xx > 0) and (xx <= 1)
then Fx := pp[1]
else
if (xx > 1) and (xx <= 2)
then Fx := pp[2]
else Fx := 1
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите общее число испытаний '); readln(n);
writeln('Вводите число испытаний и соответствующие им вероятности');
for i := 1 to
n do
begin
write('Число испытаний '); readln(x[i]);
write('Соответствующая вероятность '); readln(p[i])
end;
for i := 1 to n do write(x[i]:3+i*2); writeln;
for i := 1 to n do write(p[i]:1:4, ' ':3); writeln;
writeln(' Значения аргумента функции распределения x');
write('(-бесконечность; ', x[1], ']; ':4);
for i := 1 to
n-1 do write('(', x[i], '; ',x[i + 1], ']', '; ':4);
write('(', x[n], '; +бесконечность)'); writeln;
write(' ',0:4, ' ');
m := 0; pp[0] := 0;
for i := 1 to n - 1 do
begin
m := m + 1;
pp[m] := pp[m-1] + p[i];
write(pp[m]:1:4, ' ':2)
end;
write(1:4, ' '); writeln;
writeln('Функция распределения случайной величины');
write('Введите значение аргумента '); readln(xx);
writeln('Значение функции F(x) равно ' , Fx(xx):1:4)
end.
Вероятность попадания случайной величины X в промежуток [a; b) определяется формулой

Операции отношения или сравнения
| Знак | Наименование | Пример | Пояснение | ||||
| < | Меньше | a < 6 | a меньше 6 | ||||
| <= | Меньше или равно | b <= 23 | b меньше или равно 23 | ||||
| > | Больше | x > 5 | x больше 5 | ||||
| >= | Больше или равно | y >= 8 | y больше или равно 8 | ||||
| = | Равно | c = 10 | c равно 10 | ||||
| <> | Не равно | d <> 3 | d не равно 3 |
Оператор цикла fordowntodo
Существует другая форма оператора цикла for:
for <пар .цик.> := <нач. зн.> downto <кон. зн.> do
<оператор>.
Замена зарезервированного слова to на downto
означает, что шаг параметра цикла равен (-1).
Изменение значения параметра идет от большего значения к меньшему, т. е. <нач. знач.>

Программу вычисления факториала числа можно составить, используя этот оператор цикла.
Программа
Program Problem1a;
uses WinCrt;
var
n, i, f : longint;
begin
write('Введите натуральное число '); readln(n);
f := 1;
if n <> 0 then for i := n downto 1 do f := f*i;
writeln('Факториал числа ', n, ' равен ', f)
end.
Графическое изображение циклов for будет таким (см. рис. 22):
Рис. 22

Задание 1
1. Выполните программу примера 1 на компьютерах.
2. Измените и дополните ее так, чтобы она вычисляла следующую сумму:
1! + 2! + 3! + ... + n!.
Разберем другие, на мой взгляд, более интересные примеры с использованием циклов for
... to ... do ..., а также вложенных друг в друга циклов (циклов в циклах), совмещение циклов с параметром с другими циклами.
Пример 2. Квадрат любого натурального числа n равен сумме n первых нечетных чисел:
12 = 1
22 = 1 + 3
32 = 1 + 3 + 5
42 = 1 + 3 + 5 + 7
52 = 1 + 3 + 5 + 7 + 9
. . . . . . . . . . . . . . . . . . .
Основываясь на этом свойстве, составить программу, позволяющую напечатать квадраты натуральных чисел от 1 до n.
Ясно, что цикл в программе надо организовать от 1 до n, в котором выполнять всего три оператора: находить сумму нечетных чисел (а их как раз столько, сколько раз будет выполняться цикл); выдавать полученную сумму на экран; "получать" следующее нечетное число.
Программа
Program Problem2;
uses WinCrt;
var
i, n, s, k: integer;
begin
writeln(' Введите натуральное число, до которого надо');
write('выводить квадраты чисел '); readln(n);
writeln('Квадраты чисел следующие:');
s := 0; k := 1;
for i := 1 to n do
begin
s := s + k;
writeln('Квадрат числа ', i, ' равен ', s);
k := k + 2
end
end.
Задание 2
1. Измените программу так, чтобы она выдавала на экран не таблицу квадратов чисел от 1 до n, а квадрат только одного числа n, введенного пользователем.
2. Измените и дополните программу так, чтобы она выдавала значение квадрата числа и те нечетные числа, сумме которых он равен.
3. Продолжая тему возведения натуральных чисел в степень, без операций умножения, рассмотрим еще два интересных примера. В первом из них нам придется совмещать, "вкладывать" друг в друга два цикла for, а во втором, циклы for и repeat.
Пример 3. Куб любого натурального числа n равен сумме n нечетных чисел, следующих по порядку за числами, сумма которых составляла куб предыдущего числа n - 1:
13 = 1
23 = 3 + 5
33 = 7 + 9 + 11
43 = 13 + 15 + 17 + 19
. . . . . . . . . . . . . . . . . . . . . .
Основываясь на этом свойстве, создайте программу, позволяющую напечатать таблицу кубов натуральных чисел.
Вот здесь уже нужны два цикла. Один - внешний, по количеству нечетных чисел, которое равно возводимому в куб числу, например, для 43 этот цикл должен выполняться 4 раза. В этом же цикле надо будет после подсчета суммы выводить ее значение на экран вместе с числом, которое возводится в куб.
Второй - внутренний, который будет суммировать нечетные числа и "вырабатывать" нужные нечетные числа для суммирования.
Программа
Program
Problem3; { Кубы натуральных чисел от 1 до n }
uses WinCrt;
var
i, j, n, s, k : longint;
begin
writeln('Введите натуральное число, до которого надо');
write('выводить кубы чисел '); readln(n);
writeln('Кубы чисел следующие:');
k := 1;
for i := 1 to n do
begin
s := 0;
for j := 1 to i do
begin
s := s + k; k := k + 2
end;
writeln('Куб числа ', i, ' равен ', s)
end
end.
Разберем работу этой программы
Переменные i и j нужны в качестве переменных первого - внешнего и второго - внутреннего циклов. Переменная k для нечетных чисел, а s для суммы чисел. Тип этих переменных установлен целый, но longint, так как могут быть достаточно большие целые числа, большие 32767.
Программа начинается с запроса для пользователя с помощью операторов writeln и write о вводе натурального числа, до которого надо выдавать таблицу кубов чисел. Затем с помощью оператора readln это значение вводится в память компьютера и присваивается переменной n.
Выводится надпись "Кубы чисел следующие". Она дана перед началом циклов по понятным причинам. В циклах ее дать нельзя, - она будет повторяться несколько раз. По окончании циклов тоже, тогда она будет написана внизу, после вывода самих чисел. Переменной k присваивается первое нечетное значение 1.
Начинается внешний цикл по количеству чисел, от 1 до n. В цикле несколько операторов, поэтому "открываются" операторные скобки: - begin ...
Перед началом внутреннего цикла обнуляется переменная s - сумма. Причем такое обнуление будет происходить каждый раз, когда повторяется внешний цикл, перед началом выполнения внутреннего цикла.
Внутренний цикл выполняется от 1 до i. Почему? В цикле вычисляется сумма и увеличивается нечетное k на 2, т. е. "вырабатывается" следующее нечетное число.
Заметьте!
Переменной k не присваивается перед началом каждого внутреннего цикла 1. Почему?
Следующим оператором writeln внутри внешнего цикла выдается информация на экран. Почему он размещен во внешнем цикле?
Пример 4. Из математики известно, что всякая натуральная степень числа n есть сумма n последовательных нечетных натуральных чисел. Составьте программу, которая для любой степени натурального числа n находила бы последовательность нечетных чисел, сумме которых равна эта степень.
Например, для 53 она выдавала бы последовательность чисел: 21, 23, 25, 27, 29.
План составления программы
1. Определим цель составления программы: надо показать, что действительно любую натуральную степень натурального числа можно представить в виде суммы последовательных нечетных чисел.
А если это так, тогда нам совершенно необходимо знать значение степени числа n с показателем k.
Это можно сделать с помощью простого цикла:
s := 1;
for i := 1 to k do s := s*n;
Значение степени будут накапливаться в переменной s, для этого ей устанавливается первоначальное значение 1.
В цикле, значение переменной s последовательно, k раз умножается на основание степени n. После выполнения цикла переменная s получит значение степени числа n с показателем k.
2. Вся острота вопроса состоит в том, что неизвестно первое нечетное число, от которого надо начинать суммирование последовательных нечетных чисел.
Для этого надо пробовать складывать нечетные числа вначале от 1 и далее (известно их количество - n);
1 + 3 + 5 + 7 + 9 ...,
а затем проверять полученный результат, сравнивая со значением степени s. Если равенство выполняется, тогда закончить цикл и вывести на экран полученные нечетные числа, если равенство не выполняется, тогда надо начинать суммирование со следующего нечетного числа - 3: 3 + 5 + 7 + 9 ... и т.д.
Этот процесс легче организовать с помощью цикла repeat. Переменной j, которая будет задавать начальные нечетные числа надо установить перед началом цикла первоначальное значение 1.
Общий вид такого цикла:
j := 1;
repeat
. . . . . .
j := j + 2
until ...= s;
3. Осталось продумать, как подсчитывать суммы последовательных нечетных чисел. Мы уже сталкивались с этим вопросом и знаем, что для этого надо создать цикл от 1 до n, в котором в одну из переменных, скажем m, накапливать эту сумму, а вторая переменная должна "вырабатывать" следующее нечетное число.
Этот цикл можно записать так:
p := j; m := 0;
for i := 1 to n do
begin
m := m + p; p := p + 2
end;
Обратите внимание! Переменная p, каждый цикл repeat, (внешний по отношению к данному), будет получать новое начальное значение нечетного числа, а переменная m - для суммы должна обнуляться перед каждым новым суммированием для другой последовательности нечетных чисел.
4. Наконец, когда последовательность нечетных чисел найдена, ее надо вывести на экран. Для этого надо устроить еще один цикл от 1 до n, в котором выдавать значения этих нечетных чисел. За первое нечетное число из последовательности надо взять значение j, но так как оно уже увеличилось на 2, то из j следует вычесть 2. Этот цикл будет:
j := j - 2;
for i := 1 to n do
begin
write(j, ' ');
j := j + 2
end
Программа
Program Problem4;
uses WinCrt;
var
n, i, k, j, m, s, p : longint;
begin
write('Введите натуральное число - основание степени '); readln(n);
write('Введите натуральное число - показатель степени '); readln(k);
s := 1; j := 1;
for i := 1 to k do s := s*n;
repeat
p := j; m := 0;
for i := 1 to n do
begin
m := m + p;
p := p + 2
end;
j := j + 2
until m=s;
write('Степень с основанием ', n);
writeln(' и показателем ', k, ' т. е. ', s);
writeln('равна сумме следующих нечетных чисел');
j := j - 2;
for i:=1 to n do
begin
write(j, ' ');
j := j + 2
end
end.
Чтобы лучше понять ее работу, возьмите степень 25 и проверьте как будут последовательно выполняться операторы программы.
Задание 3
1. Выполните эту программу на компьютерах.
2. Составьте программу, которая выясняет, может ли произведение а) трех; б) четырех последовательных натуральных чисел равняться некоторой степени некоторого натурального числа (квадрату, кубу, и т. д.)?
Оператор if then else
Многие представляют ЭВМ как чисто вычислительную машину, что является заблуждением. ЭВМ способна, подобно человеку, принимать решения.
Вот некоторые простые решения, которые принимает человек в зависимости от условия.
Если
пойдет дождь, тогда надо взять зонтик,
иначе, зонтик не брать.
Если в комнате темно, тогда надо включить свет.
Человек, принимая какое-то решение, может сомневаться, взвешивать, прикидывать, машина принимает решения категорически: либо - да, либо - нет и никаких сомнений.
Для реализации принимаемых решений на языке Паскаль могут быть использованы операторы if
(если), then (тогда) и else (иначе).
После оператора if записывается условие, а после операторов then и else - команды, которые необходимо выполнить.
Для более ясного понимания использования этих операторов, рассмотрим следующий пример.
Пример 2. Составить программу, после выполнения которой меньшее из двух неравных чисел будет увеличено вдвое, а большее оставлено без изменения.
Программа
Program
Problem2; { Увеличения меньшего из двух целых чисел вдвое }
uses WinCrt;
var
a, b, c : integer;
begin
write('Введите первое целое число '); readln(a);
write('Введите второе целое число '); readln(b);
if a < b then c := 2*a
else c := 2*b;
writeln('Меньшее число ', c div 2);
writeln('Оно же увеличенное вдвое ', c)
end.
После пуска программы вводятся два целых числа и их значения присваиваются переменным a и b. Далее, в операторе if проверяется условие (a<b), если оно выполняется, т.е. a меньше b, тогда выполняются команды в операторе then, переменной c присваивается значение удвоенного числа a, иначе выполняются команды в операторе else, переменной c присваивается значение удвоенного меньшего числа - b.
После этого выводится на экран меньшее число и это же число, но увеличенное вдвое.
Заметьте,
в процедуре writeln, кроме вывода информации, выполняется еще и деление переменной c на 2.
В процедуре write (writeln) можно записывать выполнение арифметических операций.
Ещё одно существенное замечание. Вы уже заметили, что перед оператором else
точка с запятой не ставится.
Программа имеет один недостаток. В ней не учитывается то, когда введенные числа будут равны. В этом случае на экран надо выдать сообщение: "Числа равны".
Программа
Program
Problem2a; {Программа удвоения меньшего из двух чисел}
uses WinCrt;
var
a, b, c : integer;
begin
write('Введите первое число '); readln(a);
write('Введите второе число '); readln(b);
if a = b then writeln('Числа равны')
else
begin
if a < b then c := 2*a
else c := 2*b;
writeln('Меньшее число ', c div 2);
writeln('Удвоенное меньшее число ', c)
end
end.
В этой программе два условных оператора, первым проверяется условие равенства чисел и, в случае его выполнения, будет выдано сообщение о равенстве чисел, которое находится в операторе then.
В операторе else
записано несколько команд, поэтому в нём установлены операторные скобки:
begin
........
end;
Такие же операторные скобки в необходимых случаях могут быть использованы и в операторе then.
ВЫВОДЫ
В операторах then и else могут быть использованы операторные скобки:
begin ... end;,
где записывается еще одна группа операторов.
Перед оператором else точка с запятой не ставится.
Задание 2
1. Введите первую программу примера 2 и выполните ее. Измените программу так, как это было сделано во втором случае, т. е. с учетом равенства вводимых чисел.
2. Составьте программу определения большего из двух чисел.
3. Составить программу определения модуля числа.
Операторы read и readln Процедуры ввода информации

Операторы read (считывать) и readln, который происходит от двух английских слов read (считывать) и line (строка) используются в программах для ввода информации в память компьютера и "считывания" значений в переменную.
Рассмотрим работу этих операторов и процедур ввода информации.
В нашей программе есть процедура readln(a). При выполнении программы, встретив оператор readln, компьютер приостановит работу в ожидании ввода информации. После того, как мы введем с клавиатуры значение переменной a - 16, компьютер присвоит это значение переменной a, т.е. отправит его в ячейку памяти с именем a и продолжит выполнение программы. Этот процесс мы называем "считыванием" значения в переменную.
Итак, процедуры read и readln "считывают" значения переменных и присваивают их тем переменным, которые записаны в них.
Таких переменных может быть несколько, тогда они записываются в этих операторах через запятую, например:
read(a, b, c, n, g, j, i), readln(e,f, k, p, d) и т.п.
Чем же отличается работа процедур read и readln?
Процедура read потребует после себя ввод или вывод информации в одну строку, а процедура readln дает возможность после себя вводить и выводить информацию с начала новой строки.
Например:
В программе: write('Введите значения a и b '); read(a, b);
write('Ввод информации в одну строку');
При выполнении этой части программы, на экран будет выведено все то, что записано в первом операторе write, затем в той же строке будет находиться курсор, и компьютер будет ждать ввода значений a и b. Введем их значения - 2 и 3, разделяя их пробелом или, иначе говоря, через пробел. После этого, в той же строке будет выдана информация записанная в следующем операторе write.
На экране:
Введите значения a и b 2 3 Ввод информации в одну строку
В программе:
writeln('Введите значения a, b и c); readln(a, b, c);
writeln('Ввод и вывод информации с начала строки');
На экране:
Введите значения a, b и c
2 3 4
Ввод и вывод информации с начала строки
Операторы write и writeln Процедуры вывода информации


Кроме операторов write и writeln мы говорим о процедурах вывода информации.
Что же такое процедура?
Понятие процедуры - одно из основных понятий Паскаля. Ему подобна подпрограмма на языке Бейсик.
Процедура - это некоторая последовательность операторов языка Паскаль, имеющая имя и к которой можно обратиться из любого места основной программы, указав ее имя.
Выше мы говорили об операторах вывода информации, хотя в Паскале, в отличие от Бейсика нет операторов вывода информации, а через служебные слова write и writeln происходит обращение к стандартной или встроенной
процедуре вывода информации. Стандартная процедура не нуждается в предварительном описании, она доступна любой программе, в которой содержится обращение к ней. Вот почему обращение к write или writeln напоминает оператор PRINT - вывода информации на языке Бейсик.
Разница между оператором вывода и обращением к процедуре вывода состоит в том, что имя процедуры вывода, как и любой другой процедуры Паскаля не является зарезервированным словом, а, следовательно, пользователь может написать свою собственную процедуру с именем write или writeln. Но это очень редко используется на практике.
Таким образом, операторы write и writeln являются операторами обращения к встроенным процедурам вывода информации.
Обе эти процедуры выводят информацию на экран, если эта информация содержится в виде значений переменных, тогда достаточно в скобках в операторах write или writeln записать имена этих переменных, например: write(a), writeln(f). Если таких переменных несколько, то их записывают через запятую, например: write(a, b, c, d), writeln(e,f, g, h).
Если информацией являются слова, предложения, части слов или символы, тогда она заключается между знаками " ' " - апостроф, например:
write('Введите длину пути'),
writeln('Значение скорости равно'
Возможен одновременный вывод и символьной информации и значений переменных, тогда в операторе write или writeln они разделяются запятыми, например:
write('Значение температуры равно ', t),
writeln('Скорость равна ', v, ' при времени движения ', t).
Заметьте, в конце слов, перед апострофом оставлен пробел.
Для чего это сделано? Конечно, чтобы следующая числовая информация была разделена со словами пробелом.
В чем состоит отличие
в работе процедур write и writeln?
Процедура write требует от следующих процедур ввода или вывода, информацию вводить или выводить ее на ту же строку (в одну строку).
Если в программе указан оператор write и за ним следуют еще операторы write или writeln, то выводимая ими информация будет присоединяться к строке информации первого оператора write.
Например: write('Сегодня и завтра будут ');
write('выходные дни ');
На экран выводится:
Сегодня и завтра будут выходные дни
Пробел между словом "будут" и "выходные" обеспечивается за счет пробела в конце первой строки. Если его не будет, то вывод произойдет слитно:
write('Сегодня и завтра будут');
write('выходные дни');
Сегодня и завтра будутвыходные дни
Еще некоторые примеры: t:=20;
write('Время движения равно ');
write(t);
write(' секунд');
Время движения равно 20 секунд
a := 18; b := 12;
write('Сумма чисел равна ');
write(a+b);
write(', а произведение ');
write(a*b);
Сумма чисел равна 30, а произведение 216
Процедура writeln обеспечивает для следующих процедур ввода или вывода информации вводить или выводить ее с начала каждой новой строки.
В программе:
writeln('Сегодня вечером, вечером, вечером,');
writeln('Когда пилотам, скажем прямо, делать нечего');
На экран выводится:
Сегодня вечером, вечером, вечером,
Когда пилотам, скажем прямо, делать нечего
В программе:
a := 25;
b := 17;
writeln('Сумма и разность чисел равны:');
writeln(a + b);
writeln(a - b);
На экране:
Сумма и разность чисел равны:
42
8
Определение законов распределения дискретных величин эмпирическим (опытным) путем
Как мы уже знаем, для случайного события статистическим аналогом вероятности служит относительная частота, которую можно получить, повторяя опыт или наблюдение n раз и регистрируя относительную частоту m/n появления события.
Тогда закон распределения вероятностей можно записать в виде следующей таблицы:
| X |  |  | ... |  | |||||
| Относительная частота |  |  | ... |  |
При достаточно большом числе n повторений испытания мы вправе считать, что относительны частоты mi/n будут близки к соответствующим вероятностям pi= P(X = xi) (i = 1, 2, ..., k).
Попытаемся программными средствами Турбо Паскаля построить закон распределения числа очков, выпадающей на верхней грани игральной кости.
Составить процедуру, подсчитывающую относительные частоты выпадения очков нетрудно. Она может быть построена так:
Procedure Game(n, num : longint; var p : real);
var
m, x, i : longint;
begin
randomize;
m := 0;
for
i := 1 to n do
begin
x := random(6) + 1;
if
x = num then m := m + 1
end;
p := m/n
end;
Здесь, переменная n - число повторений испытания, которые задет пользователь, num - число очков на верхней грани игральной кости, вероятность выпадения которых надо определить, - это 1, 2, 3, 4, 5 или 6.
С помощью функции случайных чисел random(6) + 1 вырабатывается случайное целое число из промежутка [1, 6], т.е., по сути дела, моделируется выпадение числа очков при "бросание" игральной кости.
С помощью условного оператора if x = num then m := m + 1 подсчитывается число появления указанного числа очков при повторении испытания (бросания).
После завершения цикла, определяется относительная частота появления заданного числа очков и выводится в переменной p.
Программа
Program Problem1;
uses WinCrt;
var
n, num : longint;
p : real;
{----------------------------------------------------------------------------------------}
Procedure Game(n, num : longint; var
p : real);
var
m, x, i : longint;
begin
randomize;
m := 0;
for i := 1 to n do
begin
x := random(6) + 1;
if x = num then m := m + 1
end;
p := m/n
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите число повторений испытания '); readln(n);
writeln('Введите число очков, вероятность');
write('выпадения которых надо найти '); readln(num);
Game(n, num, p);
writeln('Относительная частота появления события ', p:1:9);
writeln('Сравните с теоретически найденной вероятностью ', 1/6:1:9)
end.
Можно видеть, что при увеличении числа повторений испытания относительная частота приближается к теоретически предсказанной вероятностью.
Однако возникают много вопросов. Самый первый из них - сколько повторений испытания надо сделать, чтобы с достаточной уверенностью можно было утверждать, что относительная частота равна вероятности? Какова степень этой "уверенности" или, выражаясь более точно, достоверности (достаточной уверенности)?
Чтобы ответить на эти и другие вопросы, надо обратиться к "числовым характеристикам распределения".
Сумма цифр числа равна
К заданию 1
Program
Task1;
uses WinCrt;
var
a, e, d, s, t, s1, p : integer;
begin
write('Введите четырехзначное число '); readln(a);
e := a mod 10; a := a div 10;
d := a mod 10; a := a div 10;
s := a mod 10; t := a div 10;
s1 := e + d + s + t; {Сумма цифр}
p := e*d*s*t; {Произведение цифр}
writeln(' Сумма цифр числа равна ', s1);
writeln('Произведение цифр равно ', p)
end.
К заданию 2
Задача 2
Program Task2_2;{Определение большего из двух чисел}
uses WinCrt;
var
a, b, c : integer;
begin
write('Введите первое число '); readln(a);
write('Введите второе число '); readln(b);
if a = b then writeln('Числа равны')
else if a > b then writeln('Большее число ', a)
else
writeln('Большее число ', b)
end.
Задача 3
Program Task2_3;{Определение модуля числа}
uses WinCrt;
var
a : integer;
begin
write('Введите целое число '); readln(a);
if a >= 0 then writeln('Модуль числа ', a, ' равен ', a)
else writeln('Модуль числа ', a, ' равен ', -a)
end.
К заданию 3
Program
Task3; { Решение уравнения ax = b }
uses WinCrt;
var
a, b : real;
begin
write('Введите первый коэффициент '); readln(a);
write('Введите свободный член '); readln(b);
if
a <> 0 then writeln('Уравнение имеет одно решение ', b/a:6:3)
else if (a = 0) and (b <> 0)
then
writeln('Уравнение не имеет решений')
else writeln('Уравнение имеет б/м решений')
end.
К заданию 4
Program
Task4; { Входят ли четные цифры в запись трехзначного числа? }
uses WinCrt;
var
a, s, d, e : integer;
begin
write('Введите трехзначное число '); readln(a);
e := a mod 10; a := a div 10; d := a mod 10; s := a div 10;
if (s mod 2 = 0) or (d mod 2 = 0) or (e mod 2 = 0)
then writeln('Четные цифры входят в запись этого числа')
else writeln('Четные цифры не входят в запись числа')
end.
К заданию 2
Задача 2
1-й способ
Program Task2_2;
uses WinCrt;
var
n, p, n1 : longint;
begin
write('Введите натуральное число n '); readln(n);
n1 := 0;
while n > 0 do
begin
p := n mod 10;
n1 := n1*10 + p;
n := n div 10
end;
writeln('Число, после перестановки цифр ', n1 + n)
end.
2-й способ
Program Task2_2a;
uses WinCrt;
var
n, p, n1 : longint;
begin
write('Введите натуральное число '); readln(n);
n1 := 0;
while n > 0 do
begin
n1 := n1*10 + n mod 10;
n := n div 10
end;
writeln('Число, после перестановки цифр равно ', n1)
end.
К
заданию 3
Задача 2
Program Task3_2;
uses WinCrt;
var
n, a, p, b, s : integer;
begin
write(' Введите натуральное число меньшее 28 '); readln(a);
b := 100;
writeln('Трехзначные числа, сумма цифр которых');
write('равна числу ', a, ' следующие: ');
while b < 1000 do
begin
s := 0; n := b;
while n <> 0 do
begin
p := n mod 10;
s := s + p;
n := n div 10
end;
if s = a then write(b, ', ');
b := b + 1
end; writeln
end.
Задача 3
Program Task3_3;
uses WinCrt;
var
n, d, e : integer;
begin
n := 10;
write('Искомое двузначное число ');
while n <= 99 do
begin
d := n div 10; e := n mod 10;
if n + d*d*d + e*e*e = e*10 + d then
writeln(n);
n := n + 1
end
end.
К
заданию 4
Program Task4;
uses WinCrt;
var
n, a, p, b, s : integer;
begin
write('Введите натуральное число '); readln(a);
b := 1;
writeln('Натуральные числа, сумма цифр ');
write('которых равна числу ', a, ' следующие: ');
while b < 32767 do
begin
s := 0; n := b;
while n <> 0 do
begin
p := n mod 10; s := s + p; n := n div
10
end;
if s = a then write(b, ', ');
b := b + 1
end; writeln
end.
К
заданию 1
Program Task1;
uses WinCrt;
var
n, a, k : integer;
begin
n := 131;
repeat
n := n + 131;
a := n; k := 0;
repeat
k := k + 1;
a := a div 10
until a = 0;
until k mod 2 = 0;
writeln('Наименьшее натуральное число, кратное 131');
writeln(' с четным количеством цифр равно ', n)
end.
К
заданию 2
Program Task2_2;
uses WinCrt;
var
a, n, p, s : integer;
begin
a := 100;
writeln('Трехзначные числа, при делении которых на 11');
write('частное равно сумме квадратов их цифр следующие ');
repeat
n := a; s := 0;
repeat
p := n mod 10;
s := s + p*p;
n := n div 10
until n = 0;
if (a mod 11 = 0) and (s = a div
11) then write(a, '; ');
a := a + 1
until a = 1000;
end.
К заданию 4
Program
Task4; { НОК двух чисел. 1 - способ }
uses WinCrt;
var
a, b, m, n, p : integer;
begin
write('Введите первое число '); readln(a);
write('Введите второе число '); readln(b);
p := 0;
repeat
if a>b then
begin
m := a; n := b
end
else
begin
m := b; n := a
end;
p := p + m
until p mod n =0;
writeln('НОК чисел ', a, ' и ', b, ' равен ', p)
end.
К заданию 5
Program
Task5; { Является ли число простым? 2- способ }
uses WinCrt;
label 1, 2;
var
n, i : integer;
begin
write('Введите целое число '); readln(n);
i := 3;
if n = 2 then writeln('Число ', n, ' - простое')
else if n = 3
then writeln('Число ', n, ' - простое')
else
if n mod 2 = 0 then
writeln('Число ',n,' составное')
else
repeat
if
n mod i = 0 then goto 1;
i := i + 2
until
i > n div 2;
writeln('Число ', n, ' простое'); goto 2;
1: writeln('Число ', n, ' составное');
2: end.
К заданию 1
Program
Task1;
uses WinCrt;
var
n, s, s1 : integer;
{----------------------------------------------------------------------------------------}
Procedure extent(a, n : integer; var s : integer);
var
i : integer;
begin
i := 1; s := 1;
repeat
s := s*a; i := i + 1
until i = n
end;
{----------------------------------------------------------------------------------------}
begin
n := 1;
repeat
n := n + 1;
extent(2, n, s);
extent(3, n, s1);
until ((s - 2) mod (n - 1) <> 0) and
((s1 - 3) mod (n - 1) = 0);
writeln(' Искомое число равно ', n - 1)
end.
К
заданию 2
Program Task2;
uses WinCrt;
var
n, s, s1 : integer;
{----------------------------------------------------------------------------------------}
Procedure extent(a, n : integer; var s : integer);
var
i : integer;
begin
i := 1;
s := 1;
repeat
s := s*a;
i := i+1
until i=n
end;
{----------------------------------------------------------------------------------------}
begin
n := 1;
repeat
n := n+1;
extent(2, n, s);
extent(3, n, s1);
until ((s-2) mod (n-1)<>0) and
((s1-3) mod (n-1)=0);
writeln('Искомое число равно ', n-1)
end.
К заданию 3
Program Task3; { Сумма правильных делителей }
uses WinCrt;
var
i, a, b, s : integer;
{----------------------------------------------------------------------------------------}
Procedure math_divisor(n : integer; var s : integer);
var
d : integer;
begin
s := 0;
for d := 1 to n div 2 do
if n mod d = 0 then s := s + d
end;
{----------------------------------------------------------------------------------------}
К заданию 1
К примеру 1
Program Task1;
uses WinCrt;
var
p : longint;
{----------------------------------------------------------------------------------------}
Procedure placement(n, k : integer; var r : longint);
var
i : integer;
begin
r := 1;
for i := 1 to k do r := r*(n - k + i)
end;
{----------------------------------------------------------------------------------------}
begin
placement(40, 3, p);
writeln('Число различных способов равно ', p)
end.
К
примеру 2
Program Task1_2;
uses WinCrt;
var
s, r1, r2, r3 : longint;
{----------------------------------------------------------------------------------------}
Procedure placement(n, k : integer; var r : longint);
var
i : integer;
begin
r := 1;
for i := 1 to k do r := r*(n - k + i)
end;
{----------------------------------------------------------------------------------------}
begin
placement(5, 1, r1);
placement(5, 2, r2);
placement(5, 3, r3);
s := r1 + r2 + r3;
writeln(' Не более чем трехзнач. чисел можно составить');
writeln('из цифр 1, 2, 3, 4, 5; ', s, ' способами')
end.
К заданию 2
К примеру 1
Program Task2_1;
uses WinCrt;
var
p1, p2, p : longint;
m, n : integer;
{----------------------------------------------------------------------------------------}
Procedure placement(n, k : integer; var r : longint);
var
i : integer;
begin
r := 1;
for i := 1 to k do r := r*(n - k + i)
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите число всех элементов '); readln(m);
write('Введите число выбираемых элементов '); readln(n);
placement(m, n, p1);
Переменные и их имена

Если "заглянуть" в компьютер, то переменную можно определить так.
Переменная - это имя физического участка в памяти, в котором в каждый момент времени может быть только одно значение.
Само название "переменная" подразумевает, что содержимое этого участка может изменяться.
В качестве имен переменных в Паскале могут быть латинские буквы с индексами. Причем может быть не одна буква, а несколько.
В качестве числового индекса может быть любое целое число. Всего в обозначении переменных может быть произвольное число символов, но значащими считаются первые 63 символа. В некоторых версиях Паскаля допускаются имена переменных, содержащие до 8 символов.
Примеры обозначений переменных: a, b, e, vert, trenin, d, f1, g23, p564, red18 и т.п.
Имена переменных называются идентификаторами.
Замечания
Не имеет значение в обозначении переменных маленькими или большими (строчными или прописными) буквами они написаны!
Имя переменной должно удовлетворять следующим требованиям:
1) всегда начинаться с буквы, после которой при необходимости может следовать некоторое целое число (индекс);
2) в идентификаторе (имени) не должно быть пробелов, запятых или других непредусмотренных знаков, например недопустимы следующие имена переменных: jan.2 (есть точка); 3x (начинается с цифры); a 2 (имеется пробел); чн (русские буквы);
3) нельзя использовать в качестве имен переменных слова, которые являются служебными или операторами, например: program, begin, write, end и другие.
Перестановки
Пример 6. Каким числом способов 10 человек могут находиться в очереди?
Рассуждая над этой задачей, нам становится понятным, что необходимо 10 элементов (10 человек) разместить на 10 местах в очереди, т.е. необходимо выполнить размещения
из 10 элементов по 10 -








Размещения из n
элементов по n называются перестановками из n элементов. Таким образом, две различные перестановки из n элементов могут отличаться друг от друга не числом элементов, а только порядком расположения элементов.
Определение. Пусть имеется конечное множество M = {a1, a2, ..., an}. Всякое упорядоченное множество, состоящее из n элементов множества M, называется перестановкой этого множества.
Согласно определению, число всевозможных различных перестановок из n элементов равно:

Не забывайте, что принято 0! = 1.
Для решения нашей задачи, надо составить программу с процедурой вычисления факториала числа.
Program Problem6;
uses WinCrt;
var
n, f : longint;
{----------------------------------------------------------------------------------------}
Procedure Factorial(n : integer; var
f : longint);
var
i : integer;
begin
f := 1;
if n = 0 then f := 1
else for i := 1 to n do
f := f*i
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите число элементов множества '); readln(n);
Factorial(n, f);
writeln('Десять человек могут находится в очереди ', f, ' способами')
end.
Пример 7. Сколько четных пятизначных чисел можно составить из цифр
2, 3, 4, 5, 9?
Математический алгоритм решения
Четными будут те числа, которые оканчиваются четной цифрой. В данном примере четных цифр две.
Допустим, что одна из четных цифр находится во всех случаях на последнем месте, тогда все получаемые числа будут четными. Сколько таких чисел будет? Их будет столько, сколько перестановок можно сделать из оставшихся 4-х цифр, т. е. 4! Но среди заданных цифр есть еще одна четная. Допустим, что теперь эта вторая цифра находится на последнем месте, тогда снова будут получаться четные числа и их также будет 4!
Окончательное число четных пятизначных чисел равно

Программу составить нетрудно. Выполните это самостоятельно.
Перестановки с повторениями
Пример 8. Сколько различных слов, каждое из которых состоит из семи букв, можно составить из букв слова "коробок".
В отличие от предыдущего примера здесь не все буквы слова различны (там были все цифры разными). Если бы все буквы были различны, то из них можно было бы составить 7! различных слов.
Однако не все перестановки букв дают новые слова. Очевидно, что перестановка букв "к", так же как и букв "о", между собой не дают нового слова. Следовательно, рассматриваемая задача свелась к тому, чтобы определить число перестановок, в результате которых получается одно и то же слово. Число перестановок буквы "к" между собой, в результате которых получаются одинаковые слова равно 2! После каждой такой перестановки буква "о" может быть переставлена 3! способами. Применяя правило произведения, получим, что каждое новое слово будет повторяться


Вообще, пусть дано множество M = {a, b, c, ...}, состоящее из n элементов, из которых элемент a повторяется n1 раз, элемент b - n2 раз, элемент c - n3 раз, ... так, что

Требуется найти число перестановок с заданным числом повторений входящих в него элементов.
Число перестановок в этом случае определяется по формуле:

где



Программа
Program Problem8;
uses WinCrt;
var
s, k1, k2 : longint;
{----------------------------------------------------------------------------------------}
Procedure Factorial(n : integer; var f : longint);
var
i : integer;
begin
f := 1;
if n = 0 then f := 1
else for i := 1 to n do f := f*i
end;
{----------------------------------------------------------------------------------------}
begin
Factorial(7, s); Factorial(3, k1); Factorial(2, k2);
s := s div (k1*k2);
writeln('Из слова "КОРОБОК" можно составить ', s, ' различных слов')
end.
Повторение
О рекурсии
1. Подпрограмме на Паскале (т.е. функции или процедуре) разрешено обращаться к самой себе - либо напрямую, либо через цепочку вызовов других подпрограмм, приводящую к первоначальной точке вызова.
О подпрограмме, которая вызывает саму себя, говорят, что она рекурсивна.
Многие математические функции и алгоритмы, будучи запрограммированы на Паскале, наиболее естественно выражаются именно в рекурсивной форме. В большинстве случаев рекурсивное решение задачи получается достаточно простым, но в то же время оказывается крайне неэффективным в сравнении с итеративной реализацией этого алгоритма.
2. Рекурсивное определение какого-либо понятия или процесса должно содержать два обязательных элемента: 1) условие прекращения рекурсии, задающее некоторое фиксированное значение для одного или нескольких простых этапов вычисления; 2) выражение более сложного этапа вычислений в терминах менее сложного. Правильно организованный рекурсивный процесс развивается таким образом, что любая сколь угодно сложная ситуация в конце концов сводится к условию прекращения рекурсии.
3. В качестве примера, демонстрирующего рекурсию, часто используют функцию факториала, определяемую как произведение всех натуральных чисел от 1 до n (в математической нотации n!). Например, 4! = 1 . 2 . 3 .
4 = 24. Этому вычислительному процессу можно придать и рекурсивную трактовку. Роль условия выхода из рекурсии здесь играет равенство 0! = 1 или 1! = 1. Выражение сложного этапа через более простой имеет вид n! = (n - 1)!

4. В подпрограмме на Паскале рекурсивный вызов внешне выглядит точно так же, как и вызов любой другой подпрограммы. Так, в функции fac, вычисляющей значение "n-факториал", ее тело имеет следующий вид:
if (n = 0) or (n = 1) then
fac := 1 {завершение рекурсии}
{иначе - рекурсивный вызов}
else fac := fac(n - 1)*n
Имя функции fac получает значение 1, если n равно 0 или 1; если же n больше единицы, то значение fac определяется как произведение n и значения, полученного от рекурсивного обращения к fac(n - 1).
Правила вычисления дисперсий и средних квадратических отклонений
1. Дисперсия постоянной величины равна нулю:
DC = 0, где C - постоянная.
2. При линейном преобразовании случайной величины X, т.е. для линейной функции
Y = kX + b,
дисперсия увеличивается в k раз, а среднее квадратическое отклонение - в |k|2 раз:
DY = D(KX + b) = k2 DX,
3. Теорема сложения дисперсий: если случайные величины X и Y независимы, то дисперсия и суммы равна сумме их дисперсий:
D(X + Y) = DX + DY,
и следовательно,

Следствие. Дисперсия линейной комбинации попарно независимых случайных величин X1, X2, ..., Xn может быть вычислена по формуле
D(C1X1
+ C2X2 + ... + CnXn) = C1
D2X1 + C2 D2X2 + ... + Cn D2Xn.
В частности, если все величины X1, X2, ..., Xn
имеют одинаковую дисперсию

то дисперсия их среднего арифметического равна

и, следовательно, среднее квадратическое отклонение равно

Предельная теорема Муавра-Лапласа
Если вероятность p наступления события A в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность P(X = m) того, что в n независимых испытаниях событие A наступит m раз, приближенно равна:

Значение функции Гаусса

Используя эти формулы можно составить процедуру вычисления вероятности по локальной формуле Муавра-Лапласа, но прежде составим функцию вычисляющую значение функции Гаусса:
{ Функция Гаусса }
Function G(x : real) : real;
begin
G := exp(-sqr(x)/2)/sqrt(2*Pi)
end;
Тогда процедура вычисления вероятности по локальной формуле Муавра-Лапласа будет следующей:
{ Процедура нахожд. вероятн. по локальной форм. Муавра-Лапласа }
Procedure Local_Laplace(n, m : longint; p : real; var pp : real);
var
x : real;
begin
x := (m - n*p)/sqrt(n*p*(1 - p));
pp := G(x)/sqrt(n*p*(1 - p))
end;
Пример 1. Вероятность того, что данное изделие будет забраковано, равна 0.2. Определить вероятность того, что в партии из 400 изделий будет 104 бракованных.
{ Использование локальной формулы Лапласа для вычисл. вероятн. }
Program Problem1;
uses WinCrt;
var
n, m : longint;
p, pp : real;
{----------------------------------------------------------------------------------------}
{ Функция Гаусса }
Function G(x : real) : real;
begin
G := exp(-sqr(x)/2)/sqrt(2*Pi)
end;
{----------------------------------------------------------------------------------------}
{ Процедура нахожд. вероятн. по локальной форм. Муавра-Лапласа }
Procedure Local_Laplace(n, m : longint; p : real; var pp : real);
var
x : real;
begin
x := (m - n*p)/sqrt(n*p*(1 - p));
pp := G(x)/sqrt(n*p*(1 - p))
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите число изделий в партии '); readln(n);
write(' Введите вероятность быть бракованным для одного ');
write('изделия '); readln(p);
write('Введите число изделий, вероятность которых надо ');
write('найти '); readln(m);
Local_Laplace(n, m, p, pp);
writeln('Вероятность появления ', m, ' бракованных');
writeln('изделий среди ', n, ' изделий равна ', pp:1:6)
end.
Пример 2. Появление бракованного изделия в партии оценивается вероятностью 0.5. Взято 100 изделий. Какова должна быть частота бракованных изделий, чтобы вероятность такой частоты была бы равна 0.0782?
{ Использование локальной формулы Лапласа для вычисл. вероятн. }
Program Problem2;
uses WinCrt;
var
n, m : longint;
p, Pm : real;
{----------------------------------------------------------------------------------------}
{ Функция Гаусса }
Function G(x : real) : real;
begin
G := exp(-sqr(x)/2)/sqrt(2*Pi)
end;
{----------------------------------------------------------------------------------------}
{ Процедура определения частоты. 1-й способ. }
Procedure
Frequency1(n : longint; p, Pm : real;
var
m : longint);
var
x, pp : real;
begin
m := -1;
repeat
m := m + 1;
x := (m - n*p)/sqrt(n*p*(1 - p));
pp := G(x)/sqrt(n*p*(1 - p))
until pp >= Pm
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите общее число изделий в партии '); readln(n);
write('Введите вероятность быть бракованным для одного ');
write('изделия '); readln(p);
write('Введите вероятность получения частоты '); readln(Pm);
Frequency1(n, p, Pm, m);
writeln('Частота бракованных изделий равна ', m)
end.
Пример 3. По данным длительной проверки качества выпускаемых запчастей брак составляет 13%. Определить вероятность того, что в непроверенной партии из 200 запчастей пригодных будет а) 174; б) от 150 до 180.
Program Problem3a;
uses WinCrt;
var
n, m : longint;
p, q, pp : real;
{----------------------------------------------------------------------------------------}
{ Функция Гаусса }
Function G(x : real) : real;
begin
G := exp(-sqr(x)/2)/sqrt(2*Pi)
end;
{----------------------------------------------------------------------------------------}
{ Локальная формула Муавра-Лапласа }
Procedure Local_Laplace(n, m : longint; p : real; var pp : real);
var
x : real;
begin
x := (m - n*p)/sqrt(n*p*(1 - p));
pp := G(x)/sqrt(n*p*(1 - p))
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите число запчастей в партии '); readln(n);
write(' Введите вероятность быть бракованным для одной запчасти ');
readln(q);
write('Введите число запчастей, вероятность которых надо ');
write('найти '); readln(m);
p := 1 - q;
Local_Laplace(n, m, p, pp);
writeln('Вероятность появления ', m, ' пригодных');
writeln('запчастей среди ', n, ' изделий равна ', pp:1:6)
end.
Преобразование типов
Пример 8. Двузначное десятичное число в сумме с числом, записанным теми же цифрами, но в обратном порядке, дает полный квадрат. Найти все такие числа.
Пусть искомое двузначное число




Сумма этих чисел должна давать полный квадрат, т.е. точный квадрат целых чисел. Как это проверить?
Проверку можно было бы выполнить так: извлечь квадратный корень из полученной суммы; затем округлить результат до целого числа, а потом умножить полученный результат на себя, если снова получится сумма этих чисел, то значит она является точным или полным квадратом.
Например, 12 + 21=33, извлекаем квадратный корень из 33, он равен 5.74...; округляем, будет 6; умножаем 6 само на себя и получаем 36.
Мы не получили исходного результата, значит сумма 33 не является точным квадратом.
Еще один пример, чтобы вам была понятна идея решения. Пусть двузначное число 29, тогда число, записанное теми же цифрами, но в обратном порядке - 92, в сумме они дают 121. Извлекаем квадратный корень из 121 и получаем 11. Умножив 11 само на себя, снова получим 121. Делаем вывод, что получен точный квадрат, а значит двузначное число 29 является искомым.
Чтобы составить программу по этому принципу, придется извлекать квадратный корень из суммы, что можно сделать с помощью стандартной функции sqrt(x). Результат функции sqrt(x) является вещественным числом, его надо округлить или отбросить дробную часть, а нам неизвестно, как это сделать.
Но, даже более существенным, является то, что если квадратный корень в множестве целых чисел извлекается нацело, как для 121 (он равен 11), то на множестве вещественных чисел мы не получим строго число 11, а результат будет очень близок к 11 и после умножения на себя всё равно не получится 121, т.е. возникает необходимость преобразовать
вещественное значение в целое.
Итак перед нами две задачи: 1) выяснить как округлять числа и; 2) установить, как преобразовывать вещественный тип в целый.
Для этого в Паскале есть стандартные функции round(x) и trunc(x)
Стандартные функции round и trunc предназначены для замены значений вещественного типа значениями целого типа.
Функция round(x) округляет вещественное число x до целого - ее значение есть ближайшее целое число:
round(4.2) = 4, round(4.7) = 5, round(4.5)=5,
round(-4.2) = -4, round(-4.7) = -5, round(-4.5) = -5.
Функция trunc(x) отбрасывает (без округления) дробную часть вещественного числа x:
trunc(1.2) = 1, trunc(5.8) = 5, trunc(-1.2) = -1,
trunc(-5.8) = -5, trunc(-6.7) = -6, trunc(8,9) = 8
Функции округления связаны так:
trunc(x + 0.5) = round(x), если x

trunc(x - 0.5) = round(x), если x < 0.
Итак, в программе можно воспользоваться одной из этих функций. Какой? Подумайте сами и попробуйте применить в программе вначале функцию trunc, а потом замените ее на round и сравните полученные результаты.
Программа
Program Problem8;
uses WinCrt;
var
d, e, k : integer;
begin
writeln('Искомые двузначные числа');
for d := 1 to 9 do
for e := 1 to 9 do
begin
k := round(sqrt(d*10 + e + e*10 + d));
if k*k = d*10 + e + e*10 + d
then write(d*10 + e, ' ')
end
end.
Задание 7
Найти целые числа из заданного промежутка [m; n], которые являются точными квадратами и остаются таковыми после приписывания к ним справа единицы (в десятичной системе записи).
Упражнения
37. Составьте программу, которая находит 4 последовательных натуральных числа, произведение которых равно 1680.
38. Показать, что четырехзначное число, у которого цифры тысяч и десятков одинаковы и цифры сотен и единиц тоже одинаковы, не может быть точным квадратом.
39. Произведение шести последовательных натуральных чисел может быть равно произведению трех последовательных натуральных чисел. Например, 1







40. Доказать, что произведение четырех последовательных целых чисел в сумме с единицей дает полный квадрат.
41. Найдите 11 последовательных натуральных чисел, сумма квадратов которых есть квадрат целого числа.
42. Существуют ли такие целые числа, которые уменьшаются в 57 раз при зачеркивании их первой (слева) цифры?
43. Найти четырехзначное число, зная, что оно является квадратом натурального числа и что цифры его распадаются на две пары, состоящие из одинаковых цифр.
44. Найдите все семизначные числа, которые делятся на 15 и записываются только цифрами 0 и 1.
45. Шестизначное число начинается с цифры 1. Если эту цифру переставить в конец числа, то новое число будет в три раза больше первоначального. Найдите число.
46. Сколько точных квадратов можно составить из цифр 3, 4, 5, 6?
47. Даны 20 различных натуральных чисел, не больших 50. Найдите два из них, разность которых равна 4, 5 или 9.
48. Во сколько раз увеличится двузначное число, если справа к нему приписать такое же двузначное число?
49. Определить наибольшее значение отношения трехзначного числа к числу, равному сумме цифр этого числа.
50. Найти трёхзначное число, кратное 45, если разность между этим числом и числом, записанным теми же цифрами, но в обратном порядке равна 297.
51. Найти четырёхзначное число


52. Найти трёхзначное число, равное сумме цифры десятков, квадрата цифры сотен и куба цифры единиц.
53. Найти два числа, произведение которых есть трёхзначное число, являющееся кубом некоторого числа, а частное является квадратом этого числа.
54. Разность между числом и произведением его цифр равна сумме цифр этого числа. Найти это число.
55. Найти все значения числа m, для которых сумма 1! + 2! + ,,, + m! является полным квадратом.
56. Найти положительное четырёхзначное число, кратное 7 и представляющее собою сумму куба и квадрата некоторого числа.
57. Некоторое число при делении на 7 дает в остатке 3; его квадрат при делении на 72 дает остаток 44; его куб при делении на 73
даёт остаток 111. Найти это число.
58. При каком натуральном значении a число a2 + a + 1589 будет точным квадратом?
59. Найти совершенное число вида 16p.
60. Найти два числа, если сумма их квадратов равна 468, а сумма их общего наибольшего делителя и наименьшего кратного равна 42.
Ответы
К заданию 1
Program
Task1;
uses WinCrt;
var
n, f, i, s : longint;
begin
write('Введите натуральное число '); readln(n);
s := 0; f := 1;
for i := 1 to n do
begin
f := f*i; s := s + f
end;
writeln('Сумма факториалов чисел от 1 до ', n, ' равна ', s)
end.
К
заданию 4
Program Task4;
uses WinCrt;
var
t, s, d, e : integer;
begin
writeln('Искомое четырехзначное число');
for t := 1 to 9 do
for s := 0 to 9 do if s <> t then
for d := 0 to 9 do if (d <> s) and (d <> t) then
for e := 0 to 9 do
if (e <> d) and (e <> s) and
(e <> t) then
if (t*1000 + s*100 + d*10 + e)*9 = t*10000 + s*100 + d*10 + e
then writeln(t*1000 + s*100 + d*10 + e)
end.
К
заданию 6
Program Task6;
uses WinCrt;
var
x, y, z, n, k, p : longint;
begin
write('Введите натуральное число '); readln(n);
k := 0; x := 1;
while x*x + 2<=n do
begin
k := k + 1; x := x + 1
end;
p := 0;
for x := 1 to k do
for y := 1 to x do
for z := 1 to y do
if x*x + y*y + z*z=n
then
begin
p := p + 1;
writeln(x, '*', x, '+', y, '*', y, '+', z, '*', z, '=', n)
end;
if
p=0
then
begin
write('Число ', n, ' нельзя представить в виде ');
writeln(' суммы квадратов трех чисел')
end
else
writeln('Число способов равно ', p)
end.
К
заданию 7
Program Task7;
uses WinCrt;
var
m, n, i, k, k1 : longint;
begin
write('Введите начало промежутка '); readln(m);
write('Введите конец промежутка '); readln(n);
write('Искомые числа ');
for i := m to n do
begin
k := round(sqrt(i));
k1 := round(sqrt(i*10 + 1));
if (k*k = i) and (k1*k1 = i*10 + 1) then
write(i, ' ')
end
end.
Приближенное вычисление интегралов
Пусть требуется вычислить определенный интеграл

На этом занятии мы познакомимся с простыми способами приближенного вычисления: формулой прямоугольников, формулой трапеций, формулой Симпсона или параболическим интегрированием, методом Монте-Карло.
3.1. Формула прямоугольников
Будем исходить из геометрических соображений и рассматривать определенный интеграл

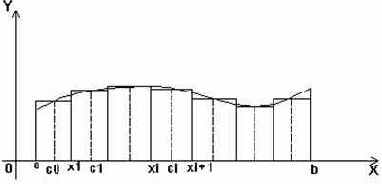
Рис. 48
Идея, которая привела к понятию определенного интеграла заключалась в следующем. Разбить всю фигуру на полоски одинаковой ширины dx = (b - a)/n, а затем каждую полоску заменить прямоугольником, высота которого равно какой-либо ординате (см. рис. 48).
Тогда получится следующая формула:

где xi
<= ci <= xi+1 (i = 0, 1, ..., n-1). Площадь криволинейной фигуры заменится площадью сумм прямоугольников. Эта приближенная формула и называется формулой прямоугольников.
Практически, в качестве точки ci берут середину промежутка [xi , xi+1], т. е.

Нетрудно составить процедуру вычисления такой суммы.
{ Вычисление интеграла методом прямоугольников }
{ Rectangle - прямоугольник }
Procedure Rectangle(a, b : real; n : integer; var j : real);
var
dx, c, f : real;
i : integer;
begin
dx := (b - a)/n;
c := a + dx/2;
f := fx(c);
for i := 1 to n - 1 do
begin
c := c + dx;
f := f + fx(c)
end;
j := dx * f
end;
Теперь возникает вопрос о числе точек деления - n, который напрямую связан с точностью вычисления интеграла.
Известно, что точность вычисления интеграла по формуле прямоугольников оценивается по дополнительному члену, который выражается формулой:


значит оценивать точность вычисления можно по модулю этого остаточного или дополнительного члена, |Rn|.
Вторую производную вычислить мы сможем с достаточно высокой степенью точности, применив следующую функцию:
{ Функция вычисления второй производной }
Function
derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
Осталось выяснить, в какой точке промежутка интегрирования [a, b] находить значение этой производной. Остаточный член не требует строго определенного значения аргумента из этого промежутка, поэтому можно выбрать любое значение, не выходящее за пределы интервала [a, b]. Сразу возникает мысль вычислить вторую производную в середине промежутка, т.е. в точке (a + b)/2. Но представьте себе ситуацию, когда промежуток [-1, 1] или [-6.28; 6.28], тогда середина этого отрезка - точка 0 и значение производной будет равно нулю, а значит для числа точек деления n может быть установлено значение любое, даже 1, что, конечно, не даст требуемой точности вычисления интеграла.
Итак, следующая проблема, в какой точке промежутка находить значение производной?
Можно найти наибольшее значение производной на промежутке интегрирования [a, b]. Это можно сделать с помощью процедуры:
{ Определение наибольшего значения второй производной }
Procedure Maximum(a, b, eps : real; var
max : real);
var
dx, x : real;
begin
dx := 0.1; x := a;
max := abs(derivat2(x, eps));
while x<= b do
begin
x := x + dx;
if max < abs(derivat2(x, eps))
then max := abs(derivat2(x, eps))
end
end;
В ней установлен шаг - 0.1 и затем, в каждой следующей точке промежутка определяется значение второй производной и находится наибольшее.
Теперь составим процедуру определения числа точек деления, а затем и полностью программу.
{ Процедура определения числа точек деления промежутка интегр. }
Procedure Number(a, b, eps, max : real; var
n : integer);
var
d : real;
begin
n := 1;
d := abs((b - a)*(b - a)*(b - a));
while (max*d)/(24*n*n) >= eps do n := n+1;
end;
Программа вычисления интеграла по формуле прямоугольников
{ Вычисление интеграла по формуле прямоугольников }
Program Jntegral_Rectangle2;
uses WinCrt;
var
a, b, eps, j : real;
n : integer;
{----------------------------------------------------------------------------------------}
Function fx(x : real) : real;
begin
fx := sin(x)
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления второй производной }
Function derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
{----------------------------------------------------------------------------------------}
{ Процедура определения числа точек деления промежутка интегр. }
Procedure Number(a, b, eps : real; var
n : integer);
var
dy2, d, c, dx : real;
begin
c := (a + b)/2;
dy2 := derivat2(c, eps);
if dy2 = 0
then
begin
c := a; dx := (b - a)/10;
while derivat2(c, eps) = 0 do c := c + dx;
dy2 := derivat2(c, eps)
end;
n := 1;
d := abs((b - a)*(b - a)*(b - a));
while abs(dy2*d)/(24*n*n) >= eps do n := n+1;
end;
{----------------------------------------------------------------------------------------}
{ Вычисление интеграла методом прямоугольников }
Procedure Rectangle(a, b : real; n : integer; var j : real);
var
dx, c, f : real;
i : integer;
begin
dx := (b - a)/n;
c := a + dx/2;
f := fx(c);
for i := 1 to n - 1 do
begin
c := c + dx;
f := f + fx(c)
end;
j := dx * f
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите нижний предел интегрирования '); readln(a);
write('Введите верхний предел интегрирования '); readln(b);
write('Введите точность вычисления интеграла '); readln(eps);
Number(a, b, eps, n); Rectangle(a, b, n, j);
writeln('Значение интеграла равно ', j:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
Такой способ можно использовать, но он может быть долгим, особенно, если большой промежуток интегрирования, малый шаг и более высокая точность вычисления производной.
Для определения числа точек деления можно применить и другой прием.
{ Процедура определения числа точек деления промежутка интегр. }
Procedure Number(a, b, eps : real; var
n : integer);
var
dy2, d, c, dx : real;
begin
c := (a + b)/2;
dy2 := derivat2(c, eps);
dx := (b - a)/10;
if dy2 = 0
then
begin
c := a;
while derivat2(c, eps) = 0 do c := c + dx;
dy2 := derivat2(c, eps)
end;
n := 1;
d := abs((b - a)*(b - a)*(b - a));
while abs(dy2*d)/(24*n*n) >= eps do n := n+1;
end;
Как работает эта процедура? Вычисляется значение второй производной в середине промежутка: c := (a + b)/2. Если она не равна нулю, тогда все в порядке, вычисляется в зависимости от заданной точности число точек деления n. Если значение второй производной равно нулю в середине промежутка интегрирования: dy2 = 0, тогда устанавливается шаг dx := (b - a)/10 и начинается цикл, в котором вычисляется производная через каждый промежуток dx, начиная от точки a, пока производная равна нулю цикл продолжается и заканчивается как только она не станет равной нулю.
Такой прием экономит время работы программы, производную можно вычислить с большей точностью, да и сама программа становится менее громоздкой:
Program Jntegral_Rectangle2;
uses WinCrt;
var
a, b, eps, j : real;
n : integer;
Function fx(x : real) : real;
begin
fx := sin(x)
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления второй производной }
Function derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
{----------------------------------------------------------------------------------------}
{ Процедура определения числа точек деления промежутка интегр. }
Procedure Number(a, b, eps : real; var
n : integer);
var
dy2, d, c, dx : real;
begin
c := (a + b)/2;
dy2 := derivat2(c, eps);
if dy2 = 0
then
begin
c := a; dx := (b - a)/10;
while derivat2(c, eps) = 0 do c := c + dx;
dy2 := derivat2(c, eps)
end;
n := 1;
d := abs((b - a)*(b - a)*(b - a));
while abs(dy2*d)/(24*n*n) >= eps do n := n+1;
end;
{----------------------------------------------------------------------------------------}
{ Вычисление интеграла методом прямоугольников }
Procedure Rectangle(a, b : real; n : integer; var j : real);
var
dx, c, f : real;
i : integer;
begin
dx := (b - a)/n;
c := a + dx/2;
f := fx(c);
for i := 1 to n - 1 do
begin
c := c + dx;
f := f + fx(c)
end;
j := dx * f
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите нижний предел интегрирования '); readln(a);
write('Введите верхний предел интегрирования '); readln(b);
write('Введите точность вычисления интеграла ');
readln(eps);
Number(a, b, eps, n);
Rectangle(a, b, n, j);
writeln('Значение интеграла равно ', j:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
3.2. Формула трапеций
Рис. 49
Заменим данную кривую вписанной в нее ломаной, с вершинами в точках (xi, yi), где yi = f(xi) (i = 0, 1, 2, ..., n-1). Тогда криволинейная трапеция заменится фигурой, состоящей из трапеций (см. рис. 49). Будем по-прежнему считать, что промежуток [a, b] разбит на равные части, тогда площади этих трапеций будут равны:

Складывая полученные значения, приходим к приближенной формуле:

Эта приближенная формула называется формулой трапеций.
Оценка погрешности формулы трапеций определяется по следующему дополнительному члену:


Задание 4
Составьте процедуры вычисления интеграла по формуле трапеций и процедуру определения числа точек деления.
Составьте полностью программу и вычислите интегралы следующих функций на указанных промежутках с заданной точностью:
1) f(x) = 1/x на [1; 2] с точностью до 0.001;
2) f(x) = x/(x2
+ 1)2 на [-1; 2] с точностью до 0.01;
3) f(x) = 1/cos2 x на [0; Pi/3] с точностью до 0.0000001.
3.3. Параболическое интерполирование. Дробление промежутка интегрирования. Формула Симпсона
Параболическое интерполирование
Для приближенного вычисления интеграла функции



и тогда будет выполняться приближенное равенство

Такая замена тем более важна, когда подынтегральная функция представляет собой выражение, интеграл которой точно вычислить нельзя.
Геометрически это можно представить так, что криволинейная трапеция, находящаяся под кривой y = f(x) заменяется "параболой k-го порядка", поэтому такой процесс получил название параболическое интерполирование.
Существует много интерполяционных многочленов, о некоторых из них мы будем говорить на других занятиях, а на этом познакомимся с интерполяционным многочленом Лагранжа, который строится по следующей формуле:


При интегрировании получается линейное относительно значений

При k = 0, функция f(x) просто заменяется постоянной f(c0), где c0 - любая точка из промежутка [a, b], например средняя: c0 = (a + b)/2. Тогда приближенно

Геометрически это означает, что криволинейная фигура под кривой y = f(x) заменяется прямоугольником с высотой, равной средней ординате.
При k = 1 функция f(x) заменяется линейной функцией P1(x), которая имеет одинаковые с ней значения при x = c0 и x = c1. Если взять c0
= a, c1 = b, то

после преобразования, получим

Таким образом, здесь мы приближенно допускаем

Геометрически это будет представляться, как замена криволинейной фигуры трапецией: вместо кривой берется хорда, соединяющая ее концы.
Более интересный результат получается, если взять k = 2. Можно положить c0= a, c1 = (a + b)/2, c2 = b, тогда интерполяционный многочлен P2(x), будет иметь вид


После преобразований и интегрирования многочлена P2(x), приходим к приближенной формуле

В этом случае, площадь фигуры под кривой заменяется площадью фигуры, ограниченной параболой (с вертикальной осью), проходящей через крайние и среднюю точки кривой.
Увеличивая степень k интерполяционного многочлена, т.е. проводя параболу через все большее число точек данной кривой, можно добиться большей точности. Но на практике часто используют другой способ, основанный на сочетании параболического интерполирования с идеей дробления промежутка.
3.4. Дробление промежутка интегрирования
Для вычисления интеграла

[x0, x1], [x1, x2], ..., [xn-1, xn] (x0 = a, xn = b),
искомый интеграл представится в виде суммы

После этого, к каждому из этих промежутков применим параболическое интерполирование, т.е. станем вычислять перечисленные интегралы по одной из приближенных формул: прямоугольников, трапеций или по параболической формуле (7).
В первых двух случаях мы получим уже известные формулы прямоугольников и трапеций.
Применим теперь формулу (7) к каждому из интегралов, при этом положим, что



Получим


................................................

Складывая почленно эти равенства, получим формулу:

Эта формула называется формулой Симпсона. Ею пользуются для приближенного вычисления интегралов чаще, чем формулами прямоугольников и трапеций, так как она дает более точный результат.
Составим процедуру на языке Паскаль реализующую эту формулу.
{ Вычисление интеграла по формуле Симпсона }
Procedure Simpson(a, b : real; n : integer; var j : real);
var
dx, c, c1, f : real;
i : integer;
begin
dx := (b - a)/n;
c := a;
c1 := a + dx/2;
f := fx(a) + fx(b) + 4*fx(c1);
for i := 1 to n - 1 do
begin
c := c + dx; c1 := c1 + dx;
f := f + 2*fx(c) + 4*fx(c1)
end;
j := (dx/6)* f
end;
Остается выяснить вопрос о числе точек деления в зависимости от заданной точности вычисления, другими словами, установить погрешность вычисления.
Если промежуток [a, b] разделен на n равных частей, то для формулы Симпсона дополнительный член имеет вид


Значит оценить точность вычисления можно по модулю этого дополнительного члена: |Rn|.
Однако, это связано с неприятностью находить 4-ю производную функции, что достаточно нелегкое дело. Есть и другой путь оценки точности вычисления интегралов и не только по формуле Симпсона, но и по формуле прямоугольника и трапеций.
Этот прием заключается в следующем. Искомый интеграл вычисляется дважды: при делении отрезка [a, b] на n частей и на 2n частей. Полученные значения интегралов In
и I2n сравниваются и первые совпадающие десятичные знаки считаются верными.
Покажем, как, используя такой метод оценить точность интеграла, вычисленного по формуле Симпсона.
Преобразуем дополнительный член Rn формулы Симпсона:

Пусть Rn
и R2n - погрешности интегрирования, тогда, учитывая предыдущую формулу можно составить пропорцию:

Понятно, что h2n
= hn/2. Тогда из пропорции получаем: Rn = 16 R2n. Если I - истинное значение интеграла, то I = In + Rn и I = I2n + R2n, откуда находим: In + 16 R2n
= I2n + R2n, т.е.

Надо помнить, что в процессе практических вычислений при последовательном удвоении числа отрезков разбиения начинает сильно прогрессировать удельный вес ошибки округления, значение которой с некоторого момента ставит предел достижимой точности.
Ниже, мы рассмотрим и другой способ оценки точности. А сейчас, основываясь на последней формуле, составим программу вычисления интеграла с применением формулы Симпсона.
{ Вычисление интеграла по формуле Симпсона }
Program Jntegral_Simpson;
uses WinCrt;
var
a, b, eps, j, j1 : real;
n : integer;
Function fx(x : real) : real;
begin
fx := exp(-x*x)
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Вычисление интеграла по формуле Симпсона }
Procedure Simpson(a, b : real; n : integer; var j : real);
var
dx, c, c1, f : real;
i : integer;
begin
dx := (b - a)/n;
c := a;
c1 := a + dx/2;
f := fx(a) + fx(b) + 4*fx(c1);
for i := 1 to n - 1 do
begin
c := c + dx; c1 := c1 + dx;
f := f + 2*fx(c) + 4*fx(c1)
end;
j := (dx/6)* f
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите нижний предел интегрирования '); readln(a);
write('Введите верхний предел интегрирования '); readln(b);
write('Введите точность вычисления интеграла '); readln(eps);
n := 2;
Simpson(a, b, n, j); Simpson(a, b, 2*n, j1);
while abs(j - j1)/15 > eps do
begin
n := n + 2;
Simpson(a, b, n, j); Simpson(a, b, 2*n, j1)
end;
writeln('Значение интеграла равно ', j1:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
3.5. Об оценке погрешности
При вычисление интегралов по формуле прямоугольников и по формуле трапеций оценка погрешности делалась по формуле с помощью второй производной, которая была ограничена на заданном промежутке своим наибольшим значением.
Так, в формуле трапеций, оценка погрешности использовалась для определения числа точек разбиения, которое определяло точность вычисления. Это делалось с помощью процедуры:
{ Процедура определения числа точек деления промежутка интегр. }
Procedure Number(a, b, eps, max : real; var
n : integer);
var
d : real;
begin
n := 1;
d := abs((b - a)*(b - a)*(b - a));
while (max*d)/(24*n*n) >= eps do n := n+1;
end;
Такого рода оценки погрешности называются гарантированными оценками погрешности.
На основании этой оценки можно гарантировать, что погрешность приближенного значения интеграла не превосходит определенной величины.
Существует второй способ оценки - отказ от получения строгой, гарантированной оценки погрешности и получение оценки погрешности лишь с определенной степенью достоверности. В частности при оценки погрешности вычисления интеграла по методу Симпсона погрешность оценивалась через разность результатов приближенного значения интеграла при различных значениях параметров, в частности, при n и 2n.
Необходимость применения метода Симпсона, как раз по причине метода оценки погрешности, примененной в этом методе, в следующих случаях.
1) Когда уже первая производная подынтегральной функции равна нулю.
2) Когда первая производная подынтегральной функции обращается в точках (пределах интегрирования или других) в бесконечность.
Примером может быть интеграл

Подынтегральная функция при

Эти два обстоятельства вызывают необходимость выбирать метод интегрирования в зависимости от заданной функции и поведения ее производных.
Задание 5
1. Используя оператор выбора Case ... of ..., составьте программу, с помощью которой пользователю можно было бы выбирать метод интегрирования, подобно программе выбора метода решения уравнений.
2. Вычислите по формуле Симпсона следующие интегралы:
1) полный эллиптический интеграл 2-го рода

2)


3.6. Вычисление интегралов методом Монте-Карло
Вычисление интегралов методом Монте-Карло часто применяется для двойных, тройных, вообще, кратных интегралов. Идея метода состоит в следующем.
Пусть задана некоторая подынтегральная функция F - непрерывная в области интегрирования Q. Выберем в этой области n случайных точек M, найдем значение заданной функции в некоторой "средней" точке области интегрирования. При достаточно большом n можно считать, что

Тогда, значение интеграла приблизительно равно

Применим этот метод для простейшего интеграла на промежутке [a, b], т.е. необходимо вычислить интеграл:

В этом случае в качестве объема области интегрирования D выступает длина отрезка [a, b], которая равна: D = b - a.
Пусть xi (i = 1, 2, ..., n) - случайные точки из промежутка [a, b], тогда значение функции f(x) в некоторой "средней" точке будет:

а значение интеграла станет равно

Для получение точек xi можно использовать уже известный способ нахождения случайных точек с помощью функции random,
x := random*(b - a) + a
Функция для вычисления интеграла получится такой:
{ Функция вычисления интеграла методом Монте-Карло }
Function I(n : longint; a, b : real) : real;
var
x, f : real;
k : longint;
begin
randomize;
f := 0;
for k := 1 to n do
begin
x := random*(b - a) + a;
f := f + fx(x)
end;
I := (b - a)*f/n
end;
Итак, с помощью генератора случайных чисел (random) вырабатывается случайное число из промежутка [a, b], находится значение функции в этой точке и суммируются ее абсолютные величины (учитывая, что функция может принимать и отрицательные значения) в переменную f. Приближенное значение интеграла вычисляется с помощью оператора I := (b - a)*f/n.
Теперь стоит очень болезненный вопрос оценки точности значения интеграла. Не вдаваясь в долгие математические рассуждения (о чем смотрите [19]), покажем неравенства, с помощью которых можно оценить точность вычисления интеграла.
Пусть I(f) - точное значение интеграла, а Sn(f) - его приближенное значение, тогда с вероятностью 0,997 и 0,99999 выполняются следующие соотношения


Здесь D(f) - дисперсия непрерывной случайной величины, которая вычисляется по формуле:

где сумма есть математическое ожидание случайной величины.
Приведем схему последовательного вычисления интеграла с заданной точностью eps. Последовательно, при n = 1, ... получаются случайные точки x и вычисляющая величины tn
, Sn , dn , пользуясь рекуррентными соотношениями




и величину


Начальные условия рекурсии n = 1,



Если оказалось, что


Изложенные математические соображения можно реализовать следующей процедурой:
{ Процедура оценки точности и вычисления интеграла }
Procedure Monte_Karlo(a, b, eps : real; var
s : real);
var
t, d, f, dd : real;
n : longint;
begin
n := 1;
t := I(n, a, b);
s := t;
d :=0;
repeat
n := n + 1;
t := t + I(n, a, b);
s := t/n;
d := d + (n/(n - 1))*sqr(I(n, a, b) - s);
dd := d/(n - 1)
until 5*sqrt(dd/n) < eps
end;
Полностью программа приводится ниже. Надо заметить, что для интегралов на промежутке программа работает медленно и лучше применять для их вычисления другие методы, а вот для кратных интегралов программа может быть очень полезной.
{Вычисление интеграла и оценка его точности методом Монте-Карло}
Program Integral_Monte_Karlo;
uses WinCrt;
var
a, b, s, eps : real;
{-----------------------------------------------------------------------------------------}
Function fx(x : real) : real; { Промежуток интегрир. [3, 4] }
begin { Интеграл хорошо вычисл. с точн. до 0.00001 }
fx := sin(0.2*x - 3)/(x*x + 1)
end;
{-----------------------------------------------------------------------------------------}
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления интеграла методом Монте-Карло }
Function I(n : longint; a, b : real) : real;
var
x, f : real;
k : longint;
begin
randomize;
f := 0;
for k := 1 to n do
begin
x := random*(b - a) + a;
f := f + fx(x)
end;
I := (b - a)*f/n
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления точности и интеграла }
Procedure Monte_Karlo(a, b, eps : real; var s : real);
var
t, d, f, dd : real;
n : longint;
begin
n := 1;
t := I(n, a, b);
s := t;
d :=0;
repeat
n := n + 1;
t := t + I(n, a, b);
s := t/n;
d := d + (n/(n - 1))*sqr(I(n, a, b) - s);
dd := d/(n - 1)
until 5*sqrt(dd/n) < eps
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
randomize;
write('Введите нижний предел интегрирования '); readln(a);
write('Введите верхний предел интегрирования '); readln(b);
write('Введите точность вычисления '); readln(eps);
Monte_Karlo(a, b, eps, s);
writeln('Значение интеграла равно ', s:6:t(eps));
write('С точностью до ', eps:1:t(eps));
writeln(' и вероятностью 0.99999')
end.
Задание 6
Используя второй способ оценки погрешности через разность результатов приближенного значения интеграла при различных значениях аргументов, изменить программу вычисления интеграла по методу Монте-Карло. И вычислить с ее помощью интегралы из задания 5.
3.7. Вычисление двойных интегралов методом Монте-Карло
Вначале сделаем отступление в курс математического анализа и познакомимся с понятием двойного интеграла. Как и прежде, в определении понятий математического анализа, мы будем следовать Г.М. Фихтенгольцу.
Возникновение двойного (определенного) интеграла связывают с задачей определения объема цилиндрического бруса, подобно тому, как определенный интеграл возник из задачи определения площади криволинейной трапеции.
Рассмотрим тело (V), которое сверху ограничено поверхностью z = f(x, y), с боков - цилиндрической поверхностью с образующими, параллельными оси z, наконец, снизу - плоской фигурой (P) на плоскости xy. Требуется найти объем V тела.
Для решения этой задачи мы прибегаем к обычному в интегральном исчислении приему, состоящему в разложении искомой величины на элементарные части, приближенному подсчету каждой части, суммированию и последующему предельному переходу. С этой целью разложим область (P) сетью кривых на части (P1), (P2), ..., (Pn) и рассмотрим ряд цилиндрических столбиков, которые имеют своими основаниями эти частичные области и в совокупности составляют данное тело.
Для подсчета объема отдельных столбиков возьмем произвольно в каждой фигуре (Pi) по точке (xi, yi). Если приближенно принять каждый столбик, за настоящий цилиндр с высотой, равной аппликате f(xi, yi), то объем отдельного столбика оказывается приближенно равным f(xi, yi)*Pi, где Pi означает площадь фигуры (Pi). В таком случае приближенное выражение объема всего тела будет

Для повышения точности этого равенства будем уменьшать размеры площадок (Pi), увеличивая их число. В пределе, при стремлении к нулю наибольшего из диаметров всех областей (Pi), это равенство делается точным, так что

и поставленная задача решена.
Предел этого вида и есть двойной интеграл от функции f(x, y) по области (P); он обозначается символом


Таким образом, двойной интеграл является прямым обобщением понятия простого определенного интеграла на случай функции двух переменных.
Пример 1. Вычислить интеграл, распространенный на прямоугольник
(P) = [3, 4; 1, 2]:

Решить этот интеграл методом Монте-Карло очень просто. Для этого достаточно изменить функцию:
Function fx(x, y : real) : real;
begin
fx := 5*x*x*y - 2*y*y*y
end;
Изменить функцию вычисления интеграла, куда добавить в качестве входных параметров две другие координаты прямоугольной области по оси OY и в результате вычисления умножать среднее значение функции, не на длину отрезка, а на площадь области, в данном случае, на площадь прямоугольника. Разумеется, задавать случайные значения для y из соответствующего промежутка [a1, b1].
Функция станет такой:
{ Функция вычисления интеграла методом Монте-Карло }
Function I(n : longint; a, b, a1, b1 : real) : real;
var
x, y, f : real;
k : longint;
begin
randomize;
f := 0;
for k := 1 to n do
begin
y := random*(b1 - a1) + a1;
x := random*(b - a) + a;
f := f + fx(x, y)
end;
I := (b - a)*(b1 - a1)*f/n
end;
Необходимо внести незначительные изменения в процедуру Monte_Karlo, а в основной программа, не забыть описать новые переменный и ввести их в программу.
Составьте программу самостоятельно и выполните ее.
Задание 7
Вычислить двойной интеграл

где (P) есть круг радиуса R с центром в начале координат.
Библиотека часто встречающихся процедур и функций
43. Процедура уточнения корня методом хорд.
{ Процедура уточнения корня методом хорд }
Procedure chord(a, b, eps, min : real; var
x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - ((b - x1)*fx(x1))/(fx(b) - fx(x1));
x1 := x
until abs(fx(x))/min < eps
end;
44. Функция вычисления первой производной.
{ Вычисление 1-й производной и опред. точности ее вычислен.}
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs(dy2/(2*dx)) < eps;
derivat1 := dy/dx
end;
45. Процедура определения наименьшего значения первой производной.
{ Процедура определения наименьшего значения производной }
{ на заданном промежутке }
Procedure minimum(a, b, eps : real; var min : real);
var
d : real;
begin
a := a - eps;
b := b + eps;
repeat
a := a + eps;
b := b - eps;
min := abs(derivat1(a, eps));
d := abs(derivat1(b, eps));
if min > d then min := d
until min <> 0
end;
46. Функция вычисления порядка, в зависимости от задаваемой точности.
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
47. Процедура уточнения корня методом касательных.
{ Процедура уточнения корня методом касательных }
Procedure tangent(a, b, eps, min, dy : real; var x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - fx(x1)/derivat1(x1);
x1 := x
until abs(fx(x))/min < eps
end;
48. Функция вычисления второй производной.
{ Функция вычисления второй производной }
Function
derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
49. Процедура вычисления корня уравнения (комбинированный метод).
{ Комбинированный метод }
Procedure Combination(a, b, eps : real; var x : real);
var
z : real;
begin
repeat
if fx(a)*derivat2(a, eps) > 0
then
begin
tangent(a, b, eps, z);
chord(b, a, x);
b := z; a := x
end
else
begin
tangent(b, a, eps, z);
chord(a, b, x);
b := x; a := z
end
until abs(z - x) < eps
end;
50. Процедура определения числа точек деления промежутка в зависимости от вычисляемой точности.
{ Процедура определения числа точек деления промежутка интегр. }
Procedure Number(a, b, eps : real; var
n : integer);
var
dy2, d, c, dx : real;
begin
c := (a + b)/2;
dy2 := derivat2(c, eps);
if dy2 = 0
then
begin
c := a; dx := (b - a)/10;
while derivat2(c, eps) = 0 do c := c + dx;
dy2 := derivat2(c, eps)
end;
n := 1;
d := abs((b - a)*(b - a)*(b - a));
while abs(dy2*d)/(24*n*n) >= eps do n := n+1;
end;
{--------------------------------------------------------------}
{ Вычисление интеграла методом прямоугольников }
Procedure Rectangle(a, b : real; n : integer; var j : real);
var
dx, c, f : real; i : integer;
begin
dx := (b - a)/n; c := a + dx/2;
f := fx(c);
for i := 1 to n - 1 do
begin
c := c + dx;
f := f + fx(c)
end;
j := dx * f
end;
51. Процедура вычисления интеграла по формуле прямоугольников.
{ Вычисление интеграла методом прямоугольников }
{ Rectangle - прямоугольник }
Procedure Rectangle(a, b : real; n : integer; var j : real);
var
dx, c, f : real;
i : integer;
begin
dx := (b - a)/n;
c := a + dx/2;
f := fx(c);
for i := 1 to n - 1 do
begin
c := c + dx;
f := f + fx(c)
end;
j := dx * f
end;
52. Процедура вычисления интеграла по формуле трапеций.
{ Вычисл. интеграла по формуле трапеций. Trapezoid - трапеция }
Procedure Trapezoid(a, b : real; n : integer; var j : real);
var
dx, c, f : real;
i : integer;
begin
dx := (b - a)/n; c := a;
f := (fx(a)) + fx(b))/2;
for i := 1 to n - 1 do
begin
c := c + dx;
f := f + fx(c)
end;
j := dx * f
end;
53. Процедура вычисления интеграла по формуле Симпсона.
Procedure Simpson(a, b : real; n : integer; var j : real);
var
dx, c, c1, f : real;
i : integer;
begin
dx := (b - a)/n;
c := a;
c1 := a + dx/2;
f := fx(a) + fx(b) + 4*fx(c1);
for i := 1 to n - 1 do
begin
c := c + dx; c1 := c1 + dx;
f := f + 2*fx(c) + 4*fx(c1)
end;
j := (dx/6)* f
end;
54. Процедуры вычисления интеграла по методу Монте-Карло.
Function I(n : longint; a, b : real) : real;
var
x, f : real; k : longint;
begin
randomize;
f := 0;
for k := 1 to n do
begin
x := random*(b - a) + a;
f := f + fx(x)
end;
I := (b - a)*f/n
end;
{----------------------------------------------------------------------------------------}
Procedure Monte_Karlo(a, b, eps : real; var s : real);
var
t, d, f, dd : real; n : longint;
begin
n := 1;
t := I(n, a, b);
s := t;
d :=0;
repeat
n := n + 1;
t := t + I(n, a, b);
s := t/n;
d := d + (n/(n - 1))*sqr(I(n, a, b) - s);
dd := d/(n - 1)
until 5*sqrt(dd/n) < eps
end;
Упражнения
184. Вычислить значение дифференциала функции

185.

186. Доказать, что функция y = ex sinx удовлетворяет соотношению


187. Решите уравнения, выбирая подходящий метод решения:
x3 - 9x + 2 = 0, xeч = 2, x = 0.538sinx + 1, aч = ax при a > 1, x2 arctgx = a, где

188. Решить уравнение


189. Пользуясь правилами прямоугольника, трапеции и правилом Симпсона, вычислить приближенно число



190. Вычислить

Найти модуль перехода от натурального логарифма к десятичному.
191. Вычислить по формуле Симпсона или методом Монте-Карло.





192. В следующих задачах при нахождении пределов интегрирования необходимо воспользоваться методами приближенного решения уравнений.
а) Найти площадь фигуры, ограниченной дугами парабол y = x3- 7 и
y = - 2x2+ 3x и осью ординат.
б) Найти площадь фигуры, ограниченной параболой y = x3 и прямой
y = 7(x + 1).
в) Найти площадь фигуры, ограниченной параболой y=16 - x3 и полукубической параболой y =

193. Вычислить двойной интеграл по методу Монте-Карло:

если область (A) ограничена двумя параболами: y = x2 и y2 = x.
Ответы
К
заданию 1
Program derivative2;
uses WinCrt;
var
x0, eps, dx, dy, dy3 : real;
Function fx(x : real) : real;
begin
fx := x*x*x*x
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления второй производной }
Function derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите точку, в которой находится ');
write('вторая производная '); readln(x0);
write(' Введите точность вычисления второй производной ');
readln(eps);
dy := derivat2(x0, eps);
write('Вторая производная функции в точке ', x0:6:t(eps));
writeln(' равна ', dy:6:t(eps));
writeln('с точностью до ', eps:1:t(eps))
end.
К заданию 3
{ Выбор метода решения уравнений: метод хорд, метод касательн. }
{ комбинированный метод }
Program Case_method;
uses WinCrt;
var
a, b, x, eps : real;
k : integer;
{----------------------------------------------------------------------------------------}
{ Заданная функция }
Function fx(x : real) : real;
begin
fx := x*sin(x) - 0.5
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Вычисление 1-й производной }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs((dy2*dy2*fx(x0))/(2*dx)) < eps;
derivat1 := dy/dx
end;
{----------------------------------------------------------------------------------------}
{ Вычисление 2-й производной }
Function derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
{----------------------------------------------------------------------------------------}
{ Процедура определения наименьшего значения производной }
{ на заданном промежутке }
Procedure minimum(a, b, eps : real; var min : real);
var
d : real;
begin
a := a - eps;
b := b + eps;
repeat
a := a + eps;
b := b - eps;
min := abs(derivat1(a, eps));
d := abs(derivat1(b, eps));
if min > d then min := d
until min <> 0
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом хорд }
Procedure chord1(a, b, eps : real; var
x : real);
var
x1, min : real;
begin
minimum(a, b, eps, min);
x1 := a;
repeat
x := x1 - ((b - x1)*fx(x1))/(fx(b) - fx(x1));
x1 := x
until abs(fx(x))/min < eps
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом касательных }
Procedure tangent1(a, b, eps, min : real; var x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - fx(x1)/derivat1(x1, eps);
x1 := x
until abs(fx(x))/min < eps
end;
{----------------------------------------------------------------------------------------}
Procedure Tangent2(a, b, eps : real; var x : real);
var
min : real;
begin
minimum(a, b, eps, min);
if fx(a)*derivat2(a, eps) > 0
then tangent1(a, b, eps, min, x)
else tangent1(b, a, eps, min, x)
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом хорд }
Procedure chord(a, b : real; var
x : real);
begin
x := a - ((b - a)*fx(a))/(fx(b) - fx(a))
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом касательных }
Procedure tangent(a, b, eps : real; var
z : real);
begin
z := a - fx(a)/derivat1(a, eps)
end;
{----------------------------------------------------------------------------------------}
{ Комбинированный метод }
Procedure Combination(a, b, eps : real; var x : real);
var
z : real;
begin
repeat
if fx(a)*derivat2(a, eps) > 0
then
begin
tangent(a, b, eps, z);
chord(b, a, x);
b := z; a := x
end
else
begin
tangent(b, a, eps, z);
chord(a, b, x);
b := x; a := z
end
until abs(z - x) < eps
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите левый конец промежутка a = '); readln(a);
write('Введите правый конец промежутка b = '); readln(b);
write('Введите точность вычисления корня eps = ');
readln(eps);
writeln('Для выбора метода решения, введите его номер ');
writeln('1 - метод хорд, 2 - метод касательных');
writeln(' 3 - комбинированный метод'); readln(k);
Case k of
1 : chord1(a, b, eps, x);
2 : Tangent2(a, b, eps, x);
3 : Combination(a, b, eps, x)
end;
writeln('Корень уравнения равен x = ', x:6:t(eps));
writeln('С точностью до eps = ', eps:1:t(eps))
end.
К заданию 4
{ Вычисление интеграла по формуле трапеций }
Program integral_trapezoid;
uses WinCrt;
var
a, b, eps, j : real;
n : integer;
Function fx(x : real) : real;
begin
fx := 1/x
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления второй производной }
Function derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
{----------------------------------------------------------------------------------------}
{ Процедура определения числа точек деления промежутка интегр. }
Procedure Number(a, b, eps : real; var
n : integer);
var
dy2, d, c, dx : real;
begin
c := (a + b)/2;
dy2 := derivat2(c, eps);
dx := (b - a)/10;
if dy2 = 0
then
begin
c := a;
while derivat2(c, eps) = 0 do c := c + dx;
dy2 := derivat2(c, eps)
end;
n := 1;
d := abs((b - a)*(b - a)*(b - a));
while abs(dy2*d)/(12*n*n) >= eps do n := n+1;
end;
{----------------------------------------------------------------------------------------}
{ Вычисл. интеграла по формуле трапеций. Trapezoid - трапеция }
Procedure Trapezoid(a, b : real; n : integer; var j : real);
var
dx, c, f : real;
i : integer;
begin
dx := (b - a)/n;
c := a;
f := (fx(a) + fx(b))/2;
for i := 1 to n - 1 do
begin
c := c + dx;
f := f + fx(c)
end;
j := dx * f
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите нижний предел интегрирования '); readln(a);
write('Введите верхний предел интегрирования '); readln(b);
write('Введите точность вычисления интеграла ');
readln(eps);
Number(a, b, eps, n);
Trapezoid(a, b, n, j);
writeln('Значение интеграла равно ', j:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
2-й способ
{ Вычисление интеграла по формуле трапеций }
Program integral_trapezoid;
uses WinCrt;
var
a, b, eps, max, j : real;
n : integer;
Function fx(x : real) : real;
begin
fx := 1/x
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления второй производной }
Function derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
{----------------------------------------------------------------------------------------}
{ Определение наибольшего значения второй производной }
Procedure Maximum(a, b, eps : real; var
max : real);
var
dx, x : real;
begin
dx := 0.1; x := a;
max := abs(derivat2(x, eps));
while x<= b do
begin
x := x + dx;
if max < abs(derivat2(x, eps))
then max := abs(derivat2(x, eps))
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура определения числа точек деления промежутка интегр. }
Procedure Number(a, b, eps, max : real; var
n : integer);
var
d : real;
begin
n := 1;
d := abs((b - a)*(b - a)*(b - a));
while (max*d)/(24*n*n) >= eps do n := n+1;
end;
{----------------------------------------------------------------------------------------}
{ Вычисл. интеграла по формуле трапеций. Trapezoid - трапеция }
Procedure Trapezoid(a, b : real; n : integer; var j : real);
var
dx, c, f : real;
i : integer;
begin
dx := (b - a)/n;
c := a;
f := (fx(a) + fx(b))/2;
for i := 1 to n - 1 do
begin
c := c + dx;
f := f + fx(c)
end;
j := dx * f
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите нижний предел интегрирования '); readln(a);
write('Введите верхний предел интегрирования '); readln(b);
write('Введите точность вычисления интеграла '); readln(eps);
Maximum(a, b, eps, max); Number(a, b, eps, max, n);
Trapezoid(a, b, n, j);
writeln('Значение интеграла равно ', j:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
К заданию 6
{ Вычисление интеграла методом Монте-Карло }
Program integral_Monte_Karlo;
uses WinCrt;
var
a, b, eps : real;
n : longint;
{----------------------------------------------------------------------------------------}
Function fx(x : real) : real; { Промежуток интегрир. [3, 4] }
begin { Интеграл хорошо вычисл. с точн. до 0.00001 }
fx := sin(0.2*x - 3)/(x*x + 1)
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол- во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления интеграла методом Монте-Карло }
Function I(n : longint; a, b : real) : real;
var
x, f : real;
k : longint;
begin
randomize;
f := 0;
for k := 1 to n do
begin
x := random*(b - a) + a;
f := f + fx(x)
end;
I := (b - a)*f/n
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите нижний предел интегрирования '); readln(a);
write('Введите верхний предел интегрирования '); readln(b);
write('Введите точность вычисления '); readln(eps);
n := 10;
repeat
n := 2*n
until abs(I(n, a, b) - I(2*n, a, b)) <= eps;
writeln('Значение интеграла равно ', I(2*n, a, b):6:t(eps));
writeln('С точностью до ', eps:1:t(eps));
end.
Приближенное вычисление интегралов с помощью рядов
С помощью почленного интегрирования рядов получаются разложения в бесконечные степенные ряды для некоторых интегралов, не выражающихся в конечном виде через элементарные функции. Эти разложения могут быть использованы для приближенных вычислений.
Так, исходя из разложения

найдем значение интеграла

Вначале разложим в ряд функцию


Интегрируем почленно этот ряд, получим:

который сходится на множестве всех действительных чисел.
Чтобы составить программу, найдем рекуррентную формулу для вычисления суммы ряда.



отсюда получаем:

Так как ряд знакочередующийся, то оценить точность вычисления можно по абсолютной величине последнего "отброшенного" члена, т. е. по значению

Программа
Program Problem1;
uses WinCrt;
var
n : longint;
u, I, x, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите значение аргумента x '); readln(x);
write('Введите точность вычисления '); readln(eps);
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -(u*x*x*(2*n - 1))/(2*n*(2*n + 1))
until abs(u) < eps;
writeln('Значение интеграла равно ', I:6:t(eps))
end.
В теории вероятностей нам придется иметь дело с функцией - интегралом вероятностей

Надо лишь заметить, что значение этой функции при


Для составления программы вычисления значений этого интеграла и большего удобства использования в других программах, создадим функцию:
{ Рекуррентная функция вычисления интеграла вероятностей }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
Использование ее в программе приводится ниже.
Program Problem2;
uses WinCrt;
var
x, eps : real;
{----------------------------------------------------------------------------------------}
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
Function FF(x, eps : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < eps;
FF := 2*I/sqrt(2*Pi)
end
end;
{-----------------------------------------------------------------------------------------}
begin
write('Введите значение аргумента x '); readln(x);
write('Введите точность вычисления '); readln(eps);
writeln('Значение интеграла вероятностей равно ', FF(x, eps):6:t(eps))
end.
Аналогично предыдущему примеру вычислим интеграл

Для этого надо вспомнить ряд, в который разлагается функция sinx

при всех

Разложим в ряд


Интегрируя его, получим:

Найдем рекуррентную формулу для составления программы.



Оценить точность можно по абсолютной величине n-го члена, т. е. по величине

Составим процедуру вычисления этого интеграла.
Procedure
Integral(x, eps : real; var I : real);
var
n : integer;
u : real;
begin
u := x; n := 1; I := 0;
repeat
I := I + u;
n := n + 1;
u := -(u*x*x*(2*n - 3))/((2*n - 2)*sqr(2*n - 1))
until abs(u) < eps
end;
Программа
Program Problem2;
uses WinCrt;
var
I, x, eps : real;
{----------------------------------------------------------------------------------------}
Procedure
Integral(x, eps : real; var I : real);
var
n : integer;
u : real;
begin
u := x; n := 1; I := 0;
repeat
I := I + u;
n := n + 1;
u := -(u*x*x*(2*n - 3))/((2*n - 2)*sqr(2*n - 1))
until abs(u) < eps
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите значение аргумента x '); readln(x);
write('Введите точность вычисления '); readln(eps);
Integral(x, eps, I);
writeln('Значение интеграла равно ', I:6:t(eps))
end.
Задание 6
Вычислить с помощью разложения в ряд интеграл

5.1. Полный эллиптический интеграл 2-го рода
Полный эллиптический интеграл 1-го рода

Полный эллиптический интеграл 2-го рода

Поставим задачу разложить эти интегралы по степеням модуля k (0 < k < 1). Для этого, положим в формуле интеграла 1-го рода



Этот ряд сходится равномерно относительно



следовательно, допустимо почленное интегрирование, получим:

Аналогично, исходя из формулы

найдем

Ряды (1) и (2) являются частными случаями биномиального ряда при


Найдем рекуррентную формулу для вычисления суммы



Процедура
Procedure Elliptic2(k, eps : real; var
Ek : real);
var
n : integer;
u : real;
begin
u := k*k/4; n := 1; Ek := 0;
repeat
Ek := Ek + u;
n := n + 1;
u := (u*k*k*(2*n - 1)*(2*n - 3))/(4*n*n);
until abs(u) < eps;
Ek := Pi*(1 - Ek)/2
end;
Программа
Program Problem3;
uses WinCrt;
var
Ek, k, eps : real;
{----------------------------------------------------------------------------------------}
Procedure
Elliptic2(k, eps : real; var Ek : real);
var
n : integer;
u : real;
begin
u := k*k/4; n := 1; Ek := 0;
repeat
Ek := Ek + u;
n := n + 1;
u := (u*k*k*(2*n - 1)*(2*n - 3))/(4*n*n);
until abs(u) < eps;
Ek := Pi*(1 - Ek)/2
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите значение аргумента 0 < k < 1 '); readln(k);
write('Введите точность вычисления '); readln(eps);
Elliptic2(k, eps, Ek);
writeln('Значение интеграла равно ', Ek:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
Задание 7
Составить программу вычисления эллиптического интеграла 1-го рода и сравнить результат с результатом, полученным с помощью бесконечных произведений.
Применение метода Монте-Карло для вычисления площадей фигур
Рассмотрим применение метода Монте-Карло для определения площадей фигур, ограниченных линиями.
Пример 7. Вычислить площадь фигуры, ограниченной линиями

Решение
Прежде необходимо установить ту фигуру, площадь которой требуется найти. Эта фигура заключена между осью OX, - уравнение y = 0; параболой с вершиной в точке (0; 0) и двумя прямыми, параллельными оси OY и проходящими через точки 1 и 2 на оси OX.
Установим, внутри какой простой фигуры (квадрата, прямоугольника и т.п.) может быть заключена заданная сложная фигура (см. рис. 39).
Рис. 39
По рисунку легко установить, что такой фигурой является прямоугольник с вершинами в точках (1; 0), (2; 0), (2; 4) и (1; 4). Площадь этого прямоугольника равна: Sпр = 4.
Значит площадь искомой фигуры будет равна:

Дальнейший ход решения такой же, как и в предыдущем примере.
"Бросаются" точки в прямоугольник. Их случайные координаты задаются так: x := random + 1, y := random*4.
Какие точки попадут в фигуру, площадь которой надо найти? Координаты точек, попадающих в фигуру, должны удовлетворять неравенствам:




На основе этих соображений составляем программу
Program Problem7;
uses WinCrt;
var
x, y, s, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random + 1; y := random*4;
if y < x*x then m := m + 1
end;
s := 4*m/n;
writeln('Площадь фигуры равна ', s:1:6);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Пример 8. Вычислить площадь фигуры, ограниченной линиями


Начертим заданную фигуру. Графиком функции y = 3 - 2x - x2 является парабола, ветви которой направлены вниз, а вершина находится в точке (-1; 4). В самом деле, выделим квадрат двучлена, получим:
y = -(x2 + 2x + 1 - 1 - 3) = -(x + 1)2 + 4.
Графиком функции y = 1 - x является прямая, проходящая через точки (1; 0) и (0; 1).
Необходимо найти точки пересечения этих графиков. Для этого надо решить систему из уравнений, описывающих заданные функции:

Решая находим, 1 - x =3 - 2x - x2, отсюда получаем: x1 = -2, x2 = 1. Значит координаты точек пересечения будут: (-2; 3) и (1; 0).
Полученную фигуру можно заключить в прямоугольник с вершинами (-2; 0), (-2; 4), (1; 4) и (1; 0) (см. рис. 40).
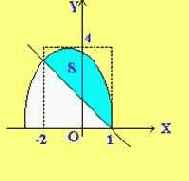
Рис. 40
Площадь этого прямоугольника равна


Чтобы "бросить" точку в этот прямоугольник, надо указать следующие случайные координаты этих точек: x := random*3 - 2 и y := random*4.
Точки, попавшие в заданную фигуру должны лежать "выше" прямой



Программа
Program Problem8;
uses WinCrt;
var
x, y, s, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random*3 - 2; y := random*4;
if (y <= 3 - 2*x - x*x) and
(y >= 1 - x) then m := m + 1
end;
s := 12*m/n;
writeln('Площадь фигуры равна ', s:1:6);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Задание 20
Вычислить площади фигур, ограниченных линиями:
1) y = 0, x = 0, x = 2, y = 1/(x + 1)2 +1;
2) y = cosx, y = 0, x = 0, x =

Библиотека часто встречающихся процедур и функций
31. Процедура вычисления вероятности биномиального закона распределения.
{ Рекуррентная процедура вычисления вероятности }
{биномиального закона распределения }
Procedure Recurro_binomial(n, m : integer; p : real; var pp : real);
var
i : integer;
begin
Extent(1 - p, n, pp);
for
i := 1 to m do pp := (pp*(n - i + 1)*p)/(i*(1 - p))
end;
32. Функция вычисления вероятностей по формуле Пуассона.
{ Функция вычисления вероятности распределения Пуассона }
Function PS(m : integer; a : real) : real;
var
i : integer;
pp : real;
begin
pp := exp(-a);
if m = 0 then pp := exp(-a)
else for i := 1 to m do pp := pp*a/i;
PS := pp
end;
33. Функция вычисления значений функции Гаусса:
{ Функция Гаусса }
Function G(x : real) : real;
begin
G := exp(-sqr(x)/2)/sqrt(2*Pi)
end;
34. Процедура вычисления вероятности по локальной формуле Муавра-Лапласа.
{ Процедура нахожд. вероятн. по локальной форм. Муавра-Лапласа }
Procedure Local_Laplace(n, m : longint; p : real; var pp : real);
var
x : real;
begin
x := (m - n*p)/sqrt(n*p*(1 - p));
pp := G(x)/sqrt(n*p*(1 - p))
end;
35. Функция вычисления интегральной функции Муавра-Лаплапса.
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if
x >= 5
then FF := 1
else if x <= -5
then
FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
36. Процедура вычисления вероятности появления события из заданного интервала [m1; m2].
{ Процедура вычисл. вероятн. наст. событ. из промеж. [m1; m2] }
Procedure Interval(n, m1, m2 : longint; p : real; var PP : real);
var
x1, x2 : real;
begin
x1 := (m1 - n*p)/sqrt(n*p*(1 - p));
x2 := (m2 - n*p)/sqrt(n*p*(1 - p));
PP := (FF(x2) - FF(x1))/2
end;
37. Процедура вычисления вероятности отклонения частоты m от заданного произведения np.
{ Процедура вычисления вероятности частоты наступления событий }
{ при заданной точности e - отклонении частоты от np }
Procedure
Probability(n : longint; p, e : real; var PP : real);
var
x : real;
begin
x := e/sqrt(n*p*(1 - p));
PP := FF(x)
end;
38. Процедура вычисления вероятности отклонения частости от вероятности в одном испытании (по абсолютной величине).
Procedure
ProbabilityLap(n : longint; p, e : real; var PP : real);
var
x : real;
begin
x := e*sqrt(n/(p*(1 - p)));
PP := FF(x)
end;
39. Процедура вычисления числа испытаний при заданной гарантированной вероятности и заданной точности частости.
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until
FF(x) >= PP
end;
Второй способ
нахождения значения n. Он основывается на следующей процедуре:
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure Number2(e, PP : real; var n : longint);
var
x : real;
begin
x := 0;
repeat
x := x + 0.0001
until
FF(x) >= PP;
n := trunc(sqr(x/(2*e)))
end;
40. Процедура нахождения аргумента функции Муавра-Лапласа
Procedure
Argument(PP : real; var x : real);
begin
x := 0;
repeat
x := x + 0.0001
until FF(x) >= PP
end;
Второй способ
{ Процедура нахождения аргумента функции Муавра-Лапласа }
Procedure
Argument(PP, eps : real; var x : real);
begin
x := 0;
repeat
x := x + eps
until FF(x) >= PP
end;
Упражнения
144. Вероятность солнечной погоды в некоторой местности для каждого дня равна 0,4. Какова вероятность того, что в течение трех дней хотя бы один день будет солнечным?
145. Минное заграждение поставлено в одну линию с интервалами между минами в 100 м. Какова вероятность того, что корабль шириной 20 м, пересекая это заграждение под прямым углом, подорвется на мине? (Размерами мины можно пренебречь.)
146. На окружности радиуса R наудачу выбирается точка. Найти вероятность того, что выбранная точка будет находиться от точки A, фиксированной на данной окружности, на расстоянии, не превышающем R.
147. Из фиксированной вершины квадрата произвольным радиусом, меньшим его диагонали, проведена окружность. Какова вероятность того, что дуга пересечет стороны квадрата, имеющие эту вершину одним из своих концов?
148. В круг радиуса R вписан правильный шестиугольник. Какова вероятность того, что наудачу выбранная точка внутри круга окажется внутри шестиугольника?
149. Шар радиуса r = 2 см наудачу бросают в круг радиуса R=25 см, в котором вырезано квадратное отверстие со стороной a = 14 см. Какова вероятность того, что шар пройдет через это отверстие, не задев его края, если он непременно попадет в круг?
150. В 25 см от центра шара, радиус которого равен 15 см, находится точечный источник света. Какова вероятность того, что наудачу взятая точка на поверхности шара окажется освещенной?
151. На отрезке AB длины a наудачу выбирается точка M, а на отрезке CD длины b
- точка N. Какова вероятность того, что точки M и N делят отрезки AB и CD так, что отношение


152. Точка A наудачу выбирается на окружности, радиус которой равен R, а точка B - на отрезке CD длины a. Найти вероятность того, что точка A окажется на дуге, длина которой равна R, а точка B окажется расположенной от конца C отрезка CD не далее чем на 0,4а.
153. Какова вероятность того, что две наудачу выбранные точки внутри круга радиуса R окажутся внутри вписанного в этот круг квадрата, если они выбираются независимо друг от друга?
154. Два действительных числа x и y выбираются наугад независимо друг от друга так, что сумма их квадратов меньше 64. Какова вероятность того, что сумма положительных x и y окажется меньше восьми?
Применение ряда Фибоначчи
Пример 2. Определение минимума функции с помощью ряда Фибоначчи.
Ряд Фибоначчи много интересных применений в математике. О некоторых из них мы поговорим позже, а на этом занятии разберем использование этого ряда для поиска минимума функции на заданном промежутке (смотри также В.Ф. Очков, Ю.В. Пухначев, "128 советов начинающему программисту", Москва, 1991 г.).
Для примера рассмотрим функцию

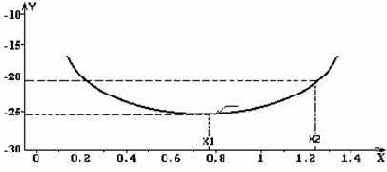
Рис. 23
Итак, стоит задача найти минимум функции на этом промежутке, т.е. значение x, при котором получается минимум и значение функции y в этой точке. Первая мысль, которая возникает - это делить отрезок (0, 2) пополам, затем выяснять, на каком из получившихся частей может находится минимум и делить эту часть пополам и так далее. Такой процесс возможен, но имеет два существенных недостатка.
Во-первых, "приближение" к точке минимума будет очень медленным, придется испробовать много вариантов, чтобы "подобраться" к искомой точке.
Во-вторых, при даже очень большом количестве делений точность приближения будет невелика.
Поэтому, возникает необходимость как-то иначе делить отрезок (если мы избрали метод деления отрезка). Но как? Отделять от одного конца 4-ю или 3-ю части и постепенно сужать отрезок к лучшему результату не приведет, пожалуй еще и к худшему.
Улучшить процесс деления отрезка помогает ряд Фибоначчи. Может даже возникнуть впечатление, что он как будто специально создан для этой цели. Хотя ряд возник совершенно из других более естественных соображений, он показывает число появления кроликов во 2-й, 3-й, 4-й и т. д. годы, если первоначально есть только одна самка и один самец. Но многие закономерности природы прекрасно описываются математическими средствами, вот и в нашем примере ряд Фибоначчи дает очень хорошие результаты.
Для деления отрезка можно задать число делений - n, а затем в зависимости от n определить коэффициент деления, как отношение (n - 1)-го и n-го членов ряда.
Если a - левый конец промежутка, b - правый, тогда разделить отрезок можно так: x2 := a + (b - a)*fib(n - 1)/fib(n); y2 := f(x2);
Для n = 10 отношение fib(9)/fib(10) = 34/55 = 0.6181818... . Тогда, правая граница станет равна: x2 := 1.236364... . Для дальнейшего процесса поиска, надо "приблизить" левый конец промежутка на такое же расстояние к правому концу (

В дальнейшем могут возникнуть несколько случаев.
Если x2 > x1 и y2 > y1, тогда в качестве правого конца промежутка принять x2 и зафиксировать его (b := x2), а x2 заменить на x1 (x2 := x1), y2 присвоить значение y1 (y2:=y1) и повторить процесс приближения левого конца к правому:
x1 := a + b - x2.
Если x2 <= x1 и y2 > y1, тогда a := x2; x2 := x1; y2 := y1 и повторить:
x1 := a + b - x2.
Если x2 > x1 и y2 < y1, тогда a := x1 и выполнить: x1 := a + b - x2.
Если x2 <= x1 и y2 <= y1, тогда b := x1 и выполнить: x1 := a + b - x2.
Если ни одно из этих условий не выполняется, тогда выполнятся оператор:
x1 := a + b - x2
и весь процесс повторяется.
Для составления программы потребуется функция, вычисляющая члены ряда Фибоначчи, уже знакомая нам:
{ Функция вычисления членов ряда Фибоначчи }
Function fib(n : integer) : real;
var
f, f1, f2 : real;
i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1; f1 := f;
f := f1 + f2
end;
fib := f
end;
Нужно будет вычислять значения заданной функции и для этого составим следующую функцию:
{ Заданная исследуемая функция }
Function
func(x : real) : real;
begin
func := x*x*x*x - 14*x*x*x + 60*x*x - 70*x
end;
Полностью программа
приводится ниже:
Program Minimumfib;
uses WinCrt;
label 1;
var
a, aa, bb, x, b, x1, x2, y1, y2 : real; i, n : integer;
{----------------------------------------------------------------------------------------}
{ Заданная исследуемая функция }
Function func(x : real) : real;
begin
func := x*x*x*x - 14*x*x*x + 60*x*x - 70*x
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления членов ряда Фибоначчи }
Function fib(n : integer) : real;
var
f, f1, f2 : real; i: integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1;
f1 := f;
f := f1 + f2
end;
fib := f
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите нижнюю границу промежутка '); readln(a);
aa := a;
write('Введите правую границу промежутка '); readln(b);
bb := b;
write('Введите число приближений к минимуму '); readln(n);
x2 := a + (b - a)*fib(n-1)/fib(n); y2 := func(x2);
for i := 1 to n do
begin
x1 := a + b - x2; y1 := func(x1);
if (x2 > x1) and (y2 > y1)
then
begin
b := x2; x2 := x1; y2 := y1; goto 1
end;
if (x2 <= x1) and (y2 > y1)
then
begin
a := x2; x2 := x1; y2 := y1; goto 1
end;
if (x2 > x1) and (y2 < y1)
then
begin
a := x1; goto 1
end;
if (x2 <= x1) and (y2 <= y1)
then
begin
b := x1; goto 1
end;
1: end;
x := (a + b)/2;
write('Мин.
значение функции на (');
writeln(aa:1:0, ',', bb:2:0, ')');
writeln('Значение функции равно ', func(x):6:12);
writeln('При значении аргумента ', x:6:12)
end.
В этой программе число приближений устанавливается пользователем. Программу можно изменить, указав в условии цикла точность приближения значений аргумента x. Но тогда придется каждый раз при повторении цикла изменять коэффициент деления, так неизвестно конечное число повторений цикла. Для этого можно добавить в программу процедуру вычисления границ промежутка:
{ Процедура вычисления знач. аргумента и функции }
{ approach - приближение }
Procedure approach(a, b : real; n : integer; var x2, y2 : real);
begin
x2 := a + (b - a)*fib(n - 1)/fib(n);
y2 := func(x2)
end;
И тогда, программа станет следующей:
{Поиск минимума функции методом Фибоначчи}
Program Minimumfib;
uses WinCrt;
label 1;
var
a, aa, bb, x, b, x1, x2, y1, y2, e : real;
n : integer;
{----------------------------------------------------------------------------------------}
{ Заданная исследуемая функция }
Function func(x : real) : real;
begin
func := x*x*x*x - 14*x*x*x + 60*x*x - 70*x
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления членов ряда Фибоначчи }
Function fib(n : integer) : real;
var
f, f1, f2 : real;
i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1;
f1 := f;
f := f1+f2
end;
fib := f
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления знач.
аргумента и функции }
{ approach - приближение }
Procedure approach(a, b : real; n : integer;
var x2, y2 : real);
begin
x2 := a + (b - a)*fib(n-1)/fib(n);
y2 := func(x2)
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write(' Введите нижнюю границу промежутка '); readln(a);
aa := a;
write('Введите правую границу промежутка '); readln(b);
bb := b;
write('Введите точность приближения '); readln(e); n := 3;
approach(a, b, n, x2, y2);
while abs(b - a) > e do
begin
x1 := a + b - x2; y1 := func(x1);
if (x2 > x1) and (y2 > y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
b := x2; x2 := x1; y2 := y1; goto 1
end;
if (x2 <= x1) and (y2 > y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
a := x2; x2 := x1; y2 := y1; goto 1
end;
if (x2 > x1) and (y2 < y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
a := x1; goto 1
end;
if (x2 <= x1) and (y2 <= y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
b := x1; goto 1
end;
n := n + 1;
approach(a, b, n, x2, y2);
1: end;
x := (a + b)/2;
write('Мин. значение функции на промежутке (');
writeln(aa:1:0,',',bb:2:0,')');
writeln('Значение функции равно ', func(x):6:12);
writeln('При значении аргумента ', x:6:12)
end.
Очень часто, при поиске минимума функции для деления отрезка используют так называемое "Золотое сечение".
"Золотое сечение" или "золотое сечение" - деление отрезка на две части так, что большая из них есть средняя пропорциональная между меньшей частью и всем отрезком. Если a - весь отрезок, x - большая из двух частей, тогда:
a : x = x : (a - x)
Решая это уравнение, получаем:


Зная это, можно составить программу поиска минимума функции, используя "золотое сечение", тогда:
x1 := 0.618*a + 0.382*b, x2 := 0.382*a + 0.618*b.
Для вычисления этих значений можно составить две процедуры, которые затем использовать в программе.
Procedure gold1(a, b : real; var
x1, y1 : real);
begin
x1 := 0.618*a + 0.382*b; y1 := fx(x1)
end;
{------------------------------------------------------}
Procedure gold2(a, b : real; var
x2, y2 : real);
begin
x2 := 0.382*a + 0.618*b; y2 := fx(x2)
end;
Программирование в среде Microsoft Windows на языке Pascal
В этой части занятия описывается программирование с помощью компиляторов Turbo Pascal for Windows и Borland Pascal for Windows.
Ясно, что эта часть занятия будет полезна тем, кто работает в среде Windows.
На этом занятии мы не будем останавливаться на огромных возможностях, которые предоставляет интегрированная среда Borland Pascal, а узнаем начальные этапы работы. Прежде выясним, как можно программы, разработанные на Turbo Pascal 7 запустить в среде Borland Pascal.
Для этого, забегая несколько вперед, познакомимся с тем, что такое модули и каким модулем надо пользоваться, чтобы программа, написанная в DOS, могла работать в среде Windows.
Что такое модуль?
Модуль представляет собой набор констант, типов данных, переменных, процедур и функций. Каждый модуль по своей структуре аналогичен отдельной программе. Вместе с тем структура модуля позволяет использовать его как своеобразную библиотеку описаний.
В Borland Pascal входит 7 модулей. На этом занятии мы познакомимся с одним из них - WinCRT.
Модуль WinCRT может быть использован для преобразования DOS-программ и создания небольших Windows программ.
Для этого необходимо включить в начале DOS-программы следующую строку:
uses WinCrt;
Для примера рассмотрим приведенную выше программу Serg. В DOS она имела следующий вид:
Program Serg;
var
a, b, c: integer;
begin
write('Введите число лет, которое было бы Сереже '); readln(a);
b := a + 17;
c := b div 3;
writeln('Сереже было ', c, ' лет')
end.
Добавим в начала этой программы модуль WinCrt и программа сможет работать в среде Borland Pascal. В этом случае она станет такой:
Program Serg;
uses WinCrt;
var
a, b, c: integer;
begin
write('Введите число лет, которое было бы Сереже '); readln(a);
b := a + 17;
c := b div 3;
writeln('Сереже было ', c, ' лет')
end.
Теперь поговорим о среде разработчика. После запуска программы BPW (так в Windows записан Borland Pascal for Windows) на экране появляется следующее окно (см.
рис. 9):
Рис. 9
Чтобы набрать текст программы, достаточно выбрать из верхнего меню "File" и "щелкнуть" один раз левой кнопкой мыши. Окно разработчика примет вид (см. рис. 10):
Рис. 10
Из "выпавшего" меню следует выбрать "New" и нажать <Enter> или "щелкнуть" один раз левой кнопкой мыши. Окно очистится и предоставит пользователю возможность набирать текст программы на "чистом" поле (см. рис. 11).
Рис. 11
Перед началом ввода текста программы желательно установить шрифт, с котором вы будете работать. Желательно выбрать шрифт с кириллицей, т. е. такой, чтобы можно было бы набирать и русский текст.
Для установки шрифта следует выбрать в верхнем меню опцию "Options" и нажать <Enter> или "щелкнуть" один раз левой кнопкой мыши. "Выпадает" новое меню, из которого надо выбрать опцию "Environment" ("Среда") (см. рис. 12).
Рис. 12
После установки курсорной доски на слово "Environment" справа появляется новое меню, которое является своеобразным подменю раздела "Environment", которое состоит из следующих разделов:

Editor ...
Mouse ...
Startup ...
Highlight ...
Из появившегося меню надо выбрать "Editor ..." и нажать <Enter> или "щелкнуть" один раз левой кнопкой мыши. На экране появится меню, в котором из раздела "Font", "наступив" на указатель выбора шрифта можно выбрать нужный шрифт, название которого появится в видимом окне (см. рис. 13).
Рис. 13
После выбора шрифта можно набирать текст программы. Текст программы набран. Как выполнить пуск программы? Для этого из верхнего меню выбираем "Run" ("Пуск"), "выпадает" меню опции "Run" (см. рис. 14):
Рис. 14
Следует выбрать "Run Ctrl+F9". Программа будет запушена и выполнена.
Для записи программы на диск, следует выбрать опцию "File" из верхнего меню. Выбрать "Save" или "Save as" и записать в нужный каталог и под указанным именем свою программу (см. рис. 15).
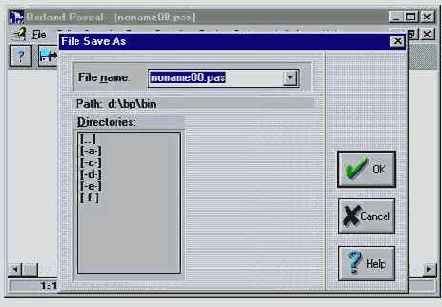
Рис. 15
Если программа была уже записана на диск и вам потребовалось ее вызвать для доработки или запуска в работу, тогда следую выбрать из меню опции "File" "Open" ("Открыть"), выбрать нужный каталог, файл и работать с программой (см. рис. 16).
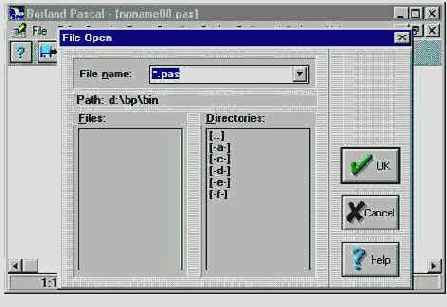
Рис. 16
В дальнейшем мы будем составлять и выполнять программы в интегрированной среде Borland Pascal. Но если кто-то работает на Turbo Pascal 6 или 7, тогда достаточно не писать в начале программы обращение к модулю uses WinCrt или заключить это обращение в фигурные скобки, т. е. сделать в виде комментария. Все остальное в программах остается без изменения. И лишь в главах, где рассматриваются модули и объектно-ориентированное программирование отдельно будет оговорено использование модулей в DOS и Windows.
Программы с совместным использованием циклов repeat и while do
Пример 3.
Если мы сложим все цифры какого-либо числа, затем - все цифры найденной суммы и будем повторять это много раз, мы наконец получим однозначное число (цифру), называемое цифровым корнем данного числа. Например, цифровой корень числа 561 равен 3 (5 + 6 + 1 = 12; 1 + 2 = 3).
Составьте программу для нахождения числового корня числа.
Соображения по составлению программы
Ясно, что в программе должен быть цикл, который определяет сумму цифр числа. В свою очередь, этот цикл должен также выполняться до тех пор, пока значение суммы цифр не станет равным одной цифре, т.е. станет меньше 10, но остается больше 0. Для этого надо организовать еще один цикл, который будет являться внешним
по отношению к циклу, подсчитывающему сумму цифр.
Одна тонкая особенность! Каждый раз после выполнения внутреннего цикла подсчета суммы цифр, значение этой суммы надо присваивать переменной, в которой содержится первоначальное число, т. е. заменять число на его сумму, проверять условие (не является ли сумма меньше десяти) и продолжать цикл уже с новым числом - суммой, если условие не выполняется. А ту переменную, в которой накапливалась сумма надо каждый раз не забывать обнулять.
Итак, если введенное число было присвоено переменной n, а сумма его цифр переменной s, то после подсчета суммы цифр, переменная должна получить значение s (n:= s), проверить условие (n < 10), если оно еще не выполняется, тогда обнулить переменную s (s:= 0) и продолжить цикл подсчета суммы цифр.
Внешний цикл по проверке значения суммы организуем с помощью операторов repeat ... until
n < 10, а внутренний по подсчету суммы цифр с помощью операторов while
... do.
Программа
Program
Problem3; { Цифровой корень числа }
uses WinCrt;
var
n, a, s : integer;
begin
write('Введите натуральное число '); readln(n);
a := n;
repeat
s := 0;
while n <> 0 do
begin
s := s + n mod 10; n := n div 10
end;
n := s
until n < 10;
writeln('Цифровой корень числа ', a, ' равен ', n)
end.
Распределение Пуассона
Распределение Пуассона часто встречается в задачах, связанных с потоком событий.
Под потоком событий будем понимать последовательность событий, наступающих одно за другим в случайные моменты времени.
Примерами могут быть: поток вызовов на телефонной станции, поток заявок в системе массового обслуживания, последовательность распада частиц некоторого количества радия и др.
Простейший поток событий характеризуется следующими свойствами:
а) вероятность наступления того или иного числа событий за любой промежуток времени зависит только от длительности этого промежутка (а не от начала отсчета);
б) указанная вероятность не зависит от того, какое число событий наступило до начала рассматриваемого промежутка времени (отсутствие последствия);
в) за малый промежуток времени вероятность наступления одного события приближенно пропорциональна длительности такого промежутка, а вероятностью наступления двух или более событий можно пренебречь.
В качестве случайной величины X мы рассмотрим число событий простейшего потока, наступающих за фиксированный промежуток времени t.
Значениями этой случайной величины могут быть любые целые числа
m = 0, 1, 2, 3, ...
Соответствующие вероятности обозначим через

pm(t) есть вероятность того, что за фиксированный промежуток m времени t наступит ровно m событий простейшего потока.
Пусть


В результате несложных математических рассуждений приходим, что в пределе при


Решая это уравнение при начальном условии p0(0) = 1, находим искомую вероятность отсутствия событий за промежуток времени t;

Нетрудно получить и общую формулу для расчета вероятностей



Эта формула и дает закон распределения случайной величины X - числа событий простейшего потока, наступающих за промежуток времени t.
Статистический смысл параметра



мы можем толковать его правую часть как относительную частоту наступления некоторого события простейшего потока за промежуток времени наблюдения


Обычно произведение


Этот закон распределения и называют законом распределения Пуассона или законом редких явлений.
Замечание. При малых значениях p и больших значениях n распределение Пуассона может быть применено в качестве приближенного значения для биномиального распределения.
Обозначим np = a, тогда p = a/n, q = 1 - p = 1 - a/n. Разложим вероятность




Первый член этого разложения дает как раз вероятность в распределении Пуассона, откуда и следует приближенная (асимптотическая) формула

второй член в скобках может служить для оценки относительной погрешности этой приближенной формулы:

Составим процедуру для вычисления вероятности по формуле Пуассона.
Для этого выведем рекуррентную формулу для вычисления вероятности:

отсюда получаем соотношение:

При m = 0, получим

Пользуясь этими двумя формулами легко составить функцию вычисления вероятностей по формуле Пуассона.
{ Функция вычисления вероятности распределения Пуассона }
Function PS(m : integer; a : real) : real;
var
i : integer;
pp : real;
begin
pp := exp(-a);
if m = 0 then pp := exp(-a)
else for i := 1 to m do pp := pp*a/i;
PS := pp
end;
Составим программы решения следующих задач, используя эту процедуру.
Пример 1. Вероятность изделию быть бракованным равна 0.05. Найти вероятность того, что среди 1000 изделий 40 бракованных.
{ Распределение Пуассона }
Program Problem1;
uses WinCrt;
var
n, m : longint;
p, a : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления вероятности распределения Пуассона }
Function PS(m : integer; a : real) : real;
var
i : integer;
pp : real;
begin
pp := exp(-a);
if m = 0 then pp := exp(-a)
else for i := 1 to m do pp := pp*a/i;
PS := pp
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите общее число изделий '); readln(n);
write('Введите вероятность изделия быть бракованным '); readln(p);
writeln('Введите число бракованных изделий, вероятность ');
write('появления которых Вы находите '); readln(m);
a := n*p;
writeln('Вероятность ', m, ' бракованных изделий в ');
writeln('партии из ',n, ' изделий равна ', PS(m, a):1:6)
end.
Пример 2. Вероятность сбить самолет одним выстрелом из винтовки в определенных условиях равна 0.003. Определить вероятность поражения самолета, если сделано по одному выстрелу из 300 винтовок.
{ Распределение Пуассона }
Program Problem2;
uses WinCrt;
var
n : longint;
p, a : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления вероятности распределения Пуассона }
Function PS(m : integer; a : real) : real;
var
i : integer;
pp : real;
begin
pp := exp(-a);
if m = 0 then pp := exp(-a)
else for i := 1 to m do pp := pp*a/i;
PS := pp
end;
{---------------------------------------------------------------------------------------}
begin
write('Введите общее число выстрелов '); readln(n);
write('Введите вероятность попадания при одном выстр. ');
readln(p);
a := n*p;
write('Вероятность поражения самолета при ');
writeln(n, ' выстрелах равна ', (1 - PS(0, a)):1:6)
end.
Пример 3.
Прибор состоит из 200 деталей, каждая из которых за время t может выйти из строя с вероятностью p = 0.01.
Найти вероятность того, что за время t выйдут из строя: а) 3 детали; б) не более трех деталей; в) не менее двух деталей; г) от двух до четырех деталей включительно.
{ Распределение Пуассона }
Program Problem3;
uses WinCrt;
var
n, m, i : longint;
p, a, Sum : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления вероятности распределения Пуассона }
Function PS(m : integer; a : real) : real;
var
i : integer;
pp : real;
begin
pp := exp(-a);
if m = 0 then pp := exp(-a)
else for i := 1 to m do pp := pp*a/i;
PS := pp
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите общее число деталей '); readln(n);
write('Введите вероятность выхода изделия из строя '); readln(p);
writeln('Введите число изделий, вероятность выхода из');
write('строя которых Вы находите '); readln(m); writeln;
a := n*p;
Sum := 0;
for i := 0 to 3 do Sum := Sum + PS(i, a);
writeln('Вероятность того, что за указанное время ');
write('выйдет из строя ',m, ' изделия равна ');
writeln(PS(m, a):1:6);
writeln('не более ',m, ' изделий ', Sum:1:6);
Sum := 0;
for i := 0 to 1 do Sum := Sum + PS(i, a);
Sum := 1 - Sum;
writeln('выйдет из строя не менее 2 деталей ', Sum:1:6);
Sum := 0;
for i := 2 to 4 do Sum := Sum + PS(i, a);
writeln('выйдет из строя от 2 до 4 деталей ', Sum:1:6)
end.
Пример 4. При контролируемом производственном процессе доля брака равна 0.02. При обнаружении в партии из 150 изделий более 5 бракованных изделий вся партия задерживается. Определить вероятность того, что партия будет принята.
{ Распределение Пуассона }
Program Problem4;
uses WinCrt;
var
n, m, i : longint;
p, a, PP : real;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления вероятности распределения Пуассона }
Function PS(m : integer; a : real) : real;
var
i : integer;
pp : real;
begin
pp := exp(-a);
if m = 0 then pp := exp(-a)
else for i := 1 to m do pp := pp*a/i;
PS := pp
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите общее число изделий '); readln(n);
write('Введите вероятность изделия быть бракованным ');
readln(p);
writeln('Введите число бракованных изделий, вероятность ');
write('появления которых Вы находите '); readln(m);
a := n*p;
PP := 0;
for i := 0 to m do PP := PP + PS(i, a);
writeln('Вероятность ', m, ' бракованных изделий в ');
writeln('партии из ',n, ' изделий равна ', PP:1:6)
end.
Равномерное распределение в интервале (a, b)
Говорят, что случайная величина X распределена равномерно в конечном интервале (a, b), если все ее возможные значения сосредоточены на этом интервале и если плотность распределения ее вероятностей на этом интервале и если плотность распределения ее вероятностей на этом интервале постоянна. Если эту постоянную обозначить буквой C, то плотность равномерного распределения задается формулой

Для случайной величины X, равномерно распределенной в интервале



Параметр C определяется из условия нормирования:

откуда

Подставляя полученное значение C в формулу (2), мы находим, что вероятность попадания значения величины X в интервал (x1, x2) равна отношению длины этого интервала к длине всего интервала


Заметим, что обычно употребляемое выражение "выберем точку X наудачу в интервале



Различия между циклом - while и циклом - repeat
1. Оператор, находящийся в цикле while, повторяется до тех пор, пока условие удовлетворено (т.е. истинно). Последовательность операторов, находящихся в цикле repeat, повторяется до тех пор, пока условие не удовлетворено (т. е. ложно).
Следовательно, в цикле while используется условие продолжения цикла, а в цикле repeat
- условие окончания цикла.
2. В цикле while
повторяется один оператор (несколько операторов надо объединять в составной оператор с помощью операторных скобок begin ... end), а в цикле repeat
можно повторять несколько операторов без операторных скобок.
3. В цикле while
сначала проверяется условие, а после этого в зависимости от значения условия выполняется
или не выполняется оператор или группа операторов после слова do.
В цикле repeat
последовательность операторов выполняется один раз, а после этого проверяется условие, т. е. эта последовательность всегда выполняется хотя бы один
раз, а в цикле while операторы, составляющие тело цикла могут вообще не выполняться ни одного раза.
Размещения
Прежде вспомним некоторые основные понятия из математики, в частности из теории множеств.
Во-первых, что такое множество вообще? Понятие множества является основополагающим в математике и неопределяемым.
Под множеством понимается некоторая совокупность объектов, объединенных по какому-то общему признаку.
Так, можно говорить о множестве стульев и столов в классе, множестве натуральных чисел, целых, рациональных и действительных (вещественных) чисел.
Объекты, входящие в множество, мы будем называть элементами.
Число 5 является элементом множества натуральных чисел. Стол является элементом множества столов в классе. Обычно множества обозначаются большими латинскими буквами
A, B, C, D, ..., X, Y, Z, а их элементы - малыми буквами a, b, c, d, ..., x, y, z.
О том факте, что a является элементом множества A говорят, что a принадлежит
множеству A.
Обычно элементы множества записываются в фигурных скобках

Пусть нам даны множества A, с уже указанными его элементами, и множество B = {a1, a2, a3, a4}.
Как вы заметили, каждый элемент множества B является и элементом множества A. В этом случае говорят, что B является подмножеством множества A.
Определение. Если каждый элемент множества B является в то же время элементом и множества A, то говорят, что B есть подмножество (часть) A.
Очень часто нам будет важно знать не только элементы множества, но и порядок их расположения в множестве.
Если учитывается порядок расположения элементов в множестве, тогда множества, имеющие одинаковые элементы, но имеющие их разное расположение, будут для нас различными.
Например: Z = {z1, z2, z3, z4 } и B = {z2, z1, z3, z4} будут считаться разными, так как у них различен порядок расположения элементов.
Множество, в котором задан порядок следования элементов, называются упорядоченным.
Рассмотрим некоторые простые примеры.
Пример 1. В классе 12 учебных предметов. В день проводится 5 разных уроков. Сколькими способами может быть составлено расписание занятий.
Для простоты рассуждений обозначим учебные предметы числами от 1 до 12:
1, 2, 3, 4, 5, ..., 10, 11, 12.
По условию задачи, нам необходимо из этих 12 чисел выбирать по 5 чисел. Причем эти наборы из пяти чисел могут отличаться не только числами, но и расположением чисел, например, один из наборов будет: {1, 2, 3, 4, 5}; набор, который получается при перестановке этих же чисел {2, 1, 3, 4, 5}, также будет удовлетворять условию задачи.
В самом деле, пусть первый набор будет состоять из следующих предметов: {алгебра, физика, химия, история, литература}; тогда набор, полученный при перестановке хотя бы двух предметов уже даст новое расписание: {физика, алгебра, химия, история, литература}.
Таким образом, наборы из 5 чисел могут отличаться не только самими числами, но и порядком их расположения.
Такие подмножества называются в комбинаторике размещениями.
Определение. Размещением из n
элементов по k называется всякое упорядоченное подмножество данного множества, содержащее k элементов.
О размещениях можно сказать несколько иначе, правда менее строго с математической точки зрения, но более понятно для нас.
Размещением из n
элементов по k называется всякое подмножество данного множества, состоящее из k элементов, которое может отличаться не только элементами, но и порядком их расположения.
Например, из множества M = {1, 2, 3, 4} можно образовать 12 различных размещений, из 4 по 2:
{1, 2} {1, 3} {1, 4} {2, 3} {2, 4} {3, 4}
{2, 1} {3, 1} {4, 1} {3, 2} {4, 2} {4, 3}
Число размещений, взятых из n элементов по k, мы будем обозначать символом



Значит,




Возвращаемся к примеру 1. В нем, как теперь уже стало ясно, надо найти число размещений
из 12 по 5.
По формуле находим:



Вычислить число размещений можно другим способом:



Итак,

Словами можно сказать, что число размещений из n элементов по k равно произведению k элементов

Например,


Таким образом, составив процедуру вычисления размещений по этому принципу, мы избегаем недопустимо больших чисел, которые могут образовываться при вычисление факториалов и упрощаем составление программ, а также имеем возможность в дальнейшем применять процедуру размещений в других программах.
Процедура
размещений из n элементов по k элементов.
Procedure placement(n, k : integer; var
r : longint);
var
i : integer;
begin
r := 1;
for i := 1 to k do r := r*(n - k + i)
end;
Программа
Program Problem1;
uses WinCrt;
var
n, k, r : longint;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа размещений из n по k }
Procedure placement(n, k : integer; var
r : longint);
var
i : integer;
begin
r := 1;
for i := 1 to k do r := r*(n - k + i)
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите число всех предметов '); readln(n);
write('Введите число уроков в день '); readln(k);
Placement(n, k, r);
writeln('Число вариантов расписания равно ', r)
end.
Пример 2. Сколько различных четырехзначных чисел можно написать при помощи цифр 0, 1, 2, ..., 9?
Рассуждения могут быть очень простыми. Нам надо выяснить сколькими способами можно выбрать по 4 цифры из 10, причем важен порядок расположения цифр, так как 1234 и 2134 дают разные числа. Значит необходимо определить число размещений из 10 элементов по 4,

Но из этого количества чисел мы должны исключить те, которые начинаются цифрой 0, например, 0123, 0213 и т.п. Эти числа уже не будут четырехзначными.
Сколько таких чисел? Да столько, сколько трехзначных чисел получится из 9 цифр (без нуля), т. е. равное числу размещений из 9 элементов по 3,

Окончательное количество четырехзначных чисел, которые можно составить из 10 цифр равно разности:

Программа
Program Problem2;
uses WinCrt;
var
n, k, a, a1 : longint;
{----------------------------------------------------------------------------------------}
Procedure placement(n, k : integer; var r : longint);
var
i : integer;
begin
r := 1;
for i := 1 to k do r := r*(n - k + i)
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите заданное ко-во цифр '); readln(n);
write('Введите ко-во цифр, из скольких составляется число '); readln(k);
placement(n, k , a);
placement(n - 1, k - 1, a1);
writeln('Число различных 4-х знач. чисел, которые можно');
writeln('написать при помощи цифр 0, 1, 2, .., 9 равно ', a - a1)
end.
Разные задачи
Пример 1. Составить программу определения всех делителей числа n.
Когда ставится такая задача, то очень часто учащиеся предлагают такой способ решения.
Надо испробовать все натуральные числа, начиная от 1 до n и, если какое-то из них будет являться делителем числа n, тогда выдавать его на экран. Например, для числа 36, берем для проверки числа 1, 2, 3, ..., 36 и выбираем из них делители 36. Делители будут следующими: 1, 2, 3, 4, 6, 9, 12, 18 и 36.
Такой способ возможен. Но, если вы внимательно посмотрите на делители числа 36, то обнаружите, что все они находятся в интервале от 1 до 18, т.е. до половины числа 36 и лишь последний делитель - это само число.
Да и простая логика рассуждений убеждает нас, что делители будут располагаться именно в этом интервале: от 1 до

Если допустить мысль, что есть делитель больше половины числа, тогда умножив его только лишь на 2, мы получим число большее заданного.
Итак, становится ясным, что все делители числа, кроме самого, находятся в промежутке от 1 до

Отсюда возникает такой план составления программы: организовать цикл от 1 до

число n делится на число из этого промежутка, тогда вывести этот делитель на экран; продолжить цикл; выдать на экран само число.
Программа
Program
Problem1; { Простой алгоритм. 1 - способ }
uses WinCrt;
var
n, d : integer;
begin
write('Введите целое число '); readln(n);
d := 1;
writeln('Делители числа ', n);
repeat
if n mod d = 0 then write(d, ' ');
d := d + 1
until d > n div 2;
write(n)
end.
Но и при решении этой задачи машине можно помочь и облегчить ее работу. Здесь на помощь снова приходит математика.
Оказывается, для того чтобы найти делители числа n, достаточно обнаружить делители не превышающие

Все остальные делители получаются в результате деления числа n на найденные делители.
Например, если n = 30, то достаточно найти делители 1, 2, 3, 5 (натуральный квадратный корень из 30 равен 5), а все прочие делители получаются делением на найденные:
30 div 1 = 30;
30 div 2 = 15;
30 div 3 = 10;
30 div 5 = 6.



d*d<n (что является тем же, что и

Почему надо сделать именно так. Это становится понятным на примере для числа 36.


d = 1, d


цикл продолжается;
находится остаток от деления 36 mod 1 = 0; выдается 1 и частное от деления 36 на 1, 36 div 1 =36;
d = 2, d


цикл продолжается;
36 mod 2 = 0;
выдается 2 и частное от деления 36 на 2, 36 div 2 = 18;
d = 3, d


цикл продолжается;
36 mod 3 = 0;
выдается 3 и частное от деления 36 на 3, 36 div 3 = 12;
d = 4, d


цикл продолжается;
36 mod 4 =0;
выдается 4 и 36 div 4 = 9;
d = 5, d


цикл продолжается;
36 mod 5 <>0, ничего не выдается на экран,
цикл продолжается;
d = 6, d


Проверяется d = 6 (d


Если бы цикл продолжался, пока d

Программа
Program
Problem1a; { Делители числа. 2 - способ }
uses WinCrt;
var
n, d : integer;
begin
write('Введите целое число '); readln(n);
writeln('Делители числа ', n);
d := 1;
while d*d < n do
begin
if n mod d=0 then write(d, ' ', n div d, ' ');
d := d + 1
end;
if d*d = n then write(d); writeln
end.
Рекурсия
Такой процесс, когда в процедуре происходит обращение к самой себе, называется рекурсией
(рекурсия - возврат). (Происходит от латинского recurreus - возвращающийся).
Теперь нам предстоит более подробно поговорить о рекурсиях.
Рекурсия - это такой способ организации подпрограммы, при котором в ходе выполнения она обращается сама к себе.
Приведем примеры, которые уже стали классическими, использования рекурсий в подпрограммах:
Пример 10. Вычисление факториала числа.
Ниже приведена программа вычисления факториала числа, в которой используется рекурсивная процедура fac:
Procedure fac(n : integer; var f : real);
begin
if (n = 0) or (n = 1) then f := 1
else
begin
fac(n - 1, f);
f := f*n
end
end;
Разберемся детально в работе этой процедуры. Для этого снова обратимся к математике.
Для вычисления факториала числа n, т.е. n! надо умножить последовательно n натуральных чисел от 1 до n:

Так, 4! будет равно:

Это прямой путь вычисления или итеративный.
Возможен и другой путь вычисления:

Именно на этом принципе основана работа приведенной процедуры.
Пусть введено в программу значение 4 для вычисления факториала 4! Как будет работать процедура?
После начала ее работы, будет выполнена проверка:
if (n = 0) or (n = 1) then
f := 1
Понятно, что 4 не равно 0 и не равно 1, значит будет выполняться оператор после else, т. е. fac(n - 1, f), а это означает, что снова будет вызвана также процедура, но значение n уменьшится на единицу и станет равным 3; затем снова будет выполнена проверка условия:
if
(n = 0) or (n = 1) then f := 1 и переход к вызову процедуры fac(n - 1, f).
Значение n
уменьшится на 1 и станет равным 2 и т.
д. до тех пор, пока n не станет равным 1, а значение f получит значение 1 ( надо заметить, что при всех предыдущих операциях значение f оставалось равным 0, а точнее говоря, неопределенным).
После этого, начнется обратный процесс, в котором будет выполняться команда: f := f*n. Он будет происходить так:
f := 1*4; f := 4*3; f := 12*2; f := 24*1.
Образно говоря, при первоначальном процессе, значения n от 4 до 1 "запоминаются" в стековую память "Паскаль-машины", а при следующем процессе, значения n "считываются" из стековой памяти “Паскаль-машины”
и умножаются на значения f.
Условно-схематически это можно изобразить так: значения n запоминаются в стек-память "Паскаль-машины":
|
4 |
|||
|
3 |
4 |
||
|
2 |
3 |
4 |
|
|
1 |
2 |
3 |
4 |
Обязательным элементом в описании всякого рекурсивного процесса является некоторое утверждение, определяющее условие завершения рекурсии; иногда его называют опорным условием рекурсии (или "якорем"). В нашем случае это условие:
if
(n = 0) or (n = 1) then f := 1.
В опорном условии может быть задано какое-то фиксированное значение, заведомо достигаемое в ходе рекурсивного вычисления и позволяющего организовать своевременную остановку процесса; применительно к вычислению факториала им будет равенство 1! = 1. Таким образом, любое рекурсивное определение всегда содержит два элемента: условие завершения и способ выражения одного шага решения посредством другого, более простого шага.
Для четкого понимания происходящих при этом процессов необходимо иметь в виду, что:
а) при каждом вызове процедуры создается новый экземпляр f;
б) все экземпляры f накапливаются во внутреннем стеке “Паскаль-машины” и
в) в любой момент обработке доступен только один, хронологически последний экземпляр переменной f, который
г) по завершению очередного рекурсивного вызова автоматически уничтожается).
Вывод
При каждом входе в рекурсивную подпрограмму ее локальные переменные размещаются в особым образом организованной области памяти, называемой программным стеком.
Программа
Program Problem10;
uses WinCrt;
var
n : integer;
f : real;
{---------------------------------------------------------------------------------------}
Procedure fac(n : integer; var f : real);
begin
if (n=0) or (n=1) then f := 1
else
begin
fac(n - 1, f);
f := f*n
end
end;
{---------------------------------------------------------------------------------------}
begin
write('Введите натуральное значение n '); readln(n);
fac(n, f);
writeln('Факториал числа ', n, ' равен ', f:12:0)
end.
Турбо-Паскаль 7 или 6 дает очень удобную возможность пошаговой трассировки программы и процедуру. Для этого достаточно последовательно нажимать клавишу F7 и вы сможете полностью убедиться в правильности наших соображений.
Рекурсивная форма организации подпрограммы обычно выглядит изящнее итерационной (последовательной) и дает более компактный текст программы, но при выполнении, как правило, медленнее и может вызвать переполнение стека.
Как избавиться от этой неприятности вы узнаете позже. Но стоит знать, что при зацикливании программы следует выйти из нее нажатием <Ctrl>+<Z>+<Enter> (<Ввод>) (для Турбо-Паскаля 7 или 6).
Еще примеры с использованием рекурсивных процедур.
Пример 11. Над цепью озер летела стая белых гусей. На каждом озере садилось половина гусей и еще полгуся, а остальные летели дальше. Все гуси сели на семи озерах. Сколько гусей было в стае?
Решение
Математически задача решается устно очень остроумным способом.
Пусть вместе со стаей белых гусей все время летит еще один, Серый гусь.
Если к некоторому озеру подлетит m белых гусей и Серый, то на этом озере садится

А теперь выполним, образно говоря, прямые рассуждения для решения задачи.
Обозначим через xk количество летящих белых гусей, когда впереди еще k озер. Тогда условие задачи записывается так:

Отсюда получаем для последовательности (xk) рекуррентное соотношение

Зная его, легко составить рекурсивную процедуру:
Procedure goose(x, k : integer);
begin
if k = 1 then writeln(x) else
goose(2*x + 1, k - 1)
end;
В процедуру вводятся всего две переменные: x - искомое число гусей; k - число озер. Процедура устроена с расчетом, что гуси уже пролетели все 7 озер, значит надо вводить значение для x - один (1), а для k - семь (7). В процедуре устроено, что число k уменьшается на 1 и тогда опорным условием ("якорем") завершения процедуры является условие равенства 1 значений k и после этого на экран надо выдать значение числа гусей:
if k = 1 then writeln(x)
Опорное условие может быть и другим, если первоначальным значением k будет 1, тогда при повторном обращении к процедуре значение k надо не уменьшать, а увеличивать на 1 (k + 1), опорным условием, в этом случае, будет k = 7.
Ниже приводится законченная программа решения этой задачи:
Program Problem11;
uses WinCrt;
var
k : integer;
{----------------------------------------------------------------------------------------}
Procedure goose(x, k : integer);
begin
if k = 1 then write(x) else
goose(2*x + 1, k - 1)
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите число озер '); readln(k);
write('В стае было ');
goose(1, k);
writeln(' гусей')
end.
Придерживаясь подобных соображений, решите следующую задачу.
Решение уравнений с одной переменной методом половинного деления
Здесь мы очень кратко рассмотрим один из простых методов решения нелинейных уравнений - метод половинного деления, так как другие методы будут рассмотрены позже, после изучения последовательностей, массивов и множеств.
Главная цель этого небольшого раздела - показать использование функций, создаваемых пользователем в программах.
Отделение корней
Первый этап численного решения уравнения f(x) = 0 состоит в отделении корней, т.е. в установлении "тесных" промежутков, содержащих только один корень.
При отделении корней на некотором промежутке [a, b], мы потребуем, чтобы функция f(x) была непрерывна на этом промежутке и будем считать, что все интересующие нас корни находятся на промежутке [a, b], в котором f(a)*f(b) < 0.
Будем вычислять значения функции f(x), начиная с точки x = a, двигаясь вправо с некоторым шагом h. Как только обнаружится пара соседних значений f(x), имеющих разные знаки, и функция f(x) монотонна на этом отрезке, тогда значения аргумента x (предыдущее и последующее) можно считать концами отрезка, содержащего корень. Результатом решения этой задачи будет вывод значений концов промежутка.
Очевидно, что надежность рассмотренного подхода к отделению корней зависит как от характера функции f(x), так и от выбранной величины шага h. Действительно, если при достаточно малом значении h на концах текущего отрезка




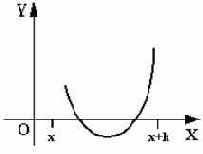
Рис. 24
Рис. 25
Предвидя подобные ситуации, следует выбирать при отделении корней достаточно малые значения h.
Давайте посмотрим как будет выглядеть программа отделения корней для функции

Ясно, что необходимо завести функцию, которая бы при необходимости обращения к ней вычисляла ее значения.
Эту функцию мы устроим уже известным нам способом и назовем fx:
Function fx(x : real) : real;
begin
fx := cos(x) - 0.1*x
end;
В основной программе, естественно потребовать от пользователя ввода границ промежутка и шага. В качестве границ промежутка будут переменные a и b, а для шага - h (в качестве значения шага, при выполнении программы возьмем 0.1).
Для подсчета числа промежутков будет служить счетчик k. Первоначальное значение левой границы: x1:=a; а первая правая граница будет равна сумме левой границы и шага: x2:=x1+h; значение функции в левой границе первого промежутка: y1:=fx(x1).
Последовательно к левой границе добавляется шаг h и так должно продолжаться пока
это значение не станет равно правой границе данного промежутка b. Значит, необходимо организовать цикл "пока": while x2 <= b do
В цикле, вычислять значение функции в точке x2, которая уже получилась от увеличения x1 на h: y2 := fx(x2).
Теперь следует проверить знак произведения значений функций на концах промежутка (fx(x1)*fx(x2)) и, если оно отрицательно, то на этом промежутке будет существовать корень, а значит надо выдать на экран координаты этого промежутка и его номер:
if y1*y2 < 0 then
begin
k := k + 1;
writeln(k,'-й корень на [',x1:6:4,'; ',x2:6:4,']')
end;
Далее следует продолжить движение к правой границе, а для этого выполнить следующие операторы:
x1 := x2; x2 := x1 + h; y1 := y2
Вот и вся несложная тактика этой программы. Полностью она приводится ниже:
Program
Separation_root; { Программа отделения корней }
uses WinCrt;
var
a, b, h, x1, x2, y1, y2 : real;
k : integer;
{----------------------------------------------------------------------------------------}
Function fx(x : real) : real;
begin
fx := cos(x) - 0.1*x
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите левую границу промежутка '); readln(a);
write('Введите правую границу промежутка '); readln(b);
write('Введите шаг '); readln(h);
k := 0;
x1 := a; x2 := x1 + h;
y1 := fx(x1);
while x2 <= b do
begin
y2 := fx(x2);
if y1*y2 < 0
then
begin
k := k+1;
writeln(k, '-й корень на [', x1:6:4, ';', x2:6:4, ']')
end;
x1 := x2; x2 := x1 + h;
y1 := y2
end
end.
Следующим, естественным этапом решения, является нахождение на промежутке корень с заданной степенью точности (если, конечно, уже известно, что он существует на нем).
Для этого нетрудно сочинить простую программу вычисления корня методом половинного деления, сущность которого заключается в следующем.
Известно, что на промежутке [a; b] есть корень. Зададим необходимую точность, с которой нам необходимо его вычислить. Обозначим ее - e.
Разделим промежуток [a; b] пополам. Точкой деления будет точка (см. рис. 25)

Рис. 25
Установим, на котором из полученных двух промежутков находится корень. Для чего найдем знак разности fx(a)*fx(c). Если этот знак отрицательный, тогда корень находится на левом промежутке. Заменив c на b (b:=c), мы получим новый промежуток, обозначенный прежними буквами (см. рис. 26):
Рис. 26
А если разность fx(a)*fx(c) не будет отрицательной, тогда корень находится на правом промежутке. Заменив c на a (a := c), мы получим новый промежуток для поиска корня, обозначенный теми же буквами (см. рис. 27):
Рис. 27
И такой процесс деления надо выполнять, пока разность между правой и левой границами по абсолютной величине будет больше заданной точности e
(

Пользуясь этими соображениями, нетрудно составить программу, где сам процесс половинного деления будет выполняться с помощью процедуры.
В качестве функции берется функция: f(x) := sin(2*x) - ln(x) и рассматривается на промежутке

После завершения основного цикла, находится окончательное значение x,


Program Division;
uses WinCrt;
var
a, b, c, e, x, d : real;
{----------------------------------------------------------------------------------------}
Function func(x : real) : real;
begin
func := sin(2*x) - ln(x)
end;
{----------------------------------------------------------------------------------------}
Procedure half(a, b, e : real; var x, d : real);
var
c : real;
begin
while abs(b - a) > e do
begin
c := (a + b)/2;
if func(a)*func(c) < 0 then b := c else a := c
end;
x := (a + b)/2;
d := abs(b - a)/2
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите левую границу промежутка '); readln(a);
write('Введите правую границу промежутка '); readln(b);
write('Введите точность вычисления корня '); readln(e);
half(a, b, e, x, d);
writeln('Значение корня равно x = ', x:6:10);
writeln('С границей погрешности ', d:2:10)
end.
Можно объединить программы отделения корня и уточнения его методом половинного деления в одну и получить программу, которая отделяет промежутки и сразу вычисляет на каждом из них корни с заданной точностью.
Программа
Program Equation;
uses WinCrt;
var
a, b, h, x1, x2, y1, y2, e, x, d : real;
k : integer;
{----------------------------------------------------------------------------------------}
Function fx(x : real) : real;
begin
fx := cos(x) - 0.1*x
end;
{----------------------------------------------------------------------------------------}
Procedure half(a, b, e : real; var x, d : real);
var
c : real;
begin
while abs(b - a) > e do
begin
c := (a + b)/2;
if fx(a)*fx(c) < 0 then b := c else
a := c
end;
x := (a + b)/2;
d := abs(b - a)/2
end;
{----------------------------------------------------------------------------------------}
begin
write(' Введите левую границу промежутка '); readln(a);
write('Введите правую границу промежутка '); readln(b);
write('Введите шаг '); readln(h);
write('Введите точность вычисления корня '); readln(e);
k := 0; x1 := a; x2 := x1 + h;
y1 := fx(x1);
while x2 <= b do
begin
y2 := fx(x2);
if y1*y2 < 0
then
begin
k := k + 1;
half(x1, x2, e, x, d);
write(k,'-й корень равен ', x:6:6);
writeln(' с погрешностью ', d:2:10)
end;
x1 := x2; x2 := x1 + h; y1 := y2
end
end.
Сходимость числовых и функциональных рядов
Пусть дан бесконечный ряд:

Станем последовательно складывать члены ряда, составляя (в бесконечном количестве) суммы;

их называют частными суммами (или отрезками) ряда.
Конечный или бесконечный предел




называется суммой ряда и пишут

Если ряд имеет конечную сумму, его называют сходящимся, в противном случае (т.е. если сумма равна


Попробуем установить являются ли некоторые ряды сходящимися?
Пример 3. Является ли ряд

Для установления этого, надо определить имеет ли предел последовательность частичных сумм ряда, а это в свою очередь, означает будет ли разность между суммами по абсолютной величине меньше заданного положительного, даже очень малого числа eps, т.е. будет ли выполняться неравенство:

Отсюда вытекает алгоритм составления программы.
Надо находить сумму членов ряда и как только разность между текущей суммой и следующей будет меньше eps, то цикл закончить, значит ряд сходится и выдать его сумму, которая будет равна текущей сумме с заданной степенью точности.
Установить является ли следующий ряд сходящимся и найти то число с заданной точностью eps, к которому он сходится.
Для вычисления суммы ряда нам придётся находить его члены и прибавлять к текущей сумме, а для нахождения членов ряда воспользуемся подпрограммой - функцией для вычисления факториала числа.
Программа
Program Problem3;
uses WinCrt;
var
n : integer;
z, z1, e, eps : real;
{----------------------------------------------------------------------------------------}
Function fakt(n : longint) : real;
var
i : longint;
f : real;
begin
f := 1;
if n = 0 then f := 1
else for i := 1 to n do
f := f*i;
fakt := f
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
begin
write(' Задайте точность eps '); readln(eps);
z := 0; n := 1;
repeat
z := z + sqr(fakt(n))/fakt(2*n);
n := n + 1;
z1 := z + sqr(fakt(n))/fakt(2*n)
until abs(z1 - z) < eps;
write('Сумма ряда равна ', z1:6:t(eps));
writeln(' с точностью до ', eps:3:t(eps))
end.
Задание 3
Установить, является ли ряд

Сочетания
Пусть M - конечное (не обязательно упорядоченное) множество, состоящее из n элементов.
Определение. Сочетанием из n элементов по k называется любое подмножество множества

Другими словами, в сочетаниях не важен порядок элементов, а важен лишь их состав. Так, например, из множества M = {1, 2, 3, 4} можно составить четыре различных сочетания из 4 по 3: {1, 2, 3}, {1,2,4}, {2, 3, 4}, {1, 3, 4}.
Число различных сочетаний из n элементов по k равно:


Учитывая, что число размещений из n элементов по k равно, но

можно выразить число сочетаний через число размещений, тогда получим:

Пример 9. Дано 10 точек, из которых никакие три не лежат на одной прямой и никакие четыре точки не лежат в одной плоскости. Сколько различных плоскостей можно провести через эти точки?
Из геометрии нам известна аксиома, что через три точки, не лежащие на одной прямой можно провести плоскость и притом только одну.
Поскольку это так, тогда, если плоскость проходит через три точки A, B, C, то через точки B, A, C или C, B, A и т.п., проходит та же плоскость, т. е.
порядок расположения трех точек, через которые проходит плоскость не имеет значения. А значит число различных плоскостей, проведенных через каждые три точки из 10 равно числу сочетаний из 10 элементов по 3.
Составим процедуру вычисления числа сочетаний из n элементов по k.
Для этого удобней воспользоваться второй формулой, в которой вычисляется только один факториал числа k. В формуле

Можно найти и другую формулу для числа сочетаний, в которой можно избежать больших чисел и вычисления факториалов чисел.


Итак, пользуемся формулой:

В процедуре, в качестве входных формальных переменных будут две переменные n и k, для числа всех элементов и числа выбираемых элементов.
Выходной параметр для значения сочетания обозначим c, имя процедуры - Сombination.
Получим: Procedure Combination(n, k : integer; var с : longint);
Входные параметры имеют тип integer, а выходной - longint, так как значение числа сочетаний может быть даже очень большим числом.
Переменные самой процедуры - i, - переменная для цикла for и p - промежуточная переменная для факториала k!.
В процедуре устанавливаются первоначальные значения для числа сочетаний (c := 1).
Организуется цикл for от 1 до k, в котором в переменную с будет накапливаться произведение, которое и является числом сочетаний из n элементов по k:


Давайте проверим, будет ли эта формула выдавать нам число сочетаний из n элементов по k. Пусть n = 5, k = 3, тогда по формуле для числа сочетаний будем иметь:

а по формуле (1), получаем:

Таким образом, этой формулой можно пользоваться при подсчете числа сочетаний в программе.
Окончательно процедура вычисления числа сочетаний будет следующей:
Procedure combination(n, k : integer; var
с : longint);
var
i : longint;
begin
с := 1;
for i := 1 to k do с := с*(n - k + i) div i
end;
Для составления программы решения данной задачи, надо в основной программе обратиться к процедуре combination, причем фактические значения переменных будут 10, - общее число точек и 3 - число точек через которые проходит одна плоскость.
Программа
Program Problem9;
uses WinCrt;
var
pl : longint;
{----------------------------------------------------------------------------------------}
Procedure combination(n, k : integer; var c : longint);
var
i : longint;
begin
c := 1;
for i := 1 to n - k do c := c*(n - k + i) div i
end;
{----------------------------------------------------------------------------------------}
begin
combination(10, 3, pl);
writeln('Число плоскостей равно: ', pl)
end.
Пример 10. Сколько различных вариантов хоккейной команды можно составить из 9 нападающих, 5 защитников и 3 вратарей, если в состав команды должны войти 3 нападающих, 2 защитника и 1 вратарь?
Соображения по составлению программы
Из 9 нападающих можно выбрать троих числом способов:




Программа
Program Problem10;
uses WinCrt;
var
h1, h2, h3 : longint;
{----------------------------------------------------------------------------------------}
Procedure Combination(n, k : integer; var c : longint);
var
i : longint;
begin
c := 1;
for i := 1 to k do c := c*(n - k + i) div i
end;
{----------------------------------------------------------------------------------------}
begin
combination(9, 3, h1);
combination(5, 2, h2);
combination(3, 1, h3);
write('Хоккейную команду можно составить ', h1*h2*h3);
writeln(' способами');
end.
Сочетания и бином Ньютона
В математике известна формула бинома (двучлена) Ньютона. Она используется для возведения двучлена a + b в n-ю степень. Эта формула имеет вид:

Числа

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Его можно записать иначе и сразу обозначить строки треугольника:
Номера строк. Треугольник Паскаля.
0 1
1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4 1
5 1 5 10 10 5 1
. . . . . . . . . . . . . . . . .
n

Пример 11. Вычислить сумму пяти средних элементов девятой строки треугольника Паскаля.
Всего в девятой строке треугольника Паскаля 10 элементов. Пять средних элементов будут находиться начиная с третьего места и по 7-е место.
Эти элементы будут следующими:

Ясно, что для вычисления их суммы необходимо организовать цикл по "верхним" индексам сочетаний. Каждый цикл надо вызывать процедуру числа сочетаний из 9 элементов по j (j - переменная цикла) и прибавлять к переменной, заведенной для суммы.
Программа
Program Problem11;
uses WinCrt;
var
s, j, s1 : longint;
{----------------------------------------------------------------------------------------}
Procedure Combination(n, k : integer; var c : longint);
var
i : longint;
begin
c := 1;
for i := 1 to k do
c := c*(n - k + i) div i
end;
{----------------------------------------------------------------------------------------}
begin
s := 0;
for j := 2 to 6 do
begin
combination(8, j, s1); s := s + s1
end;
writeln('Сумма пяти средних элементов 9-й строки равна ', s)
end.
Пример 12. Составить программу вывода на экран n заданных строк треугольника Паскаля.
Понятно, что для вывода строк треугольника Паскаля на экран необходимо организовать два цикла for. Один - по числу строк, второй - по числу элементов в каждой строке.
Первый, внешний цикл, для числа строк должен быть организован от 0 до n, пусть с переменной j1.
Второй, внутренний цикл, надо организовать от 0 до j1. Это легко объясняется тем, что в каждой строке должно быть на 1 больше элементов, чем номер ее строки. В нулевой строке 1 элемент, в 1-й 2 элемента, во 2-й три элемента и т. д., в n-й строке будет n + 1 элементов. Такое вызвано тем, что элементы начинают нумероваться с нуля.
Программа
Program
Problem12;
uses WinCrt;
var
j, j1, n, p : longint;
{----------------------------------------------------------------------------------------}
Procedure Combination(n, k : integer; var c : longint);
var
i : longint;
begin
c := 1;
for i := 1 to k do
c := c*(n - k + i) div i
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите число строк треугольника Паскаля ');
readln(n);
writeln('Треугольник Паскаля ');
for j1 := 0 to n do
begin
for j := 0 to j1 do
begin
combination(j1, j, p);
write(p, ' ')
end;
writeln
end
end.
Свойства математического ожидания как операции осреднения
Эти свойства справедливы для математических ожиданий случайных величин вообще и дискретных случайных величин, в частности.
1. Математическое ожидание постоянной равно этой постоянной:
MC = С.
2. Постоянный множитель C можно выносить за знак математического ожидания:
MCX = CMX.
3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
M(X + Y) = MX + MY.
Это свойство выражает линейность математического ожидания.
Математическое ожидание линейной комбинации случайных величин равно линейной комбинации их математических ожиданий.
Умножение математических ожиданий
Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.

и предпоследней цифр записи этого
1. Дано целое число n

2. Даны три числа a, b, c. Написать программу, в результате которой числа удвоятся, если

3. Составьте программы определения большего (меньшего) из трех чисел.
4. Написать программу, при выполнении которой выводится 1, если данное число x принадлежит отрезку [a, b], где a и b заданные числа, и выводится 0 в противоположной ситуации.
5. Точка плоскости задана своими координатами x, y. Написать программу, при выполнении которой определяется, принадлежит ли данная точка плоской фигуре, являющейся кольцом с центром в точке (0, 0), с внутренним радиусом 3 и с наружным радиусом 4.
6. Даны положительные числа x, y, z. Выяснить, существует ли треугольник с длинами сторон x, y, z?
7. Определить является ли данное целое число четным.
8. Определить, верно ли, что при делении целого неотрицательного числа a на целое положительное число b получается остаток r или s.
9. Составить программу решения биквадратного уравнения

10. Найти все трехзначные числа, при делении каждого из которых на 11 получается частное, равное сумме квадратов значений отдельных цифр данного числа.
11. Трехзначное десятичное число оканчивается цифрой 3. Если эту цифру переместить через два знака влево, т. е. с этой цифры будет начинаться запись нового числа, то это новое число будет на единицу больше утроенного исходного числа. Найдите это число.
12. Найдите все трехзначные числа, которые равны сумме кубов своих цифр.
13. Шестизначное десятичное число начинается слева цифрой 1. Если эту цифру перенести с первого места слева на последнее место справа, то значение образованного числа будет втрое больше исходного. Найдите исходное число.
14. Дано целое число

15. Найти четырехзначное число, равное квадрату числа, выраженного двумя последними цифрами этого четырехзначного числа.
16. Натуральное число называется совершенным, если оно равно сумме всех своих делителей, за исключением самого себя.
Число 6 является совершенным, так как 6 = 1 + 2 + 3, число 8 не является совершенным, так как 8 не равно 1 + 2 + 4. Написать программу вывода всех совершенных чисел, меньших заданного числа n.
17. Найти четырехзначные числа, каждое из которых делится на 11 и сумма цифр каждого равна 11.
18. Найти четырехзначные числа, которые, будучи приписаны справа к числу 400, дают полный квадрат.
19. Найти наименьшее целое число, делящееся на 7, которое при делении на 2, 3, 4, 5, 6 дает в остатке 1.
20. Какие числа, заключенные между числами 2320 и 2350 простые, а какие составные?
21. Составьте программу для нахождения наименьшего нечетного неравного 1 натурального делителя любого заданного натурального числа, большего 1.
22. Найти двузначное число, которое на 6 меньше квадрата суммы своих цифр.
23. Дана сократимая дробь, ее числитель и знаменатель - натуральные числа m и n. Найти такие натуральные числа m1 и n1, не имеющие общих делителей, что


24. Напишите программу, которая для каждого из целых чисел от 1 до n напечатает все его делители. Например, для числа 35 - делители: 1, 5, 7, 35. Аналогичный список делителей должен быть выдан для каждого из чисел от 1 до заданного числа n.
25. Найти наименьшее натуральное число n, обладающее следующими свойствами: а) его запись в десятичной системе счисления оканчивается цифрой 6;
б) если переставить цифру 6 из конца числа в его начало, то полученное число будет в 4 раза больше данного.
26. Написать программу вывода всех натуральных чисел, меньших n, квадрат суммы цифр которых равен m.
27. Можно ли данное целое p представить в виде суммы двух квадратов целых чисел? Написать программу решения этой задачи.
28. Найти все четырехзначные числа




29. Найти числа, оканчивающиеся на цифру a (a = 2, 3, 4, 5, 6, 7, 8, 9) и обладающее тем свойством, что если последнюю цифру переставить в начало числа, то число увеличится во столько раз, сколько единиц в переставляемом числе.
30. Найти целые числа n, делящиеся на все простые числа, не большие

31. Составьте программу для проверки, можно ли заданное натуральное число представить в виде:
а) произведения двух простых чисел; б) произведения трех простых чисел;
в) квадрата какого-либо простого числа; г) куба какого-либо простого числа. Следует напечатать ответ ДА или НЕТ.
32. Разрезание прямоугольника на квадраты.
61. Найти наибольший общий делитель всех чисел из заданного промежутка

62. Сократить дробь. Даны натуральные числа a и b. Сократить дробь

63. Найдите пять троек натуральных чисел (x; y; z), удовлетворяющих условию

64. Б. Кордемский указывает одно интересное число 145, которое равно сумме факториалов своих цифр: 145 = 1! + 4! + 5!. Он пишет, что неизвестно, есть ли еще такие числа, удовлетворяющие названному условию. Выясните, существуют ли еще такие числа?
65. Найти трехзначное число, являющееся точным квадратом числа a, и такое, чтобы произведение его цифр было равно a - 1.
66. Найти все натуральные решения уравнения в интервале [1; 20]

67. Найдите какие-нибудь три последовательных натуральных числа, каждое из которых делится на квадрат целого числа, большего единицы.
68. Нетрудно указать тройку квадратов целых чисел, образующих арифметическую прогрессию: 1, 25, 49. Найдите еще три такие тройки (из квадратов чисел, не имеющих общего делителя, т. е. взаимно простых).
69. Найти три таких простых числа, чтобы их сумма была в 5 раз меньше их произведения.
70. Попробуйте найти решения задачи Ферма

71. Попытайтесь найти пять идущих подряд целых чисел, таких, чтобы сумма квадратов двух наибольших из них равнялась сумме квадратов трех остальных?
72. Некоторое четное число является суммой двух точных квадратов. Докажите, что его половина является суммой двух точных квадратов.
73.

74. Пусть у целых чисел A и B последние k цифр одинаковы. Докажите, что у чисел


75. Покажите, что любое натуральное число и его пятая степень оканчиваются одной и той же цифрой.
76. Некоторое четное число является суммой двух точных квадратов. Докажите, что его половина является суммой двух точных квадратов.
77. Покажите, что квадрат числа, являющегося суммой двух точных квадратов, также можно представить в виде суммы двух точных квадратов.
78. Покажите, что произведение двух целых чисел, из которых каждое есть сумма квадратов двух целых чисел, можно представить в виде суммы двух точных квадратов.
79. Покажите, что n7- n делится на 42 (n - натуральное число).
80. Рассмотрим числа вида 22 + 1 (их называют иногда "числами Ферма"); при n = 2, 3, 4 мы получим числа 17, 257, 65537. Эти числа оканчиваются на 7. Докажите, что при любом натуральном n, больше 1, числа этого вида оканчиваются семеркой.
81. Сложили каких-то 3 целых числа, и их сумма разделилась на 6. Докажите, что сумма кубов тех же чисел также разделится на 6.
82. Покажите, что сумма квадратов двух нечетных чисел не может быть точным квадратом.
83. Число 365 нечетное. В то же время 365 можно представить в виде разности двух точных квадратов: 365 = 392 - 342 и 365 = 1832
- 1822. Докажите, что любое нечетное число можно представить в виде разности точных квадратов.
84. Целое число x заключено между 0 и 60 (0 < x < 60). При делении числа x на 3, 4, 5 получили соответственно остатки a, b, c. Докажите, что x равен остатку от деления числа 40a + 45b + 36c на 60. (На этом основан фокус - угадывания задуманного числа по остаткам от деления этого числа на 3, 4, 5.)
85. Число 148 делится на 37. Переставим в нем первую цифру с начала в конец: получится 481. Оно тоже делится на 37. Снова первую цифру (4) на последнее место. Опять получим число, которое делится на 37. Верно ли аналогичное свойство для каждого трехзначного числа, делящегося на 37?
86. Если дана последовательность 15 чисел a1, a2, a3, ..., a15, то можно построить новую последовательность чисел b1, b2, b3, ..., b15, где bi равно количеству чисел первой последовательности, меньших ai, i = 1, 2, ..., 15.
96. Сколько можно составить трехзначных чисел из нечетных цифр, если каждую из этих цифр использовать только один раз?
97. Сколько трехзначных чисел можно составить из всех цифр так, чтобы цифры в числах не повторялись?
98. Собрание, на котором присутствует 20 человек, избирает в президиум двух человек, один из которых должен быть председателем, а другой - секретарем. Каким числом способов это можно сделать?
99. Сколько различных слов, каждое из которых содержит 4 буквы, можно составить из букв слова выборка?
100. Сколько различных четырехзначных чисел можно написать при помощи цифр 0, 1, 2, ..., 9?
101. Сколько различных правильных дробей можно составить из чисел 3, 5, 7, 11, 13, 17, 19, 23?
102. Определить число всех диагоналей 5-, 8 -, 12 - и 15 - угольников?
103. Из двух спортивных обществ, насчитывающих по 100 фехтовальщиков каждое, надо выделить по одному фехтовальщику для участия в состязаниях. Сколькими способами можно это сделать?
104. У одного человека есть 7 книг по информатике, а у другого - 9 книг. Сколькими способами они могут обменяться друг с другом по две книги?
105. Для премий на олимпиаде по информатике выделено 3 экземпляра одной книги, два экземпляра другой и один экземпляр третьей книги. Сколькими способами могут быть вручены премии, если в олимпиаде участвовало 20 человек и никому не дают двух книг сразу? Та же задача, если никому не дают двух экземпляров одной и той же книги, но могут быть вручены две или три различные книги.
106. Во скольких точках пересекаются 8 прямых линий, если две из них параллельны между собой и через каждую точку пересечения проходит не более двух прямых?
107. Вычислить сумму четырех крайних членов одиннадцатой строки треугольника Паскаля.
108. Сколько хорд можно провести через 4 точки, лежащие на одной окружности?
109. На отрезке AB дано пять точек: C, D, E, F, K. Сколько различных отрезков, включая отрезок AB, получилось при этом?
110. Сколькими способами группу учащихся из восьми человек можно разбить на две подгруппы, состоящие из трех и пяти учеников.
111. Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну перчатку на правую руку так, чтобы эти перчатки были различных размеров?
112
Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти различных цветов?
113. Сколькими способами можно расставить белые фигуры (2 коня, 2 слона, 2 ладьи, ферзя и короля) на первой линии шахматной доски?
114. Найти число точек пересечения диагоналей, лежащих внутри выпуклого n-угольника, если никакие три из них не пересекаются в одной точке.
115. Известно, что при каждом взвешивании равновозможна как положительная, так и отрицательная ошибка. Какова вероятность того, что при пяти взвешиваниях получатся три положительные ошибки?
116. Из урны, содержащей белый и черный шары, извлекают шар, записывают его цвет и возвращают в урну. После n извлечений получаем кортеж длины n из букв Б и Ч. Какова вероятность, что он содержит k букв Б?
117. Для данного участника игры вероятность наброса кольца на колышек равна 0,3. Какова вероятность того, что при шести бросках кольца три кольца окажутся на колышке, если броски кольца считать независимыми?
118. Вероятность отказа каждого прибора при испытании равна 0,4. Что вероятнее ожидать: отказ двух приборов при четырех независимых испытаниях или трех приборов при шести испытаниях?
119. Партия изделий содержит 5% брака. Какова вероятность того, что среди взятых на испытание четырех изделий одно окажется бракованным?
120. Автоматическая штамповка металлических клемм для соединительных пластин дает 20% отклонений от принятого стандарта. Определить вероятность наличия в партии из 600 клемм от 100 до 125 клемм, не соответствующих стандарту.
121. Нужно исследовать 400 проб руды. Вероятность промышленного содержания металла в каждой пробе одинакова и равна 0.8. Определить вероятность того, что число проб с промышленным содержанием металла будет заключено между 290 и 350.
122. В каких границах находится частость наступления события при 1200 независимых испытаниях, вероятность отклонения которой от числа 2/3 равна 0.9857? Каковы границы частоты наступления события в этой задаче?
123. При массовом выпуске некоторой продукции бывает в среднем 4% брака. Определить вероятность того, что в партии из 625 единиц продукции отклонение частости от указанного процента брака будет менее, чем 0.02.
124. Средний процент нарушений работы кинескопа телевизора в течение гарантийного срока равен 12%. Вычислить вероятность того, что из 200 телевизоров более 160 выдержат гарантийный срок.
125. Посажено 600 семян кукурузы с вероятностью прорастания 0.9 для каждого семени. Найти границу абсолютной величины отклонения частости взошедших семян от вероятности p = 0.9, если эта граница должна быть гарантирована с вероятностью P = 0.995.
126. было посажено 400 деревьев. Найти вероятность того, что число принявшихся деревьев больше 250, если вероятность, что отдельное дерево приживется, равна 0.8.
127. В некоторой местности имеется 3 % больных малярией. Производится обследование 500 человек. С какой вероятностью среди обследованных окажется

Вероятность некоторого события равна 0.4 в каждом из n испытаний. Найти вероятность того, что:
а) Частость наступления события при n = 1500 отклонится от p = 0.4 в ту или другую сторону меньше, чем на 0.02.
б) Число появления события будет заключено между 1) 570 и 630; 2) 600 и 660; 3) 620 и 680; 4) 580 и 640.
в) В каких граница находится та частость события при n = 1200, вероятность отклонения которой от p = 2/3 равна 0.985? В каких границах заключено число появления событий в этой задаче?
г) Сколько необходимо произвести испытаний, чтобы вероятность того, что отклонение частости m/n от вероятности p = 3/8 в ту или другую сторону будет меньше, чем на 0.01, была равна 0.995?
128. Значение измеряемого теодолитом угла X имеет нормальное распределение со средним квадратическим отклонением, равным 8''. Найти вероятность того, что ошибка измерения угла не превзойдет по абсолютной величине 10''.
129. Станок автомат изготавливает валики. Контролируется их диаметр X. Считается, что X - нормально распределенная случайная величина со средним значением a = 10 мм. Какова средняя квадратическая ошибка, если с вероятностью 0.990 диаметр заключен в интервале (9.7; 10.3)?
130. В каких границах следует ожидать величину диаметра валика в предыдущей задаче с вероятностью 0.9973?
131. Случайная величина распределена по нормальному закону, Известно, что математическое ожидание ее равно 10 и среднее квадратическое отклонение равно 5. Определить вероятность того, что случайная величина примет значения, принадлежащие интервалу (7; 12).
132. Случайная величина распределена по нормальному закону. Ее математическое ожидание равно 10 и среднее квадратическое отклонение составляет 5. Определить вероятность того, что отклонение значений случайной величины от математического ожидания не превзойдет по абсолютной величине

133. Известно, что вес некоторых плодов, выращиваемых в совхозе, подчиняется нормальному закону с математическим ожиданием 175 г. и

134. Длина детали - случайная величина, распределенная по нормальному закону, со средним значением 20 см и дисперсией, равной 0.2 см2 . Определить вероятность того, что длина наудачу взятой детали будет заключена в пределах от 19.7 до 20.3 см.
135. При измерении расстояний до удаленных предметов ошибка подчинена нормальному закону со средним значением, равным 20 м и средним квадратическим отклонением 40 м. Определить вероятность того, что измеренное расстояние отклоняется от действительного в ту или иную сторону не более чем на 30 м.
136. Изготовленные цехом детали по размерам диаметра распределяются по нормальному закону с математическим ожиданием 4.9 см и средним квадратическим отклонением 0.5 см.
Условия в программах с циклами
Рассмотрим два примера, в программах которых используются не только циклы, но и в циклах необходимо применение условного оператора
if ... then ... else ...
Пример 3. Составить программу разложения натурального числа n на простые множители.
Прежде вспомним, что к простым числам относятся все те натуральные числа, которые имеют только два делителя - единицу и само себя.
Натуральные числа, имеющие более двух делителей называются составными.
Единица имеет только один делитель - само себя и поэтому она не может относится ни к простым, ни к составным числам. Если выписать простые числа в порядке их возрастания, начиная от самого меньшего - 2, то получим следующий ряд чисел:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...
А теперь вспомним, как в младших классах мы раскладывали натуральные числа на простые множители.
Для этого берем первое простое число - 2 и пробуем делить данное натуральное число на 2, если число делится на 2, тогда надо 2 записать, а число разделить на 2 и снова полученный результат пробуем делить на два, если делится, тогда повторяем процесс деления, если не делится, тогда пробовать делить на следующее простое число - 3 и так далее.
Обычно такой процесс мы записывали "столбиком":
Например: или


Таким образом, число 360 можно разложить на следующие простые множители: 360 = 2





Самый простой алгоритм для составления программы может быть таким.
Алгоритм
В качестве первого делителя взять 2, присвоить это значение некоторой переменной i;
начать цикл "пока i <= n";
если
данное число n делится на i, тогда выдать на экран значение i и разделив данное число на i, присвоить новое значение той же переменной n (n := n div i);
далее цикл продолжить, но значение i не увеличивать на 1, а проверить деление нового значения n на прежнее значение i;
если n не делится на i, тогда i увеличить на 1 (i := i + 1) и продолжить цикл, т.е.
выполнить проверку условия цикла (i <= n), а затем снова проверить деление n на уже новое значение i.
Обратите внимание, что при таком алгоритме в качестве делителей уже не попадут составные числа. Объясните почему?
Программа
Program
Problem3; { Разлож. числа на прост. множит.. 1- й спос. }
uses WinCrt;
var
n, i : integer;
begin
write('Введите натуральное число '); readln(n);
write('Простые делители числа ', n, ' следующие; ');
i := 2;
while i <= n do
if n mod i =0 then
begin
write(i, ' ');
n := n div i
end
else i := i + 1
end.
Конечно, эта программа далека от совершенства и не может иметь претензии на оригинальность.
Она заставляет компьютер выполнять много лишних проверок на деление.
Вот более совершенный алгоритм.
Он основывается на следующих соображениях.
Вначале находим все делители, равные 2. Для этого последовательно делим число 360 на 2:

После этого, полученный результат делим на нечетные числа. Причем на каждое нечетное число делим не один раз, а до тех пор, пока такое деление будет возможным.
Делим на 3: 45:3 = 15, 15:3 = 5.
Делим на 5: 5:5 = 1.
Делим на 7, не делится, пробуем делить на следующее нечетное число.
Делим на 9, не делится, переходим к следующему нечетному числу.
Делим на 11, не делится, и так далее.
До тех пор будем пробовать деление на нечетные числа, пока они будут меньше или равны получаемому частному от деления числа на соответствующий делитель.
На основании этих соображений составляем программу.
Program Problem3a;
uses WinCrt;
var
i, n : integer;
begin
write('Введите целое число '); readln(n); writeln;
writeln('Простые делители целого числа ', n);
{----------------------------------------------------------------------------------------}
while n mod 2 = 0 do { Цикл для вывода делителей, равных 2 }
begin
write(2, ' ');
n := n div 2
end;
{----------------------------------------------------------------------------------------}
i := 3;
while i <= n do { Цикл для нечетных делителей }
if n mod
i = 0
then
begin
write(i, ' ');
n := n div i
end
else i := i + 2;
writeln
end.
Можно расширить область вводимых чисел, используя уже известный тип
longint:
Еще один пример, где используются цикл и условие.
Пример 4. Написать программу, в результате выполнения которой выяснится, входит ли цифра 2 в запись данного целого числа n.
Идея составления программы проста. Надо организовать цикл, в котором выделять цифры числа уже известным вам способом и каждую из них сравнивать с цифрой 2. Если
цифра числа оказывается равной двум, тогда надо счетчик, которым может быть некоторая числовая переменная, увеличивать на единицу, иначе,
цикл надо продолжать.
Когда цикл будет выполнен полностью, т. е. все цифры числа проверены и каждая из них будет сравнена с цифрой 2, надо снова использовать условный оператор и сравнить значение переменной - счетчика с нулем. Если значение переменной равно нулю, то это значит, что цифра 2 не входит в запись числа, иначе
- входит.
АЛГОРИТМ
1. Содержание. Переменные целого типа n, p, k: n - для вводимого числа; p - для цифр этого числа; k - счетчик, подсчитывающий количество цифр в числе, равных 2.
2. Ввод целого числа.
Счетчику k устанавливается первоначальное значение 0.
3. Цикл, пока n <> 0. В цикле, переменной p присваивать значение цифры числа.
Если
p = 2, тогда увеличивать k на единицу.
Вычесть из числа n последнюю цифру и разделить его на 10.
Продолжить и закончить цикл.
4. Если
k = 0, тогда выдать сообщение: "Цифра 2 не входит в запись числа", иначе, выдать сообщение: "Цифра 2 входит в запись числа".
5. Конец.
Программа
Program
Problem4; { Входит ли цифра 2 в запись числа }
uses WinCrt;
var
n, p, k : integer;
begin
write('Введите целое число '); readln(n);
k := 0;
while n <> 0 do
begin
p := n mod 10;
if p = 2 then k := k + 1;
n := n div 10
end;
if
k = 0 then writeln('Цифра 2 не входит в запись этого числа')
else writeln('Цифра 2 входит в запись этого числа')
end.
Если вы внимательно разобрались в работе программы, то могли заметить, что во многих случаях в программе будет проделываться бесполезная работа.
Например, если нами введено число 31572. В программе сделано так, что отделяется по одной цифре справа и так продолжается до первой цифры слева.
Первой цифрой справа является 2. Казалось бы, раз в числе сразу первой цифрой найдена двойка, то можно выдать сообщение, что число содержит цифру 2 и на этом работу закончить. Однако в программе сделано не так. Цикл будет продолжаться до последней цифры числа и большая работа будет проделываться бесполезно.
Возникает необходимость в досрочном прерывании цикла. Как это сделать мы рассмотрим ниже.
Вещественный тип real в операторах if then else
Для дальнейшего составления программ на Паскале нам недостаточно целых чисел. Например, мы хотим составить программу решения квадратного уравнения вида:
ax2 + bx + c = 0.
Коэффициенты этого уравнения могут принимать не только целые значения, но любые действительные (a не равно нулю), также значения корней этого уравнения принимают значения из множества действительных чисел.
Действительные или вещественные числа объединяют в себе целые числа и дробные числа (рациональные и иррациональные).
Переменные, принимающие вещественные значения, имеют тип, который на языке Паскаль обозначается: real.
Например: var a, b, c : real;
Это означает, что переменные a, b и c принимают вещественные значения.
Второе определение непрерывной случайной величины
Величина X называется непрерывной случайной величиной, если вероятность попадания ее значения в любой интервал (x1, x2) может быть представлена в виде интеграла (2) от некоторой функции p(x) - плотности распределения вероятностей.

Плотность распределения вероятностей вполне определяет закон распределения непрерывной случайной величины X (или, как мы будем говорить, непрерывный закон распределения). При этом функция p(x) должна быть неотрицательной (что связано с не отрицательностью вероятностей) и должна быть нормирована условием

отражающим достоверность события


Плотность вероятности p(x) случайной величины X и ее функция распределения F(x) взаимно определяют друг друга. Действительно, если известна функция распределения F(x) случайной величины X, то плотность вероятности ее найдется по равенству (1). Наоборот, пусть известна плотность вероятности p(x) случайной величины X. Функция распределения F(x) определяется равенством:

Но согласно формуле (3) вероятность того, что случайная величина X примет какое-нибудь значение от


Из этих двух равенств получаем:

Таким образом, для полной характеристики случайной величины достаточно задать или функцию распределения, или плотность вероятности ее. Однако в большинстве случаев имеют дело с плотностью вероятности из-за удобств при теоретических исследованиях и из-за простых геометрических истолкований.
Выбор метода Оператор Caseof
Часто возникает необходимость сделать выбор из любого количества вариантов. В нашем случае такое может возникнуть, если пользователю необходимо выбрать из трех методов уточнения корня - один, по усмотрению пользователя, который, в свою очередь, выбирает метод в зависимости от заданной функции.
Структура оператора выбора в Turbo Pascale следующая:
Case I of
Const1 : S1;
Const2 : S2;
............
ConstN : SN;
else S
end;
В этой записи: I - выражение порядкового типа, значение которого вычисляется; Const1, Const2, ..., ConstN - константы, с которыми сравнивается значение выражения I; S1, S2, ..., SN - операторы, из которых выполняется тот, с соответствующей константой которого совпадает значение выражения I; S - оператор, который выполняется, если значение выражения I не совпадает ни с одной из констант Const1, ..., ConstN.
Ветвь оператора else является необязательной. Если она отсутствует и значение I не совпадает ни с одной из перечисленных констант, весь оператор рассматривается как пустой. В отличие от оператора if перед словом else точку с запятой можно ставить.
Если для нескольких констант нужно выполнить один и тот же оператор, их можно перечислить через запятую (или даже указать диапазон, если это возможно), сопроводив их одним оператором.
Пример 1
Program
Problem1; { Вычисление значений функций }
uses WinCrt;
var
i : integer;
x : real;
begin
{ Инструкция }
write('Введите значение аргумента '); readln(x);
writeln('Наберите соответствующий номер для');
writeln('вычисления значения нужной вам функции');
writeln('1 - sin(x), 2 - cos(x), 3 - exp(x), 4 - ln(x)');
readln(i);
Case I of
1 : writeln('Значение sinx = ', sin(x):1:8);
2 : writeln('Значение cosx = ', cos(x):1:8);
3 : writeln('Значение exp(x) = ', exp(x):8:8);
4 : writeln('Значение ln(x) = ', ln(x):8:8)
end
end.
Пример 2.
Case I of
0, 2, 4, 6, 8 : writeln('Четная цифра');
1, 3, 5, 7, 9 : writeln('Нечетная цифра');
10..100 : writeln('Числа от 10 до 100');
else
writeln('Отрицательное число или больше 100')
end;
Обратимся к поставленной задачи - выбора метода уточнения корня в зависимости от воли пользователя и особенностей заданной функции.
{ Основная программа }
begin
write('Введите левый конец промежутка a = '); readln(a);
write('Введите правый конец промежутка b = '); readln(b);
write('Введите точность вычисления корня eps = '); readln(eps);
writeln('Для выбора метода решения, введите его номер ');
writeln('1 - метод хорд, 2 - метод касательных');
writeln(' 3 - комбинированный метод'); readln(k);
Case
k of
1 : вызов процедуры метода хорд;
2 : вызов процедуры метода касательных;
3 : вызов процедуры комбинированного метода;
end;
writeln('Корень уравнения равен x = ', x:12:t(eps));
writeln('С точностью до eps = ', eps:1:t(eps))
end.
Но каждая из процедур должна претерпеть некоторые изменения, так как в предыдущих программа каждая из процедур, образно говоря, была менее независима от других конструкций программы, а теперь она должна быть полностью автономна.
{ Процедура уточнения корня методом хорд }
Procedure chord1(a, b, eps : real; var
x : real);
var
x1, min : real;
begin
minimum(a, b, eps, min);
x1 := a;
repeat
x := x1 - ((b - x1)*fx(x1))/(fx(b) - fx(x1));
x1 := x
until abs(fx(x))/min < eps
end;
Она названа Chord1, потому что в программе будет еще одна процедура под именем Chord, которая помогает в работе комбинированному методу.
Процедура вычисления корня по методу касательных может стать такой:
Procedure Tangent2(a, b, eps : real; var
x : real);
var
min : real;
begin
minimum(a, b, eps, min);
if fx(a)*derivat2(a, eps) > 0
then tangent1(a, b, eps, min, x)
else tangent1(b, a, eps, min, x)
end;
Она названа Tangent2, так как сама использует процедуру tangent1:
Procedure tangent1(a, b, eps, min : real; var x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - fx(x1)/derivat1(x1, eps);
x1 := x
until abs(fx(x))/min < eps
end;
А эта процедура названа tangent1, потому что процедура под именем tangent используется в работе комбинированного метода, процедура которого может быть такой:
{ Комбинированный метод }
Procedure Combination(a, b, eps : real; var x : real);
var
z : real;
begin
repeat
if fx(a)*derivat2(a, eps) > 0
then
begin
tangent(a, b, eps, z);
chord(b, a, x);
b := z; a := x
end
else
begin
tangent(b, a, eps, z);
chord(a, b, x);
b := x; a := z
end
until abs(z - x) < eps
end;
Разумеется в программе должны быть функции вычисления первой и второй производных, а также заданная функция.
Задание 3
Составьте полностью программу. Используйте ее для вычисления корней уравнений из предыдущего задания 2, выбирая метод в зависимости от уравнения и собственных соображений.
Вычисление корней уравнения нахождением минимума функции на промежутке
Зная определение минимума функции на промежутке, легко применить этот метод к нахождению корней уравнения.
Для этого достаточно рассматривать на заданном промежутке не саму функцию, а ее модуль, тогда минимум функции будет находиться на оси OX , а значение аргумента в этой точке даст нам значение корня уравнения на заданном промежутке. Разумеется, функция должна удовлетворять всем вышеперечисленным требованиям.
Ниже приводятся рисунки, которые наглядно показывают механизм применения поиска минимума функции на промежутке к нахождению корней. На одном из рисунков схематически показан график заданной функции, а на втором - график абсолютного значения этой функции применительно к нахождению корня с использованием поиска минимума для нахождения корня (см. рис. 28 и 29).
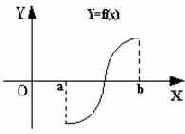
Рис. 28
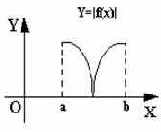
Рис. 29
Программа нахождения корня уравнения с использованием поиска минимума функции методом “золотого сечения” приводится ниже.
{Решение уравнений с использованием определения минимума }
{ с помощью "золотого сечения" }
Program Equation_min_gold;
uses WinCrt;
var
a, a1, b, b1, e, x : real;
{----------------------------------------------------------------------------------------}
{ Поиск минимума функции методом золотого сечения }
Procedure mingold(a, b, e : real; var
x : real);
var
x1, x2, y1, y2 : real;
{----------------------------------------------------------------------------------------}
Function func(x : real) : real;
begin
func := abs(sin(2*x) - ln(x))
end;
{----------------------------------------------------------------------------------------}
Function f1(a, b : real) : real;
begin
f1 := 0.618*a + 0.382*b
end;
{----------------------------------------------------------------------------------------}
Function f2(a, b : real) : real;
begin
f2 := 0.382*a + 0.618*b
end;
{----------------------------------------------------------------------------------------}
begin
x1 := f1(a, b); y1 := func(x1);
x2 := f2(a, b); y2 := func(x2);
while abs(b - a) > e do
if y1<y2 then
begin
b := x2; x2 := x1; y2 := y1;
x1 := f1(a, b); y1 := func(x1)
end
else
begin
a := x1; x1 := x2; y1 := y2;
x2 := f2(a, b); y2 := func(x2)
end;
x := (a + b)/2
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите нижнюю границу промежутка '); readln(a);
a1 := a;
write('Введите правую границу промежутка '); readln(b);
b1 := b;
write('Введите точность вычисления корня ');readln(e);
mingold(a, b, e, x);
write('Корень уравнения на промежутке (');
write(a1:1:0, '; ', b1:2:0, ')');
writeln(' равен x = ', x:6:6);
writeln('с точностью до ',e:2:6)
end.
Задание 5
Составьте программу нахождения корня уравнения, применяя поиск минимума функции с помощью ряда Фибоначчи.
Вызов процедуры из процедуры
Пример 7. Нумерация книжных страниц. В книге n страниц. Составим программу, которая будет находить, сколько цифр понадобится для того, чтобы занумеровать все страницы книги.
Решение
Математическое решение рассмотрим на частном примере, а потом сделаем общий вывод.
Пусть нам требуется определить число цифр для нумерации 357 страниц.
Естественными рассуждения будут такими: однозначных цифр 9, значит они пронумеруют 9 страниц; двузначных чисел 90 - они нумеруют 90 страниц и используют 90 .
2 = 180 цифр; трехзначных чисел 900 - они пронумеруют 900 страниц и используют 2700 цифр. Следовательно, для нумерации данных 357 страниц потребуются все однозначные и двузначные числа и часть трехзначных. Чтобы узнать, сколько трехзначных чисел потребуется для нумерации, надо из заданного числа вычесть "использованные" однозначные и двузначные числа: 357 - (9 + 90) = 258.
Итак, всего потребуется цифр:

. . . . . . . . . . .
Итого: 9 + 180 + 774 = 963 цифры.
Теперь обобщим наши соображения. Пусть задано число страниц n, которое имеет c
цифр. Тогда для нумерации потребуются цифры:
1 - значные; потребуется: 9

2 - значные; 90

3х - значные; 900

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c-1 -значные; 9....0 . (c-1) . . . цифр,
а c-значных полностью не хватит, также, как не хватило полностью трехзначных для нумерации 357 страниц.
Чтобы узнать сколько потребуется c-значных цифр, надо из данного числа вычесть все число одно, -дву, -трех,- и т. д., c-1 значные, которые уже использованы:

Попробуем на основе этих рассуждений составить программу.
Прежде, составим процедуру, которая определяет число цифр во введенном числе страниц. С такой программой мы уже раньше имели дело:
Procedure number(n : integer; var k : integer);
begin
k := 0;
repeat
k := k + 1;
n := n div 10
until n = 0
end;
В следующей процедуре будет находиться искомое число цифр. В ней, переменная m будет служить для указания числа цифр в одно, - двух, - трех, ... c-значных числах (9, 90, 900, ..., 9...0).
Переменная c
покажет число цифр в числе - номере страницы, в переменной z будет накапливаться искомый результат, а сумма s даст нам сколько всего n-значных чисел было использовано для подсчета.
Первоначальные значения: m := 9; z := 0; s := 0, а число цифр числа будет получено из процедуры number(n, c) и задаст значение переменной c:
m := 9; number(n, c); z := 0; s := 0;
Теперь организуем цикл по количеству цифр введенного числа страниц, от 1 до c - 1. Переменная цикла i.
for i := 1 to c - 1 do
begin
z := z + m*i; {Сумма цифр}
s := s + m;
m := m*10
end;
В цикле подсчитывается сумма цифр (z := z + m*i), сумма использованных однозначных, двузначных и т.д. цифр.
После завершения цикла, к сумме z добавляются оставшиеся c-значные цифры:
z := z + (n - s)

{цифрами}
Процедура
Procedure Page(n : integer; var
z : integer);
var
i, m, c, s : integer;
begin
m := 9;
number(n, c); z := 0; s := 0;
for i := 1 to c - 1 do
begin
z := z + m*i; {Сумма цифр}
s := s + m;
m := m*10
end;
z := z + (n - s)*c
end;
И, наконец, полностью программа
Program
Problem7; { Число цифр для нумерации страниц }
uses WinCrt;
var
n, c : integer;
{----------------------------------------------------------------------------------------}
Procedure number(n : integer; var k : integer);
begin
k := 0;
repeat
k := k + 1; n := n div 10
until n = 0
end;
{----------------------------------------------------------------------------------------}
Procedure Page(n : integer; var z : integer);
var
i, m, c, s : integer;
begin
m := 9; number(n, c); z := 0; s := 0;
for i := 1 to c - 1 do
begin
z := z + m*i; {Сумма цифр}
s := s + m; m := m*10
end;
z := z + (n - s)*c {n - s оставшиеся страницы c-значными цифрами}
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите число страниц '); readln(n);
page(n, c);
writeln(' Число цифр, необходимых для нумерации ', c)
end.
Задача Бюффона
Пример 5. На большой лист клетчатой бумаги со стороной клетки 1 случайно бросают точку. Какова вероятность, что она будет находиться на расстоянии меньше 1/2 от центра некоторой клетки?
Математическая схема решения
Достаточно рассмотреть одну клетку. Точки, находящиеся на расстоянии не более 1/2 от ее центра, заполняют круг площади


Эту задачу можно использовать для вычисления числа

Для этого задачу можно перефразировать так:
"На большой лист клетчатой бумаги со стороной клетки 1 случайно бросают точки. Вычислить значение числа

Для решения и этой задачи достаточно рассмотреть одну клетку.
Впишем в эту клетку окружность, радиус которой будет равен 1/2. Построим систему координат с началом в центре, вписанной в клетку окружности (см. рис. 35). Тогда площадь круга равна

Площадь квадрата равна S2 = 1.
Рис. 35
Как мы уже выяснили из предыдущей задачи вероятность того, что точка попадет в круг равна отношению площади круга к площади квадрата:

Мы можем "заставить" компьютер "бросать" в квадрат точки и подсчитать число всех точек и тех, которые попадут в круг.
Тогда вероятность определить просто, - надо будет найти отношение числа точек, попавших в круг к общему числу "брошенных" точек. Это значение и даст нам искомую вероятность.
Будем "бросать" в этот квадрат точки. Их координаты должны быть заключены в промежутке от -1/2 до 1/2 и могут задаваться функциями случайных чисел:
x := random - 1/2 и y := random - 1/2.
Координаты точек, которые попадают в круг должны удовлетворять неравенству:

Пусть общее число "брошенных" точек - n, а число точек попавших в круг - m, тогда, вероятность попадания точек в круг будет равна отношению числа точек, попавших в него, к общему числу брошенных точек: p := m/n.
Отсюда получаем, что S1/S2= m/n или

Таким образом, мы получаем способ для вычисления числа

Программа
Program Problem5;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Интегральная функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random - 1/2; y := random - 1/2;
if x*x + y*y <= 1/4 then m := m + 1
end;
p := 4*m/n;
writeln('Значение числа Pi равно ', p:8:6);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Пример 6. (задача Бюффона об игле). Плоскость разлинована на полосы шириной 1. На нее бросают иглу (отрезок) длиной 1. Какова вероятность, что игла пересечет одну из линий? (См. рисунки 36, 37 и 38).
Решение
У этой задачи удивительный ответ:


Наметим коротко одно из решений. Положение иглы (если не говорить о смещении ее вдоль линий, очевидно, не играющем роли) определяется двумя параметрами: расстояние y конца иглы от верхнего края полосы, в которую он попал


Рис. 36
Можно считать, по соображениям симметрии, что







полученной фигуры к площади S2 прямоугольника

Рис. 37
И тогда, вероятность того, что игла пересечет одну из линий будет равна:

С другой стороны, вероятность пересечения иглой одной из линий будет равна отношению числа пересечений к общему числу "бросаний" иглы: p = m/n. Приравнивая значения вычисленных вероятностей по первому и по второму способам, получим:


Выясним случайные координаты иглы, - угла

Как определить величину угла

Для этого расположим систему координат так, чтобы ее начало совпадало с концом иглы, ось OX была параллельна, проведенным прямым. Возьмем на игле две произвольные точки A и B, их координаты соответственно равны (x1, y1) и






Отсюда, значение угла


Чтобы игла пересекала хотя бы одну линию надо, чтобы y удовлетворял условию:


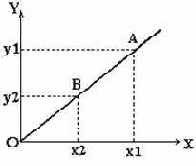
Рис. 38
Программа
Program Problem6;
uses WinCrt;
var
x1, x2, y1, y2, y, p, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Интегральная функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x1 := random; x2 := random;
y1 := random; y2 := random; y := random;
if y < cos(arctan((x1 - x2)/(y1 - y2))) then m := m + 1
end;
p := 2*n/m;
writeln('Значение числа Pi равно ', p:8:6);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Задание 19
Отрезок разделён на три равные части. Какова вероятность, что три точки, случайно брошенные на отрезок, попадут в три разные кусочка? Составьте программу.
Задача о встрече
Пример 4. Два лица A и B условились встретиться в определенном месте между 11 и 12 ч. Пришедший первым ждет другого в течение 20 мин, после чего уходит. Какова вероятность встречи этих лиц, если каждый в течение часа приходит к этому месту наудачу, а моменты прихода независимы друг от друга? (См. рис. 34).
Алгоритм решения
На прямой отложим отрезок, равный единицы длины, принимая за единицу масштаба 1 ч. Моменты случайного прихода лиц A и B можно изобразить точками на этом отрезке. Таким образом, нам необходимо выбрать наудачу две точки на данном отрезке. Обозначим моменты прихода лица A через x, а лица B - через y. Тогда множество всех возможных исходов испытания можно изобразить точками квадрата, сторона которого равна единице.
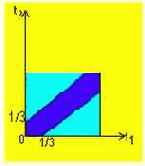
Рис. 34
Встреча произойдет лишь в том случае, если разность моментов прихода лиц A и B по абсолютной величине не будет превосходить 1/3 (20 мин), т.е. если произойдет событие, удовлетворяющее неравенству |x - y| < 1/3. Запишем это неравенство в виде системы неравенств:

Эта система неравенств задает область, заштрихованную на рисунке.
Программа
Program Problem4;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random;
y := random;
if (y > x - 1/3) and (y < x + 1/3) then
m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Задание 18
Составьте программы решения задач.
1. В соответствии с заданием на полет экипажам двух самолетов необходимо передать одно донесение по радио в любое время от 10 ч до 10 ч 15 мин. Для передачи донесения требуется 3 мин. Какова вероятность того, что радист одного самолета начнет передачу донесения тогда, когда радист другого самолета передачу своего донесения не закончит?
2. В течение 20 мин после 9 ч ученик A в случайный момент времени звонит по телефону ученику B и ждет 2 мин, после чего кладет трубку. В течение тех же 20 мин ученик B заходит в квартиру в случайный момент и остается дома в течение 5 мин. Какова вероятность того, что разговор между учениками состоится?
Задачи, решаемые с помощью размещений
Пример 3. Некто забыл нужный ему номер телефона, который состоит из одной из десяти букв и пяти цифр, но он помнит, что в образовании этого номера участвуют цифры 3, 5, 7, 9. Какое наибольшее количество проб надо сделать, чтобы дозвониться нужному абоненту?
В искомый номер должны войти четыре цифры, которые можно разместить на 5 местах


Комбинируя эти номера с каждой из десяти букв, получаем:
10



Составим программу
с использованием процедуры размещений.
Program Problem3;
uses WinCrt;
var
p : longint;
{----------------------------------------------------------------------------------------}
Procedure placement(n, k : integer; var r : longint);
var
i : integer;
begin
r := 1;
for i := 1 to k do
r := r*(n - k + i)
end;
{----------------------------------------------------------------------------------------}
begin
placement(5, 4, p);
p := 10*10*p;
writeln('Надо сделать ', p, ' проб, чтобы дозвониться')
end.
Пример 4. Сколько размещений из n элементов по m будет начинаться с первого элемента?
Соображения по составлению программы
Из n элементов выберем первый элемент и строго закрепим его на первом месте в получаемых размещениях.
Тогда, в исходном множестве останется n - 1 элементов, из которых надо выбирать еще по m - 1 - му элементу и добавлять к уже имеющемуся и стоящему на первом месте первому элементу.
Теперь остается выяснить, сколькими способами можно из n - 1 выбрать по


Поскольку первый элемент строго закреплен на первом месте в получаемых размещениях, то число всевозможных способов и будет равно

Программа
Program Problem4;
uses WinCrt;
var
p : longint;
m, n : integer;
{----------------------------------------------------------------------------------------}
Procedure placement(n, k : integer; var r : longint);
var
i : integer;
begin
r := 1;
for i := 1 to k do r := r*(n - k + i)
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите число всех элементов '); readln(m);
write('Введите число выбираемых элементов '); readln(n);
placement(m - 1, n - 1, p);
writeln('Число размещений из ', m, ' элементов по ', n, ',');
writeln('которые нач. с первого элемента, равно ', p)
end.
Пример 5. Составлены размещения из 10 элементов по 7 элементов. Сколько из этих размещений будут содержать: а) первый элемент, б) второй и четвертый элементы?
Решение
Во-первых, чем эта задача отличается от предыдущей?
В предыдущей задаче к первому элементу было строгое требование, - он должен находиться в образуемых размещениях обязательно на первом месте.
В этом примере, первый элемент просто должен присутствовать в получаемых размещениях, но совсем необязательно чтобы он находился на первом месте, значит он может занимать любое из 7 мест в получаемых размещениях.
Пронумеруем элементы множества цифрами от 1 до 7, тогда заданное множество элементов может быть записано так: {1, 2, 3, 4, 5, 6, 7}. Первый элемент выбираем из заданного множества, а "незанятые" места обозначим "x". Как видно, получается 7 подмножеств.

Отсюда следует, что его можно расположить в получаемых размещениях

Во-вторых,
после того, как "вытащили” первый элемент из 10 в нем осталось 9 элементов. Из этих 9 надо выбрать и добавить к первому элементу еще 6, чтобы всего получаемых эл. было бы 7. Это можно сделать


В итого мы имеем количество способов, равное произведению размещений

Программу
составьте самостоятельно
Задачи с использованием последовательностей и рядов
Пример 4. Последовательность (an)

задается так:


Найдите число, которое меньше всех членов последовательности с четными номерами и одновременно больше всех ее членов с нечетными номерами.
Если такое число существует, обозначим его a, тогда должно выполняться неравенство

Нетрудно заметить, что последовательность слева является возрастающей, а справа убывающей, а значит число a является "сгустком" для членов этой последовательности, т.е. ее пределом. Теперь осталось найти этот предел. Для этого воспользуемся признаком существования предела.
Зададимся положительным числом eps, даже очень малым и найдем члены последовательности, разность между которыми по абсолютной величине будет меньше eps. Найденный член последовательности и даст искомое число с указанной точностью.
Кстати говоря, это число в математике известно и равно

Программа
Program Problem4;
uses WinCrt;
var
n, k : integer;
a, a1, eps, e : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
begin
write('Задайте точность eps '); readln(eps);
a := 1;
repeat
a := 1 + 1/a; {с четными номерами}
a1 := 1 + 1/a {с нечетными номерами}
until abs(a1 - a) < eps;
write('Искомое число ', a1:3:t(eps));
writeln(' с точностью до ', eps:3:t(eps));
writeln('Сравните с точным результатом ', (sqrt(5)+1)/2:3:t(eps))
end.
Задание 4
Последовательность




Задачи с применением НОД
Пример 5. Один мастер делает на длинной ленте пометки синим карандашом от ее начала через каждые 36 см. Другой мастер делает пометки красным карандашом от начала через каждые 25 см. Может ли синяя пометка оказаться на расстоянии 1 см от какой-нибудь красной?
Решение
Ответ: может. Например, 9-я синяя пометка и 13-я красная находятся друг от друга на расстоянии 1 см, так как 13


В этой задаче нам фактически надо было найти какое-нибудь решение в целых числах одного из уравнений 25x - 36y = 1, 25x - 36y = - 1
или доказать, что таких решений нет. Существует стандартная процедура, с помощью которой всегда можно найти решение уравнения


36 = 25




Перепишем эту цепочку равенств по остаткам:
11 = 36 - 25




Тогда получим:
1 = 3 - (11 - 3






= 25






В результате получается равенство 25


Определение. Неопределенные уравнения - уравнения, содержащие более одного неизвестного.
Под одним решением неопределенного уравнения понимается совокупность значений неизвестных, которая обращает данное уравнение в верное равенство.
Уравнения вида ax + by = c, где a, b, c - целые числа, отличные от нуля
Теорема 1. Если НОД (a; b) = d, то существуют такие целые числа x и y, что имеет место равенство

(Это равенство называется линейной комбинацией или линейным представлением наибольшего общего делителя двух чисел через сами эти числа.)
Теорема 2. Если в уравнении ax + by = l (a, b) = 1, то уравнение имеет по крайней мере одно целое решение.
Справедливость этой теоремы следует из теоремы 1. Таким образом, чтобы найти одно целое решение уравнения ах + by = 1, если (а, b) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и b.
Пример. Найти целое решение уравнения 15x + 37y = 1.
Решение
1) Применим алгоритм Евклида и найдем НОД(15, 37):
НОД(15, 37) = 1
2) Выразим 1 последовательно через неполные частные и остатки, используя полученные равенства, начиная с конца:

x0
= 5, y0 = -2.
Теорема 3. Если в уравнении ах + by = с (а, b) = d > 1 и с не делится на d, то уравнение целых решений не имеет.
Пример. Найти целое решение уравнения 16x - 34y = 7.
Решение
(16, 34) = 2, 7 не делится на 2, уравнение целых решений не имеет.
Теорема 4. Если в уравнении ах + by = с (a, b) = d > 1 и c делится на d, то оно равносильно уравнению а1х + b1у = c1, в котором (a1, b1) = 1.
Теорема 5. Если в уравнении ах + by = с (а, b) = 1, то все целые решения этого уравнения заключены в формулах:

где x0, y0 - целое решение уравнения ах + by = 1, t - любое целое число.
Приведенные теоремы позволяют установить следующее правило решения в целых числах уравнения ах + by = с, где (а, b) = 1:
1) находится целое решение уравнения ах + by = 1 путем представления 1 как линейной комбинации чисел а и b (существуют и другие способы отыскания целых решений этого уравнения, например при использовании цепных дробей);
2) составляется общая формула целых решений данного уравнения:

где x0, y0 - целое решение уравнения ах + by = 1, t—любое целое число.
Придавая t определенные целые значения, можно получить частные решения данного уравнения: наименьшие по абсолютной величине, наименьшие положительные (если можно) и т. д.
Пример 1. Найти целые решения уравнения 407х - 2816у = 33.
Решение
1) Упрощаем данное уравнение, приводя его к виду 37х - 256у = 3.
2) Решаем уравнение 37x - 256y = 1.



3) Найдем решения данного уравнения по формулам:



Ответ:

Для составления программы решения неопределенных уравнений, нам предстоит решить три задачи:
1) нахождение НОД, для последующего выяснения числа решений уравнения, - это легко сделать с помощью известной процедуры;
2) нахождение одного решения уравнения вида ах + by = 1 и
3) последующий вывод обобщенных результатов решения с учётом знаков a и b, и с учетом формулы

Первую задачу можно решить с помощью рекурсивной функции:
Function nod(a, b : integer) : integer;
begin
if b = 0 then nod := abs(a)
else nod := nod(abs(b), abs(a) mod abs(b))
end;
Для решения второй задачи применять методику нахождения остатков от деления, а затем выполнять процесс в обратном порядке для компьютера нерационально. Проще составить два цикла с параметром, перебирающие числа от наименьшего (который равен наибольшему по модулю, но берётся с противоположным знаком) до наибольшего из коэффициентов (почему, будут существовать решения уравнения, меньшие или равные его коэффициентов? Докажите сами).
if abs(a) > abs(b) then max := abs(a) else max := abs(b);
for x := -max to max do
for y := -max to max do
Для вывода результатов следует рассмотреть несколько случаев, в зависимости от знаков коэффициентов a и b, а также, чтобы не получать несколько ответов, включить оператор безусловного перехода, после завершения проверки каждого условия.
Procedure
The_equation(a, b : integer); {Решение уравнения ax + by = 1}
label 1;
var
max, x, y, n : integer;
begin
if (nod(a, b) <> 1) then
writeln('Уравнение не имеет решений');
if abs(a) > abs(b) then
max := abs(a) else max := abs(b);
for x := -max to max do
for y := -max to x do
begin
if (a*x + b*y = 1) and
(a > 0) and (b > 0)
then begin writeln('Решения уравнения x = ', x, '+', b,'*t, y = ', y, '-', a, '*t,');
writeln('где t - произвольное целое число'); goto 1 end;
if (a*x + b*y = 1) and (a < 0) and (b > 0)
then begin writeln('Решения уравнения x = ', x, '+', b,'*t, y = ', y, ' ', a, '*t,');
writeln('где t - произвольное целое число'); goto 1 end;
if (a*x + b*y = 1) and (a > 0) and (b < 0)
then begin writeln('Решения уравнения x = ', x, ' ', b,'*t, y = ', y, '-', a, '*t,');
writeln('где t - произвольное целое число'); goto 1 end;
if (a*x + b*y = 1) and (a < 0) and (b < 0)
then begin writeln('Решения уравнения x = ', x, ' ', b,'*t, y = ', y, ' ', a, '*t,');
writeln('где t - произвольное целое число'); goto 1 end
end;
1: end;
Полностью программа решения уравнений вида ах + by = 1 будет такой:
Program Problem5;
uses WinCrt;
var
a, b : integer;
{---------------------------------------------------------------------------------------------------------}
Function nod(a, b : integer) : integer;
begin
if b = 0 then nod := abs(a)
else nod := nod(abs(b), abs(a) mod abs(b))
end;
{----------------------------------------------------------------------------------------------------------}
Procedure
The_equation(a, b : integer); {Решение уравнения ax + by = 1}
label 1;
var
max, x, y, n : integer;
begin
if (nod(a, b) <> 1) then
writeln('Уравнение не имеет решений');
if abs(a) > abs(b) then
max := abs(a) else max := abs(b);
for x := -max to max do
for y := -max to x do
begin
if (a*x + b*y = 1) and
(a > 0) and (b > 0)
then begin writeln('Решения уравнения x = ', x, '+', b,'*t, y = ', y, '-', a, '*t,');
writeln('где t - произвольное целое число'); goto 1 end;
if (a*x + b*y = 1) and (a < 0) and (b > 0)
then begin writeln('Решения уравнения x = ', x, '+', b,'*t, y = ', y, ' ', a, '*t,');
writeln('где t - произвольное целое число'); goto 1 end;
if (a*x + b*y = 1) and (a > 0) and (b < 0)
then begin writeln('Решения уравнения x = ', x, ' ', b,'*t, y = ', y, '-', a, '*t,');
writeln('где t - произвольное целое число'); goto 1 end;
if (a*x + b*y = 1) and (a < 0) and (b < 0)
then begin writeln('Решения уравнения x = ', x, ' ', b,'*t, y = ', y, ' ', a, '*t,');
writeln('где t - произвольное целое число'); goto 1 end
end;
1: end;
{-----------------------------------------------------------------------------------------------------------}
begin
write(' Введите значение коэффициента при x, a '); readln(a);
write('Введите значение коэффициента при y, b '); readln(b);
The_equation(a, b);
end.
в составление программы. Посудите сами,
1. Оператор goto
вносит фактическое безумие в составление программы. Посудите сами, какой человек может идти, идти, а затем без всякой причины повернуться и пойти обратно! У нормального человека всегда должна быть причина, условие
такого поступка.
Оператор goto
может заставить даже без всякой причины, условия нарушить естественный ход выполнения программы и перевести работу на помеченную строку.
Итак, оператор перехода изменяет последовательность выполнения операторов - они выполняются не в том порядке, как написаны в тексте программы. Операторы перехода нарушают связь между структурой выполнения (динамической) и текстовой (статистической) структурой программы.
Из-за этого программа становится менее понятной и труднее определяется ее правильность. Часто это становится гордиевым узлом, о котором программисты могут сказать: "Но все-таки программа работает". Почему и как работает программа, однако, остается секретом из-за оператора goto.
2. Частое использование операторов перехода указывает, что программист еще не научился программировать "структурно", т. е. использовать последовательные, разветвляющиеся и циклические структуры управления.
Оператор перехода рекомендуется использовать только в исключительных случаях. Такой случай может быть, когда цикл прерывается при удовлетворении определенного условия. Именно такой случай есть в нашей программе.
3. Переход внутрь сложного оператора не определен. Ошибок такого рода транслятор может и не обнаружить.
1) if
p then goto 3;
.....................
if q then 3: s;
2) while
i<= 10 do
begin
s1;
3: s2;
end;
.............
goto 3;
4. Метка в Турбо Паскале - это произвольный идентификатор (может быть обозначен и буквами), позволяющий именовать некоторый оператор программы и таким образом ссылаться на него.
В целях совместимости со стандартным языком Паскаль, в Турбо Паскале допускается в качестве меток использование целых чисел без знака.
Само собой возникает вопрос, можно ли программу примера 4 составить без оператора перехода goto?
Оказывается это возможно, о чем вы узнаете в следующих занятиях.