Арифметические операции с целыми числами и переменными целого типа в языке Паскаль
| Операция | Обозначение | ||
| Сложение | + | ||
| Вычитание | - | ||
| Умножение | * | ||
| Деление | a_div_b |
Знак "_" означает пробел. Пробелы между именами переменных и названием операции (div) - обязательны. (Происходит от английского division - деление).
Остаток от деления a на b. a_mod_b
Кроме арифметических операций с целыми числами выполняются:
Арифметические операции с вещественными переменными
| Операция | Запись на Паскале | ||
| Сложение | a + b | ||
| Вычитание | a - b | ||
| Умножение | a*b | ||
| Деление | a/b |
Как видите, единственным отличием от операций с целыми числами - это операция деления, которая обозначается наклонной чертой.
Кроме арифметических операций, в Паскале существуют так называемые стандартные
или встроенные функции, которые выполняются сразу после указания их имени, заведомо объявленных в Паскале, после которого в скобках записывается аргумент функции.
| Функция | Математическое
обозначение | Ее объявление на Паскале | |||
| Квадратичная |  | sqr(x) | |||
| Абсолютная величина | |x| | abs(x) | |||
| Квадратный корень |  | sqrt(x) | |||
| Синус | sinx | sin(x) | |||
| Косинус | cosx | cos(x) | |||
| Арктангенс | arctgx | arctan(x) | |||
| Натуральный логарифм | lnx | ln(x) | |||
| Показательная функция (экспонента) |  | exp(x) |
Некоторые из перечисленных встроенных функций могут быть использованы с целыми числами или переменными целого типа (аргумент имеет тип integer).
К таким функциям относятся:
Квадратичная: x2 - sqr(x). Абсолютная величина: |x| - abs(x).
На Паскале нет функций вычисления arcsinx, arccosx, arcctgx. Как с помощью уже известных встроенных функций вычислить значения функций arcsinx, arccosx, arcctgx?
Для этого надо совершить небольшую экскурсию в математику и выразить значение функций arcsinx, arccosx, arcctgx через функцию arctgx.
Arcsinx
Пусть






| Функция | Математическая обозначение | Ее объявление на Паскале | |||
| Арксинус | arcsinx |  |
Аналогичными рассуждениями можно получить выражения для arccosx и arcctgx.
| Функция | Математическое обозначение | Ее объявление на Паскале | |||
| Арккосинус | arccosx |  | |||
| Арккотангенс | arcctgx |  |
Пример 3. Составить программу решения квадратного уравнения
ax2 + bx + c = 0.
Наметим план составления программы или, иначе говоря, алгоритм.
Под алгоритмом мы будем понимать последовательность указаний для составления программы.
Алгоритм
1. Содержание.
Описание переменных и их типов.
2. Ввод
значений коэффициентов.
3. Вычисление
значения дискриминанта (d).
Если
d < 0, тогда уравнение не имеет корней,
иначе,
если d = 0,
тогда уравнение имеет один корень,
вычислить значение этого корня и выдать его на экран,
иначе, уравнение имеет два корня,
вычислить их и выдать на экран.
4. Конец.
Составим программу, пользуясь алгоритмом.
Program
Problem3; { Программа решения квадратного уравнения }
uses WinCrt;
var
a, b, c, d, x1, x2 : real;
begin
write('Введите коэффициенты уравнения ');
readln(a, b, c);
d := b*b - 4*a*c;
if d < 0 then writeln('Уравнение не имеет корней')
else
if d=0
then
writeln('Уравнение имеет один корень ',-b/(2*a))
else
begin
x1 := (-b - sqrt(d))/(2*a);
x2 := (-b + sqrt(d))/(2*a);
write('Уравнение имеет два различных корня ');
writeln('x1 = ', x1, ' x2 = ', x2)
end
end.
Разберем структуру программы и посмотрим как она будет работать.
ИМЯ ПРОГРАММЫ И КОММЕНТАРИЙ
Имя программы "Problem3;", после этого в комментарии записано содержание программы: "{Программа решения квадратного уравнения};".
РАЗДЕЛ ОПИСАНИЙ
В разделе описаний указаны имена переменных и их типы. Понятно, что переменные a, b, c нужны для значений коэффициентов уравнения, переменная d для значений дискриминанта, а x1 и x2 для корней уравнения. Понятно, что все они принимают вещественные значения, ограничиться целыми невозможно, и имеют тип: real.
РАЗДЕЛ ОПЕРАТОРОВ
Раздел операторов начинается вводом информации. С помощью оператора:
write('Введите коэффициенты уравнения '); readln(a, b, c);
на экран выводится информация, записанная в этом операторе write:
Введите коэффициенты уравнения
В ответ на этот запрос, пользователю надо ввести коэффициенты уравнения, разделяя их пробелами (проще говоря, ввести через пробелы).
Обратите внимание на такую мелочь, в операторе writeln, перед вторым, "заканчивающим" запись апострофом, оставлен пробел. Для чего? Только из эстетических соображений. Следующий оператор readln(a, b, c); будет вводить информацию, которую вы наберете с клавиатуры. Если этого пробела не будет, то вводимое число будет писаться вплотную к слову "уравнения", что, конечно, некрасиво.
Далее вычисляется значение дискриминанта и присваивается переменной d.
Первым условным оператором if проверяется условие d < 0, если оно выполняется, тогда на экран выдается сообщение, записанное после then в операторе writeln: "Уравнение не имеет корней", иначе после else, новое условие if
d = 0, тогда выполняются операторы после then, т.е. выдается сообщение, что уравнение имеет один корень, вычисляется его значение и выдается на экран, так как всё это записано в скобках оператора writeln, иначе, остается одно, - когда дискриминант больше нуля, тогда надо выполнить несколько операторов, которые записаны после else. Но поскольку их несколько, то необходимо открыть операторные скобки begin, в которых и записать вычисление значений корней и вывод их на экран. После чего необходимо закрыть операторные скобки служебным словом end.
После этого программа заканчивается служебным словом end с обязательной точкой в конце.
Каждая операторная скобка, начинаемая словом begin должна обязательно "закрываться" словом end. Если это слово оказывается перед оператором else или является предпоследним, то точка с запятой после end не ставится. Во всех других случаях end заканчивается точкой с запятой, а заканчивающий программу - точкой.
Бесконечные произведения
Напомним основные понятия, относящиеся к бесконечным произведениям.
Определение. Если


называют бесконечным произведением.
Станем последовательно перемножать числа (1), составляя частичные произведения

Эту последовательность частичных произведений

Предел P частичного произведения



называют значением
произведения (2) и пишут:

Если бесконечное произведение имеет конечное значение P и притом отличное от 0, то само произведение называют сходящимся, в противном случае - расходящимся.
Достаточно одному из сомножителей произведения быть нулем, чтобы и значение всего произведения также было равно нулю. В дальнейшем этот случай будет исключен из рассмотрения, так что для нас всегда

4.1. Примеры некоторых замечательных бесконечных произведений
Пример 1.

Так как частичное произведение

то бесконечное произведение сходится, и его значением будет

Проверим этот факт, для чего составим программу вычисления произведения:

Составим процедуру, которая с заданной точностью вычисляет это произведение и включим ее в программу. Зачем нам нужна процедура, если можно сразу составить программу?
Ответ понятен. Нам придется составлять еще много программ, в которых не только вычисляются произведения, но и выполняется ряд других задач. Изменив только одну процедуру, мы сможем использовать новое произведение для поставленных в программе задач.
Процедура
Procedure
Multiplication(eps : real; var Mult : real);
var
n : longint;
Mult1 : real;
begin
n := 2; Mult1 := 1;
repeat
Mult1 := Mult1*(1 - 1/sqr(n));
n := n + 1;
Mult := Mult1*(1 - 1/sqr(n))
until abs(Mult - Mult1) < eps
end;
Программа
Program Multiply1;
uses WinCrt;
var
Mult, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Procedure Multiplication(eps : real; var Mult : real);
var
n : longint;
Mult1 : real;
begin
n := 2; Mult1 := 1;
repeat
Mult1 := Mult1*(1 - 1/sqr(n));
n := n + 1;
Mult := Mult1*(1 - 1/sqr(n))
until abs(Mult - Mult1) < eps
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите точность вычисления '); readln(eps);
Multiplication(eps, Mult);
writeln('Значение произведения равно ', Mult:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
Пример 2.
4.2. Формула Валлиса (J. Wallis)
Формула Валлиса имеет для нас не только исторический интерес, но она поможет применять методику, которая будет использоваться при вычислении числа

Итак, формула Валлиса имеет вид:

или

Этот предел равносилен разложению числа


Она же приводит к формулам



Но надо заметить, что для вычисления числа

Составим процедуру, а затем и программу вычисления числа

Процедура
Procedure
Wallis(eps : real; var Mult : real);
var
n : longint;
Mult1 : real;
begin
n := 1; Mult := 1;
repeat
Mult := Mult*(4*sqr(n)/(4*sqr(n)-1));
n := n + 1;
Mult1 := 4*sqr(n)/(4*sqr(n)-1)
until Mult1 < eps
end;
Следует заметить, что оценка погрешности в этой процедуре отличается от оценки погрешности в процедуре примера 1. Такая оценка вытекает из математических соображений, n-й множитель в произведении Валлиса

Программа
Program Problem2;
uses WinCrt;
var
Mult, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Procedure Wallis(eps : real; var
Mult : real);
var
n : longint;
Mult1 : real;
begin
n := 1; Mult := 1;
repeat
Mult := Mult*(4*sqr(n)/(4*sqr(n)-1));
n := n + 1;
Mult1 := 4*sqr(n)/(4*sqr(n)-1)
until Mult1 < eps
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите точность вычисления '); readln(eps);
Wallis(eps, Mult);
writeln('Значение числа Пи равно ', 2*Mult:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
4.3. Полный эллиптический интеграл 1-го рода
Для полного эллиптического интеграла 1-го рода установлена формула

где переменная


Эта формула дает разложение K(k) в бесконечное произведение

Процедура
Procedure
Elliptic(k, eps : real; var Kk : real);
var
Kk1 : real;
begin
Kk1 := k;
repeat
k := (1 - sqrt(1 - sqr(k)))/(1 + sqrt(1 - sqr(k)));
Kk1 := Kk1*(1 + k);
k := (1 - sqrt(1 - sqr(k)))/(1 + sqrt(1 - sqr(k)));
Kk := Kk1*(1 + k);
until abs(Kk1 - Kk) < eps;
Kk := Kk*Pi/2
end;
Программа
Program Problem3;
uses WinCrt;
var
Kk, k, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Procedure Elliptic(k, eps : real; var
Kk : real);
var
Kk1 : real;
begin
Kk1 := k;
repeat
k := (1 - sqrt(1 - sqr(k)))/(1 + sqrt(1 - sqr(k)));
Kk1 := Kk1*(1 + k);
k := (1 - sqrt(1 - sqr(k)))/(1 + sqrt(1 - sqr(k)));
Kk := Kk1*(1 + k);
until abs(Kk1 - Kk) < eps;
Kk := Kk*Pi/2
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите значение k (0 < k < 1) '); readln(k);
write('Введите точность вычисления '); readln(eps);
Elliptic(k, eps, Kk);
writeln('Значение интеграла равно ', Kk:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
Задание 5
Известен предел:

Теперь мы можем записать это так:

В частности, при


Если вспомнить, что


Эта формула впервые была предложена Ф. Виетом (F. Viet) и является вместе с формулой Валлиса примерами первых бесконечных произведений.
Используя формулу (1) составьте программу вычисления числа

Библиотека часто встречающихся процедур и функций
1. Процедуры, вычисляющая сумму цифр числа:
Procedure sum_number(n : integer; var
s : integer);
begin
s := 0;
repeat
s := s + n mod 10;
n := n div 10
until n = 0
end;
Procedure sum_number(p : longint; var s : longint);
begin
s := 0;
while p <> 0 do
begin
s := s + p mod 10;
p := p div 10
end
end;
2. Процедура, вычисляющая количество цифр в числе:
Procedure quantity_number(n : integer; var
k : integer);
begin
k := 0;
repeat
k := k + 1;
n := n div 10
until n = 0
end;
3. Процедура, записывающая заданное число в обратном порядке, например, 3467 записывает так: 7643.
Procedure backwards(n : integer; var
a : integer);
begin
a := 0;
repeat
a := a*10 + n mod 10;
n := n div 10
until n = 0
end;
4. Процедура перестановки первой и последней цифр числа.
Procedure first_last_number(n : integer; var n1 : integer);
var
a, i, p : integer;
begin
a := n; i := 1;
p := n mod 10; {последняя цифра введенного числа}
while n >= 10 do
begin
i := i*10;
n := n div 10
end;
n1 := a - n*i - p + n + p*i
end;
5. Процедура, определяющая, является число числом - палиндромом.
Procedure palindrom(a : integer);
var
b, c, p : integer;
begin
b := a; c := 0;
repeat
p := b mod 10;
c := c*10 + p;
b := b div 10
until b = 0;
if c = a then writeln('Число ', a, ' является палиндромом')
else writeln('Число ', a, ' не явл.
29. Процедура размещений из n элементов по k элементов.
Procedure placement(n, k : integer; var
r : longint);
var
i : integer;
begin
r := 1;
for i := 1 to k do r := r*(n - i + 1)
end;
30. Процедура числа сочетаний из n элементов по k элементов.
Procedure Combination(n, k : integer; var c : longint);
var
i : longint;
begin
c := 1;
for i := 1 to k do
c := c*(n - k + i) div i
end;
41. Функция вычисляющая количество знаков после запятой.
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
42. Процедуры вычисления квадратного корня с заданной степенью точности.
1-й способ
Procedure square_root(u, eps : real; var
x : real);
begin
x := (u + 1)/2;
repeat
x := (1/2)*(x + u/x)
until abs(x*x - u) <= eps;
end;
2-й способ
Procedure square_root(u, eps : real; var
x : real);
var
x1, x2 : real;
begin
x1 := 1;
repeat
x1 := (1/2)*(x1 + u/x1);
x2 := (1/2)*(x1 + u/x1)
until abs(x2 - x1) <= eps;
x := x2
end;
Упражнения
167. Дано действительное число


Требуется получить все a1, a2, ..., меньшие или равные b.
168. Дано действительное


Найти первый отрицательный член последовательности a1, a2, ... .
169. Составить программу вычисления и вывода на экран n членов последовательности, заданной формулой n-го члена. (Предварительно составить рекуррентную формулу).
а)





е)




и)

170. Составить программу, подсчитывающую сумму n
первых членов последовательности, заданной формулой n-го члена. (Предварительно составить рекуррентную формулу).
а)




д)



з)



171. Дано действительное




Найти первый неотрицательный член последовательности.
172. Дано натуральное n. Вычислить:

173. Для чисел Фибоначчи u0, u1, ... справедлива формула Бине:

Так как

палиндромом')
end;
6. Процедура нахождения цифрового корня числа.
Цифровым корнем числа называется сумма цифр заданного числа, затем сумма цифр полученной суммы и т.д. до тех пор, пока эта сумма не станет однозначным числом.
Procedure radical_number(n : integer; var
k : integer);
var
p, s : integer;
begin
repeat
s := 0;
while n <> 0 do
begin
p := n mod 10; s := s+p; n := n div
10
end;
n := s
until n < 10;
k := n
end;
7. Процедуры нахождения наибольшего общего делителя:
1-й способ (по простому алгоритму)
Procedure nod1(a, b : integer; var
n : integer);
begin
if a > b then n := b else n := a;
n := n + 1;
repeat
n := n - 1
until (a mod n = 0) and (b mod
n = 0)
end;
2-й способ (по 1-му алгоритму Евклида)
Procedure nod2(a, b : integer; var
n : integer);
begin
while a <> b do
begin
if a > b then a := a - b else
b := b - a
end;
n := a
end;
3-й способ (по 2-му алгоритму Евклида)
Procedure nod(a, b : integer; var
n : integer);
var
r : integer;
begin
repeat
r := a mod b;
a := b; b := r
until b = 0;
n := a
end;
8. Рекурсивная процедура нахождения НОД.
Procedure nod(a, b : integer; var
n : integer);
begin
if b = 0 then n := a else nod(b, a mod
b, n)
end;
9. Процедуры нахождения наименьшего общего кратного двух целых чисел (НОК).
1-й способ
Procedure nok(a, b : integer; var
k : integer);
var
m, n : integer;
begin
k := 0;
repeat
if a > b then
begin
m := a; n := b
end
else
begin
m := b; n := a
end;
k := p + m
until k mod n = 0
end;
2-й способ (с использованием НОД).
Procedure nok1(a, b : integer; var
k : integer);
var
n : integer;
begin
n := a*b;
repeat
c := a mod b;
a := b; b := c
until b = 0;
k := n div a
end;
10. Процедура определения всех делителей заданного числа.
1-й способ
Procedure everyone_divisor(n : integer);
var
i : integer;
begin
writeln('Делители числа ', n);
for i := 1 to n div 2 do
if n mod i = 0 then write(i, ' ');
writeln(n)
end;
2-й способ
Procedure everyone_divisor(n : integer);
var
i : integer;
begin
writeln('Делители числа ', n);
for i := 1 to trunc(sqrt(n)) do
if n mod i = 0 then write(i, ' ', n div i, ' ')
end;
11. Процедура, определяющая число делителей натурального числа:
Procedure number_division(n : integer; var k : integer);
var
d : integer;
begin
k := 0;
for d := 1 to n div 2 do
if n mod d = 0 then k := k + 1;
k := k + 1
end;
12. Процедура разложения числа на простые множители:
Procedure probleme_number(n : integer);
var
i : integer;
begin
while n mod 2 = 0 do
begin
write(2, ' ');
n := n div 2
end;
i := 3;
while i <= n do
if n mod i = 0 then
begin
write(i, ' ');
n := n div i
end
else
i := i + 2
end;
13. Процедура, определяющая, является ли число простым.
первый
способ
Procedure probleme_number(p : integer);
var
i, k : integer;
begin
if p = 2 then write(p, ' ')
else
if p mod 2 <> 0
then
begin
i := 3; k := 0;
while i <= p div
2 do
begin
if p mod i = 0 then k := k + 1;
i := i + 2
end;
if k = 0 then
write(p, ' ')
end
end;
второй
способ
Procedure probleme_number(p : integer);
var
i, k : integer;
begin
if p = 2 then write(p, ' ')
else if p mod 2 <> 0
then
begin
i := 3; k := 0;
while i <= trunc(sqrt(p)) do
begin
if p mod
i = 0 then k := k + 1;
i := i + 2
end;
if k = 0 then
write(p, ' ')
end
end;
14. Процедура, определяющая, является ли число автоморфным? Автоморфным называется такое число, которое равно последним цифрам своего квадрата.
Например: 52 = 25; 252 = 625.
Procedura awtomorf(x : integer);
var
d, k : integer;
begin
d := 10;
while d <= x do d := d*10;
k := x mod 10;
if (k = 1) or (k = 5) or (k = 6)
then
if x*x mod d = x then
writeln(x, ' ', x*x)
end;
15. Процедура, устанавливающая, равно ли заданное число сумме квадратов целых чисел и каких именно, если таковые существуют:
Procedure square(n : integer);
label 1;
var
a, b, k : integer;
begin
a := 1; k := 1;
while a*a + 1 <= n do
begin
k := k + 1; a := a + 1
end;
for a := 1 to k do
for b := 1 to a do if a*a + b*b = n then
begin
writeln(n, '=', a, '*', a, '+', b, '*', b); goto 1
end;
1: end;
16. Процедура определения Пифагоровых чисел из промежутка [n; m].
Procedure pifagor(n, m : integer);
var
a, b, c : integer;
begin
writeln('Пифагоровы числа из промежутка [',n, ';', m,']');
for a := n to m do
for b := n to a do
for c := n to m do
if a*a + b*b = c*c then writeln(a, ' ', b, ' ', c)
end;
17. Процедура представления числа n в виде суммы кубов двух чисел.
Procedure sum_number_cube(n : integer; var p : integer);
var
i, j, k : integer;
begin
k := 0; i := 1;
while i*i*i + 1 <= n do
begin
k := k + 1; i := i + 1
end;
p := 0;
for i := k downto 1 do
for j := 1 to i do
if i*i*i + j*j*j = n
then
begin
p := p + 1;
writeln(i, '*', i, '*', i, '+', j, '*', j, '*', j, '=', n)
end;
if p = 0
then
begin
write('Число ', n, ' нельзя представить в виде ');
writeln('суммы кубов двух чисел')
end
else
writeln('Число способов равно ', p)
end;
18. Процедура представления целого числа n в виде суммы квадратов трех чисел.
Procedure sum_square_number(n : integer; var p : integer);
var
k, x, y, z, p : integer;
begin
k := 0; x := 1;
while x*x + 2 <= n do
begin
k := k + 1; x := x + 1
end;
p := 0;
for x := 1 to k do
for y := 1 to x do
for z := 1 to y do
if x*x + y*y + z*z = n
then
begin
p := p + 1;
writeln(x, '*', x, '+', y, '*', y, '+', z, '*', z, '=', n)
end;
if p = 0
then
begin
write('Число ',n,' нельзя представить в виде ');
writeln('суммы квадратов трех чисел')
end
else writeln('Число способов равно ', p)
end;
19. Процедура определения цифры, стоящей на n-ом месте в записи подряд чисел 1234567891011121314...
Procedure location(n : integer; var
c : integer);
var
p, s, v, m, q : integer;
Procedure number(n : integer; var k : integer);
begin
k := 0;
repeat
k := k + 1;
n := n div 10
until n = 0
end;
begin
p := 1; s := 0;
repeat
number(p, v);
s := s + v; p := p + 1
until s>=n;
m := s - n; p := p - 1; q := 1;
for i := 1 to m do q := q*10;
c := p div q;
c := c mod 10;
writeln('Последняя цифра в записи этих цифр будет ', c);
writeln('Она находится в числе ', p)
end;
20. Процедуры вычисления степени натурального числа с натуральным показателем:
с
циклом repeat ... until
...
Procedure extent(a, n : integer; var s : integer);
var
i : integer;
begin
i := 1; s := 1;
repeat
s := s*a; i := i + 1
until i = n
end;
с
циклом for ... to
... do ...
Procedure extent(a, n : integer; var s : longint);
var
i : integer;
begin
s := 1;
for i := 1 to n do s := s*a
end;
функция вычисления степени числа:
Function extent(a, n : longint) : longint;
var
i : integer;
begin
extent := 1;
for i := 1 to n do extent := extent*a
end;
21. Процедура вычисления факториала числа:
итеративная
Procedure fac(n : integer; var f : longint);
var
i : integer;
begin
if n = 0 then f := 1 else for i := 1 to n do f := f*i
end;
рекурсивная
Procedure fac(n : integer; var f : longint);
begin
if (n = 0) or (n = 1) then f := 1
else
begin
fac(n - 1, f);
f := f*n
end
end;
22. Рекурсивная процедура умножения числа a на каждую цифру числа b, начиная с единиц:
Procedure umnogenie(a, b, s : integer);
begin
if b <> 0
then
begin
s := s + a*(b mod 10);
umnogenie(a, b div 10, s div 10);
write(s mod 10:1)
end
else
if s <> 0 then write(s)
end;
23. Функции вычисления чисел ряда Фибоначчи.
итеративная
Function fib(n : integer) : integer;
var
f, f1, f2, i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1; f1 := f;
f := f1 + f2;
end;
fib := f
end;
рекурсивная
Function fib(n : integer) : integer;
begin
if (n = 1) or (n = 2)
then fib := 1
else fib := fib(n - 1) + fib(n - 2)
end;
24. Процедура отделения корней на заданном промежутке [a; b] для заданной функции fx, т.е. определения промежутков, на которых может находиться хотя бы один корень (h - шаг), (x1, x2 - границы полученных промежутков).
Procedure separation_root(a, b, h : real);
var
x1, x2, y1, y2 : real; k : integer;
Function fx(x : real) : real;
begin
fx := ???????????
end;
begin
k := 0; x1 := a; x2 := x1 + h;
y1 := fx(x1);
while x2 <= b do
begin
y2 := fx(x2);
if y1*y2 < 0
then
begin
k := k + 1;
writeln(k, '-й корень на [', x1:6:4, '; ', x2:6:4,']')
end;
x1 := x2; x2 := x1 + h;
y1 := y2
end
end;
25. Процедура уточнения корня некоторой функции func(x) методом деления пополам (a, b - границы промежутка, eps - точность вычисления, x - значение корня, d - погрешность вычисления).
Procedure half(a, b, eps : real; var
x, d : real);
var
c : real;
begin
while abs(b - a) > eps do
begin
c := (a + b)/2;
if func(a)*func(c) < 0 then b := c
else a := c
end;
x := (a + b)/2;
d := abs(b - a)/2
end;
26. Процедура поиском минимума функции на промежутка с помощью ряда Фибоначчи.
{ Процедура определения минимума функции на промежутке }
Procedure minfib(a, b, e : real; var x : real);
label 1;
var
aa, bb, x1, x2, y1, y2 : real;
n : integer;
{----------------------------------------------------------------------------------------}
{ Заданная исследуемая функция }
Function func(x : real) : real;
begin
func := ?????????????????
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления членов ряда Фибоначчи }
Function fib(n : integer) : real;
var
f, f1, f2 : real;
i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1; f1 := f;
f := f1 + f2
end;
fib := f
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления знач. аргумента и функции }
{ approach - приближение }
Procedure approach(a, b : real; n : integer; var
x2, y2 : real);
begin
x2 := a + (b - a)*fib(n - 1)/fib(n);
y2 := func(x2)
end;
begin
n := 3;
approach(a, b, n, x2, y2);
while abs(b - a) > e do
begin
x1 := a + b - x2; y1 := func(x1);
if (x2 > x1) and (y2 > y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
b := x2; x2 := x1; y2 := y1; goto 1
end;
if (x2 <= x1) and (y2 > y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
a := x2; x2 := x1; y2 := y1; goto 1
end;
if (x2 > x1) and (y2 < y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
a := x1; goto 1
end;
if (x2 <= x1) and (y2 <= y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
b := x1; goto 1
end;
n := n + 1;
approach(a, b, n, x2, y2);
1: end;
x := (a + b)/2;
end;
27. Процедура поиском минимума функции на промежутке с помощью “золотого сечения”.
Procedure mingold(a, b, e : real; var
x : real);
var
x1, x2, y1, y2 : real;
{----------------------------------------------------------------------------------------}
Function func(x : real):real;
begin
func := ????????????
end;
{----------------------------------------------------------------------------------------}
Function f1(a, b : real) : real;
begin
f1 := 0.618*a + 0.382*b
end;
{----------------------------------------------------------------------------------------}
Function f2(a, b : real) : real;
begin
f2 := 0.382*a+0.618*b
end;
{----------------------------------------------------------------------------------------}
begin
x1 := f1(a, b); y1 := func(x1);
x2 := f2(a, b); y2 := func(x2);
while abs(b - a) > e do
if y1<y2 then
begin
b := x2; x2 := x1; y2 := y1;
x1 := f1(a, b); y1 := func(x1)
end
else
begin
a := x1; x1 := x2; y1 := y2;
x2 := f2(a, b); y2 := func(x2)
end;
x := (a + b)/2
end;
28. Процедура решения неопределённых уравнений вида ax + by = c:
Procedure
The_equation(a, b, c : integer); {Решение уравнения ax + by = c}
label 1;
var
max, x, y, n : integer;
begin
if (nod(a, b) <> 1) and
(c mod nod(a, b) = 0)
then begin n:= nod(a,b); a := a div n; b := b div n; c := c div n end
else if (nod(a, b) <> 1) and (c mod nod(a, b) <> 0)
then
writeln('Уравнение не имеет решений');
if
abs(a) > abs(b) then max := abs(a) else max := abs(b);
for x := -max to max do
for y := -max to x do
begin
if (a*x + b*y = 1) and
(a > 0) and (b > 0)
then begin writeln('Решения уравнения x = ', x*c, '+', b,'*t, y = ', y*c, '-', a, '*t,');
writeln('где t - произвольное целое число'); goto 1 end;
if
(a*x + b*y = 1) and (a < 0) and (b > 0)
then begin writeln('Решения уравнения x = ', x*c, '+', b,'*t, y = ', y*c, ' ', a, '*t,');
writeln('где t - произвольное целое число'); goto 1 end;
if
(a*x + b*y = 1) and (a > 0) and (b < 0)
then begin writeln('Решения уравнения x = ', x*c, ' ', b,'*t, y = ', y*c, '-', a, '*t,');
writeln('где t - произвольное целое число'); goto 1 end;
if
(a*x + b*y = 1) and (a < 0) and (b < 0)
then begin writeln('Решения уравнения x = ', x*c, ' ', b,'*t, y = ', y*c, ' ', a, '*t,');
writeln('где t - произвольное целое число'); goto 1 end
end;
1: end;

Вычислить и округлить до ближайшего целого все числа

а также вычислить u0, u1, ..., u15 по формулам


174. Вычислить и вывести на экран положительные значения функции

175. Вычислить значения функции


176. Вычислить члены ряда



Определить a128, если известны r и а4.
178. Вычислить и вывести на печать значения членов ряда




179. Вычислить значения функции

180. Последовательность an принимает значения

Чему равен предел an при

181. Установите, имеет ли следующая последовательность un предел?

182. Показать, что последовательность


183. Установить имеет ли последовательность, заданная формулой n-го члена предел: а)


б)



Таким образом, xn+1 получается из xn по формуле

в)

Ответы
К заданию 3
Program Task3;
uses WinCrt;
var
n : integer;
y, eps : real;
{----------------------------------------------------------------------------------------}
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until
eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Procedure
Element_succession(eps : real; var n : integer; var y : real);
var
k : integer;
begin
n := 1;
y := 1;
k := -1;
while abs(y - 2) >= eps do
begin
n := n + 1;
k := k*(-1);
y := 2 + k/n
end
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
writeln('Введите любое положительное число');
write(' Можно даже очень малое '); readln(eps);
Element_succession(eps, n, y);
writeln('Искомый член последовательности ', y:6:t(eps));
writeln('Находится на ', n , '-ом месте')
end.
К
заданию 4
Program Task4;
uses
WinCrt;
var
i, j, n : integer;
k, k1 : longint;
yn, ym, eps : real;
{----------------------------------------------------------------------------------------}
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until
eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
begin
writeln('Введите любое положительное число ');
write('Можно даже очень малое '); readln(eps);
i := 1;
yn := 1/3;
k := 2;
while
abs(yn - 1) >= eps do
begin
i := i + 1;
k := k*2;
yn := (k - 1)/(k + 1)
end;
writeln('Условию |yn - 1| < ', eps:1:t(eps), ' удовлетворяет');
writeln('член последовательности yn = ', yn:6:t(eps), ',');
writeln('находящийся под номером ', i); writeln;
write('Введите номер члена последовательности ');
write('больше ', i, ' '); readln(n);
j := i; ym := yn;
k1 := k;
while
j <= n do
begin
j := j + 1;
k1 := k1*2;
ym := (k1 - 1)/(k1 + 1);
end;
if
abs(ym - 1) < eps
then
begin
write('Неравенство abs(1 - ',ym:6:t(eps),') <', eps:1:t(eps));
writeln(' выполняется')
end
else
begin
write('Неравенство abs(1-', ym:6:t(eps),') <', eps:1:t(eps));
writeln(' не выполняется')
end
end.
К заданию 5
Program Task5;
uses
WinCrt;
var
n : longint;
u, u1, eps : real;
{----------------------------------------------------------------------------------------}
Function
s(k : integer) : longint;
var
i, z : longint;
begin
z := 1;
for
i := 1 to k do z := 3*z;
s := z
end;
{----------------------------------------------------------------------------------------}
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until
eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
writeln('Задайте положительное число eps');
write(' Можно даже очень малое '); readln(eps);
u := 0;
n := 1;
repeat
u := u + 1/(s(n) + 1);
n := n + 1;
u1 := u + 1/(s(n) + 1);
until
abs(u1 - u) < eps;
writeln('Предел последовательности равен ', u1:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
Биномиальное распределение
Пример 1. В урне находятся белые и черные шары. Доля белых шаров в урне равна p. Случайное событие А заключается в том, что вынутый наугад шар будет белого цвета; вероятность этого случайного события равна p - доле белых шаров в урне. Вынув из урны шар, отмечают, белый он или нет, затем вынутый шар возвращают в урну и шары тщательно перемешивают. После этого снова вынимают наугад один шар и так повторяют n раз.
Случайная величина X - это число появлений события А, т.е. белого шара, при n-кратном повторении испытания. Возможными значениями величины X являются числа 0, 1, 2, ..., n (0 - белый шар не появляется ни разу при всех n испытаниях, 1 - белый шар появляется один раз, 2 - два раза, ..., n - раз, т.е. во все испытаниях).
Найдем закон распределения вероятностей случайной величины X.
Событие X = n означает появление события А во всех испытаниях; по правилу умножения вероятностей (с учетом условия независимости испытаний) получим

Аналогично находим


Событие X = m (m = 1, 2, ..., n-1) означает, что за n испытаний случайное событие А наступит точно m раз, а значит противоположное событие наступит n - m раз.
Вероятность того, что событие А наступит в первых m испытаниях и не наступит в остальных n - m испытаниях, подсчитаем по правилу умножения вероятностей:

Эта вероятность не зависит от того, в каких именно испытаниях наступит событие А. Поэтому по правилу сложения вероятностей искомая вероятность




Здесь

| X | 0 | 1 | ... | m | ... | n-1 | n | ||||||||
| P(X=m) |  |  | ... |  | ... |  |  |
Этот закон распределения называется биномиальным законом распределения вероятностей. Название связано с тем, что вероятности совпадают с членами разложения бинома (q + p)n по степеням p:

Для вычисления вероятностей по формуле (1) придется не только возводить в степень, но и вычислять число сочетаний из n элементов по k. При этом могут быть достаточно большие числа, что даже установив их вещественный тип можем выйти за пределы допустимого диапазона и получить ошибку при работе программы на Турбо Паскале. Чтобы избежать этого, составим рекуррентное соотношение, с помощью которого можно вычислять вероятности.
Вероятность P(X = m) равна

а вероятность P(X = m - 1) вычисляется по формуле

Разделим левые и правые части этих равенств, получим:


Таким образом, начиная с P(X = 0), вероятности P(X = m) могут быть вычислены по следующей рекуррентной формуле:


Теперь, для вычисления вероятностей достаточно вычислить вероятность при m = 0, а затем воспользоваться приведенным соотношением.
При m = 0 получаем

Для возведения в натуральную степень вещественного числа составим процедуру:
{ Процедура возведения в степень }
Procedure Extent(a : real; n : integer; var e : real);
var
i : integer;
begin
e := 1;
if
n = 0 then e := 1
else
for i := 1 to n do e := e*a
end;
Используя эту процедуру нетрудно составить процедуру вычисления вероятностей, используя рекуррентное соотношение. Она может быть построена как итеративно, так и рекурсивно. Итеративная процедура приводится ниже, а рекурсивную составьте самостоятельно.
{ Рекуррентная процедура вычисления вероятности }
{биномиального закона распределения }
Procedure
Recurro_binomial(n, m : integer; p : real; var pp : real);
var
i : integer;
begin
Extent(1 - p, n, pp);
for
i := 1 to m do pp := (pp*(n - i + 1)*p)/(i*(1 - p))
end;
Используем эти процедуры для решения следующей задачи.
Пример 2. Из большой партии изделий берут на пробу 10 штук. Известно, что доля нестандартных изделий во всей партии составляет 25 %.
Требуется найти вероятность того, что более пяти отобранных изделий окажутся нестандартными.
Математическое решение задачи
Отбор каждого изделия будем считать испытанием, а обнаружение нестандартности у отобранного изделия - событием А. Вероятность p события А равна доле нестандартных изделий во всей партии, т. е. p = 0.25.
Количество X нестандартных изделий среди отобранных будет случайной величиной с биномиальным распределением вероятностей, если только изделия для пробы отбираются по схеме случайной повторной выборки (изделие после проверки возвращается обратно в общую партию). При этом вероятности подсчитываются по формуле (1) при n = 10, p = 0.25, q = 1 - 0.25 = 0.75.
По правилу сложения вероятностей складываем вероятности при m = 6, 7, 8, 9, 10 и находим искомую вероятность P(X > 5).
Программа
{ Биномиальный закон распределения вероятностей }
Program Problem2;
uses WinCrt;
var
p, pp, sum : real;
n, i : longint;
{----------------------------------------------------------------------------------------}
{ Процедура возведения в степень }
Procedure Extent(a : real; n : integer; var e : real);
var
i : integer;
begin
e := 1;
if n = 0 then e := 1 else for i := 1 to n do
e := e*a
end;
{--------------------------------------------------------------------------------------}
{ Рекуррентная процедура вычисления вероятности }
{ биномиального закона распределения }
Procedure Recurro_binomial(n, m : integer; p : real; var pp : real);
var
i : integer;
begin
Extent(1 - p, n, pp);
for i := 1 to m do pp := (pp*(n - i + 1)*p)/(i*(1 - p))
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите число всех изделий '); readln(n);
write('Введите вероятность появления нестандартного изделия '); readln(p);
writeln('Биномиальный закон распределения вероятностей'); writeln;
for i := 0 to n do write(i:6, ' '); writeln;
writeln;
sum := 0;
for i := 0 to n do
begin
Recurro_binomial(n, i, p, pp);
write(pp:1:4, ' ');
if i >= 6 then sum := sum + pp;
end;
writeln; writeln;
writeln('Вероятность того, что более пяти отобранных');
writeln('изделий окажутся нестандартными равна ', sum:1:6)
end.
Блок-схемы, изображающие условные операторы
Вы уже знаете, что составление программы можно изображать геометрическими фигурами - блоками, в результате чего образуется схема программы. Такая конструкция называется блок-схемой.
Какой геометрической фигурой принято обозначать условие? Посмотрите на ниже приведенную конструкцию и вы увидите, что условие изображается ромбом (см. рис. 17).

Рис. 17
Пример 4. Два прямоугольника заданы длинами сторон. Написать программу, после выполнения которой выясняется, можно ли первый прямоугольник целиком разместить во втором. (Рассмотреть только случай, когда соответствующие стороны прямоугольников параллельны.)
Математика этой задачи проста, возможные случаи изображены на рисунке 18, блок-схема на рис. 19:
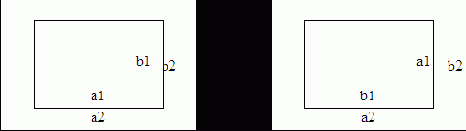
Рис. 18
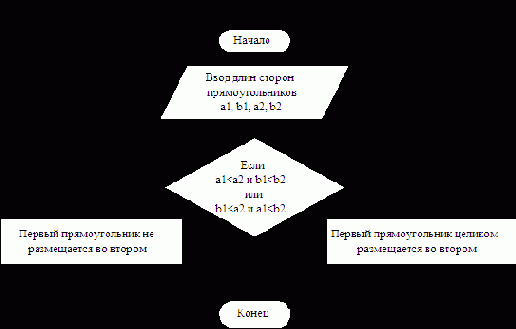
Рис. 19
Пользуясь блок-схемой составим программу
Program Problem4;
uses WinCrt;
var
a1, b1, a2, b2 : real;
begin
write('Введите длину и ширину первого прямоугольника ');
readln(a1, b1);
write('Введите длину и ширину второго прямоугольника ');
readln(a2, b2);
if ((a1 < a2) and (b1 < b2)) or
((b1 < a2) and (a1 < b2))
then writeln('Первый прямоугольник размещается во втором')
else writeln('Первый прямоугольник не размещается во втором')
end.
Целый тип longint
Турбо-Паскаль имеет возможности для расширения диапазона значений целых переменных.
Так, если тип integer устанавливает диапазон целых значений от -32768 до 32767, то целый тип longint расширяет его от -2147483648 до 2147483647.
Итак, если установить тип переменных longint, тогда выше приведенные программы будут работать для значительно большего множества целых чисел.
Программы
станут такими:
Program
Problem1; { Опред. и вывод на экран цифр числа }
uses WinCrt;
var
n, p, i : longint;
begin
write('Введите натуральное число n '); readln(n);
i := 1;
while n <> 0 do
begin
p := n mod 10;
writeln(i, ' - я цифра справа равна ', p);
n := n div 10;
i := i+1
end
end.
Program Sum; { Сумма цифр числа }
uses WinCrt;
var
a, n, s, p : longint;
begin
write('Введите натуральное число n '); readln(n);
a := n; s := 0;
while n <> 0 do
begin
p := n mod 10; {Определяются цифры числа}
s := s + p; {Находится их сумма}
n := n div 10
end;
writeln('Сумма цифр числа ', a, ' равна ', s)
end.
Program
Problem2a; { Перест. первой и последней цифр числа }
uses WinCrt;
var
n, n1, p, a, i : longint;
begin
write('Введите натуральн. число n <= 2147483647 ');
readln(n);
a := n;
i := 1;
p := n mod 10; {последняя цифра введенного числа}
while n >= 10 do
begin
i := i*10;
n := n div 10;
end;
n1 := a - n*i - p + n + p*i;
writeln('Число после перестановки цифр ', n1);
end.
Подведем итог о
целых типах.
Диапазон возможных значений целых типов зависит от их внутреннего представления, которое может занимать один, два или четыре байта. В таблице приводятся названия целых типов, длина их внутреннего представления в байтах и диапазон возможных значений.
Целые типы
|
Длина, байт |
Название типа |
Диапазон значений |
|
1 |
byte |
0 ... 255 |
|
1 |
shortint |
-128 ... 127 |
|
2 |
word |
0 ... 65535 |
|
2 |
integer |
-32768 ... 32767 |
|
4 |
longint |
-2147483648 ... 2147483647 |
Целый тип данных относится к порядковым типам, которые отличаются тем, что каждый из них имеет конечное число возможных значений. Эти значения можно определенным образом упорядочить и, следовательно, с каждым из них можно сопоставить некоторое целое число - порядковый номер значения (отсюда название типов - порядковый).
Вещественные типы, строго говоря, тоже имеют конечное число значений, которое определяется форматом внутреннего представления вещественного числа. Однако количество возможных значений вещественных типов настолько велико, что сопоставить с каждым из них целое число (его номер) не представляется возможным.
Порядковый
и вещественный типы, в свою очередь, относятся к простым типам.
Числовые характеристики биномиального распределения
При подсчете математического ожидания и дисперсии биномиального распределения воспользуемся методом математической индукции.
Для упрощения расчетов представим случайную величину X - число успехов при n-кратном повторении испытания - в виде суммы более простых величин. В качестве таких величин возьмем индикаторы успехов: 1 - "успех", 0 - "неудача". Таким образом, индикатор Xk принимает значение 1 в случае успеха при k-ом повторении испытания и значение 0 в противном случае. Поэтому
X = X1 + X2
+ ... + Xn,
так как эта сумма состоит из единиц и нулей, причем число единиц в ней равно числу успехов при n-кратном повторении испытания.
Отсюда следует, что
MX = MX1 + MX2
+ ... + MXn
(в силу свойства линейности математического ожидания).
Так как биномиальное распределение связано с последовательностью независимых испытаний по схеме Бернулли, то индикаторы X1, X2, ..., Xn
- независимые случайны величины; поэтому можно применить и теорему сложения дисперсий, что дает
DX = DX1 + DX2
+ ... + DXn.
По условию задачи вероятность успеха при каждом повторном испытании одна и та же и равна p. Поэтому распределение вероятностей любого индикатора Xk
дается таблицей
 | 1 | 0 | |||
| p | q |
где q = 1 - p; k = 1, 2, ..., n.
Непосредственный подсчет математического ожидания и дисперсии индикатора Xk приводит нас к следующему результату:


Следовательно, для биномиального распределения имеем
MX = np,
DX = npq,
и, значит,

Математическое ожидание и дисперсия относительной частоты X/n:


Мы пришли к очень важному, применительно к программированию, выводу.
Математическое ожидание относительной частоты случайного события есть вероятность этого события. Формула среднего квадратического отклонения показывает, что рассеяние относительной частоты уменьшается с увеличением числа повторений испытания.
Пример 3. Составить закон распределения случайной величины, выражающей число попаданий в мишень при четырех выстрелах, если вероятность попадания при каждом выстреле равна 0.3.
Вычислить ее математическое ожидание и дисперсию по формулам для характеристик случайной величины, распределенной по биномиальному закону.
{ Биномиальный закон распределения вероятностей }
Program Problem3;
uses WinCrt;
var
p, pp, mx, dx : real;
n, i : integer;
{-------------------------------------------------------------------------------------}
{ Процедура возведения в степень }
Procedure Extent(a : real; n : integer; var e : real);
var
i : integer;
begin
e := 1;
if
n = 0 then e := 1
else
for i := 1 to n do e := e*a
end;
{---------------------------------------------------------------------------------------}
{ Рекуррентная процедура вычисления биномиального закона }
{ распределения }
Procedure
Recurro_binomial(n, m : integer; p : real; var pp : real);
var
i : integer;
begin
Extent(1 - p, n, pp);
for i := 1 to m do pp := (pp*(n - i + 1)*p)/(i*(1 - p))
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите число выстрелов '); readln(n);
write('Введите вероятность попадания при каждом выстреле '); readln(p);
writeln('Биномиальный закон распределения вероятностей');
writeln;
for
i := 0 to n do write(i:6, ' '); writeln;
for
i := 0 to n do
begin
Recurro_binomial(n, i, p, pp);
write(pp:1:4, ' ')
end;
writeln;
mx := n*p;
dx := n*p*(1 - p);
writeln('Математическое ожидание, т.е. число попаданий ');
writeln('при четырех выстрелах ', mx:4:6);
writeln('Дисперсия равна ', dx:4:6);
writeln('Среднее квадратическое отклонение ', sqrt(dx):4:6)
end.
Пример 4.
Длительной проверкой установлено, что из каждых 10 приборов 8 - точных. Составить таблицу распределения числа точных приборов из взятых наудачу пяти приборов. Вычислить математическое ожидание и дисперсию.
{ Биномиальный закон распределения вероятностей }
Program Problem4;
uses WinCrt;
var
p, pp, mx, dx : real;
n, i : integer;
{----------------------------------------------------------------------------------------}
{ Процедура возведения в степень }
Procedure Extent(a : real; n : integer; var e : real);
var
i : integer;
begin
e := 1;
if
n = 0 then e := 1
else
for i := 1 to n do e := e*a
end;
{----------------------------------------------------------------------------------------}
{ Рекуррентная процедура вычисления биномиального закона }
{ распределения }
Procedure
Recurro_binomial(n, m : integer; p : real; var pp : real);
var
i : integer;
begin
Extent(1 - p, n, pp);
for i := 1 to m do pp := (pp*(n - i + 1)*p)/(i*(1 - p))
end;
{---------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите число взятых наудачу приборов '); readln(n);
p := 0.8;
writeln('Вероятность появления точного прибора ', p:1:6);
writeln('Биномиальный закон распределения вероятностей');
writeln;
for
i := 0 to n do write(i:6, ' '); writeln; writeln;
for
i := 0 to n do
begin
Recurro_binomial(n, i, p, pp);
write(pp:1:4, ' ')
end;
writeln; writeln;
mx := n*p; dx := n*p*(1 - p);
writeln('Математическое ожидание, т.е. число точных ');
writeln('приборов из взятых наудачу пяти ', mx:4:6);
writeln('Дисперсия равна ', dx:4:6);
writeln('Среднее квадратич. отклонение ', sqrt(dx):4:6)
end.
Числовые характеристики распределения Пуассона
Математическое ожидание

Это позволяет выяснить статистический смысл параметра a в распределении Пуассона: параметр a есть среднее число событий, наступающих за время t в простейшем потоке. Отсюда можно дать статистическое толкование параметру



Дисперсия равна

Дисперсия совпадает с математическим ожиданием. Эти результаты хорошо согласуются с представлением распределения Пуассона в качестве предельного для биномиального распределения при

Действительно, при этом MX = np = a, DX = npq = a(1 - p)

Что такое цикл?
Давайте отвлечемся на некоторое время от программирования и попытаемся на природных явлениях, примерах из повседневной жизни человека, а затем и его мыслительной деятельности дать понятие цикла.
Если вас спросят, что такое цикл, то, наверное, вы не задумываясь ответите, что это повторяемость
чего-то.
И это совершенно правильно!
Повторяемость времен года в природе - это цикл, кругооборот воды в природе - это цикл, смена дня и ночи - это цикл и многие другие процессы в природе повторяются, образуя циклы или, что чаще нами употребляется, цикличность.
Циклы в математике - явление очень часто встречающееся.
Например, пока
натуральные числа меньше 10, тогда надо суммировать их.
Другими словами, мы находим сумму чисел от 1 до 10.
В этом примере повторяется сложение натуральных чисел, пока выполняется условие
(числа меньше 10).
Такие циклы называются циклами с предыдущим условием или, коротко, с предусловием, потому что условие записывается перед выполнением повторяющейся группы операторов.
Цикл в программировании - это многократно выполняемая группа команд, часть программы.
Сразу заметим, что в программе может быть такая ситуация, когда цикл вообще не выполняться ни разу.
На языке Паскаль возможны циклы с предусловием, которые организуются с помощью оператора:
while (пока) ... do (выполнять) ...
Формат оператора: while <условие> do <операция>.
Работа оператора заключается в том, что операция выполняется до тех пор, пока будет выполняться условие, указанное в операторе while.
Если операция содержит не один оператор, а несколько, то их объединяют с помощью ОПЕРАТОРНЫХ СКОБОК begin и end, например;
while <условие> do
begin
S1; S2; S3; ...
end;
В этом примере символами s1, s2, s3, ... обозначены операторы.
Действие цикла while
... do ... можно изобразить графически следующей схемой (см.
рис. 20):
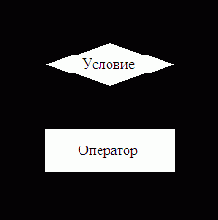
Рис. 20
Рассмотрим работу оператора while ... do ... на примере.
Пример 1. Определить и вывести на экран цифры целого числа n.
Разберем математику этого вопроса на частном примере.
Найдем цифры числа 4538. Для этого надо найти остаток от деления 4538 на 10 с помощью операции нахождения остатка от деления целых чисел (mod):
4538 mod 10 = 8, получим последнюю цифру числа (она же является первой справа).
Выдаем сообщение: "1 - я цифра справа равна 8".
После этого выполним целочисленное деление заданного числа 4538 на 10, получим 453 (остаток отбрасывается):
4538 div 10 = 453.
Далее процесс повторяем:
2 - й раз; 453 mod 10 = 3
2 - я цифра справа равна 3,
453 div 10 = 45,
3 - й раз; 45 mod 10 = 5,
3 - я цифра справа равна 5,
45 div 10 = 4,
4 - й раз; 4 mod 10 = 4,
4 - я цифра справа равна 4,
4 div 10 = 0.
Обратите внимание! Процесс будет продолжаться пока
число n не равно нулю. Как только оно станет равно нулю цикл заканчивается.
В программе еще надо указывать какая по счету цифра в числе справа. Для этого надо завести еще одну переменную в качестве счетчика. Эта переменная каждый цикл должна увеличиваться на 1.
Программа
Program
Problem1; {Опред. и вывод на экран цифр числа.}
uses WinCrt;
var
n, p, i : integer;
begin
write('Введите натуральное число n <= 32767 '); readln(n);
i := 1;
while n <> 0 do
begin
p := n mod 10;
writeln(i, ' - я цифра справа равна ', p);
n := n div 10;
i := i + 1
end
end.
Построение
программы и ее работа.
В разделе описаний
Переменная n для целого числа, p - для цифр числа, i - счетчик цифр.
В разделе операторов
С помощью оператора write выводится на экран запрос для пользователя о вводе целого числа. Оператор readln заносит его значение в память и присваивает переменной n.
Счетчику i устанавливается первоначальное значение 1.
В операторе while записывается условие (пока n не равно 0), при котором цикл будет выполняться.
Так как в цикле несколько операторов, то используются операторные скобки
begin ... end.
В них записаны операторы:
p := n mod 10; - определяется последняя цифра;
writeln(i,' - я цифра справа равна ', p); - выводится на экран порядковый номер цифры справа и сама эта цифра;
n := n div
10; - от числа "зачеркивается" последняя цифра;
i := i + 1; - счетчик увеличивается на 1.
Циклы в циклах
Рассмотрим еще один пример, где уже приходиться использовать два цикла, один внутри другого.
Пример 5. Составить программу вывода всех натуральных чисел, меньших n, квадрат суммы цифр которых равен заданному числу m.
Сущность задачи такова. Вводится натуральное число, до которого надо выводить все натуральные числа, удовлетворяющие заданному условию. Пусть, например, пользователь введет число - 21.
Второе число, которое надо ввести пользователю - это число, которому равен квадрат суммы цифр натуральных чисел.
Понятно, что это число должно быть точным квадратом, оно может быть: 4, 9, 16, 25, 36 и т.д.
Допустим, что пользователь ввел число 4.
Надо найти все натуральные числа от 1 до 21, квадрат суммы цифр которых равна 4. Начинаем из чисел: 1, 2, 3, 4, 5, ..., 21, выбирать те, которые удовлетворяют заданному условию.
Первое из них - 2, так как 22 = 4, второе - 11, так как (1 + 1)2 = 22
= 4, третье - 20, так как (2 + 0)2 = 22 = 4.
Других натуральных чисел до 21, удовлетворяющих такому условию нет.
Все отобранные числа надо вывести на экран, т. е. 2, 11 и 20.
Алгоритм
1. Раздел описаний.
Переменные: n, m, k, a, p, s. Тип целый.
n - для границы значений натуральных чисел, m - для числа, с которым сравнивается квадрат суммы цифр (точный квадрат), k - для натуральных чисел от 1 до n, a - для запоминания натурального числа, перед тем, как будет определяться сумма его цифр, p - для цифр числа, s - для суммы цифр.
2. Раздел операторов.
Ввод значений n и m. Установить первоначальное значение для k (эта переменная "перебирает" все натуральные числа от 1 до n, k := 1).
Цикл, пока
k <= n.
В цикле: установить первоначальные значения для суммы s (s:=0); запомнить число в переменную a (a := k).
Цикл для подсчета суммы цифр, пока k <> 0.
В цикле: выделять по одной цифре числа, известным способом; прибавлять по одной цифре к сумме; уменьшать число на последнюю цифру и на порядок.
Закончить цикл для подсчета суммы цифр.
Проверка выполнения условия.
Если
квадрат суммы цифр равен заданному числу,
тогда
вывести это натуральное число на экран.
Перейти к проверке следующего числа.
Закончить основной цикл проверки чисел.
3. Закончить программу.
По этому алгоритму составим программу.
Program Problem5;
uses WinCrt;
var
n, m, k, a, p, s : integer;
begin
write('Введите натуральное число, до которого ');
write('выводить искомые числа '); readln(n);
writeln('Введите число, с которым сравниваете квадрат');
write('его суммы цифр. Оно должно быть точн. квадрат. '); readln(m);
write('Искомые числа: ');
k := 1;
while k <= n do
begin
s := 0; a := k;
while k <> 0 do
begin
p := k mod 10;
s := s + p;
k := k div 10
end;
if sqr(s) = m then write(a, ' ');
k := a + 1
end
end.
В программе два цикла. Один - внешний, для натуральных чисел, второй - внутренний, для подсчета суммы цифр числа.
Дискретная случайная величина, закон распределения вероятностей
Под случайной величиной мы будем понимать величину, значение которой изменяется случайным образом от одного испытания к другому.
Определение. Величина X называется дискретной случайной величиной, если множество ее возможных значений представляет собой конечную или бесконечную последовательность чисел x1, x2, x3, ..., xi, ... и если каждое событие X = xi является случайным событием, т.е. имеет определенную вероятность pi
(события X = xi мы будем называть элементарными событиями).
Примерами дискретных случайных величин являются: число X выпадений герба при бросании двух монет; число X очков, выпадающих на верхней грани игральной кости; число вынутых из урны белых или черных шаров, если в ней содержится определенное число белых и черных шаров; число стандартных изделий в определенной партии изготовленных изделий и др.
Законом распределения (вероятностей) случайной величины X мы будем называть любое правило или закон, позволяющее находить все вероятности

Как и любую функцию ее можно задать различными способами: словесным описанием, таблицей, формулой, графиком.
Пример 1. Число X выпадений герба при бросании двух монет есть дискретная случайная величина, закон распределения вероятностей которой можно задать таблицей:
| X | 0 | 1 | 2 | ||||
| P | 1/4 | 1/2 | 1/4 |
Если случайная величина X может принимать лишь конечное число различных значений x1, x2, x3, ..., xk, то их вероятности образуют полную группу случайных событий, и поэтому сумма их вероятностей равна единице:
p1 + p2
+ ... + pk = 1.
Если множество (различных) возможных значений величины X бесконечно, то конечную сумму в этой формуле можно заменить на бесконечный ряд сумма которого тоже равна 1.

Пример 2. Число X очков, выпадающее на верхней грани правильной игральной кости, есть дискретная случайная величина с законом распределения, записанным таблицей
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
|
P |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
Дисперсия, среднее квадратическое отклонение и другие характеристики рассеяния
Математическое ожидание MX называют центром распределения случайной величины. Обозначим MX = a.
Тогда рассеянием случайной величины X называется отклонение X - a этой величины от ее центра a. Чем больше эта разность, тем больше рассеяние случайной величины от MX.
Непосредственный подсчет математического ожидания этой разности равен нулю M(X - a) = MX - a = 0, и поэтому не может быть числовой характеристикой рассеяния случайной величины.
Основной числовой характеристикой рассеяния случайной величины X служит среднее квадратическое отклонение


Расчеты удобнее производить с подкоренным выражением, которое получило специальное название дисперсии случайной величины X и обозначают DX:
DX = M(X - a)2
Таким образом, дисперсия есть средний квадрат отклонения случайной величины от ее центра распределения. Эта величина уже дает большие возможности для оценки случайной величины и нахождения закона распределения ее вероятности.
Для вычисления дисперсии может быть применима формула:
DX = M(X - a)2
= M(X - C)2 - (a - C)2 ,
где C - любое число. В частности, при C = 0 получаем:
DX = MX2 - a2 = MX2 - (MX)2
Для дополнительных занятий
Пример 14. Сколько всех делителей у числа 210? У числа 30030? У целого числа n?
Первая
мысль, которая возникает, - это делить заданное натуральное число на простые числа и подсчитать число простых делителей. Остальные делители получаются всевозможными сочетаниями из простых делителей. Значит, возникает необходимость подсчитать число таких сочетаний, причем сочетания должны быть различными.
Но такой путь является достаточно сложным и долгим. Более простой путь решения можно избрать, если знать следующее математическое утверждение.
Пусть p1, ..., pm - различные простые делители числа q. Если



Основываясь на этом предложении составим программу.
Алгоритм
для составления программы может быть таким:
1.
Определяется число простых делителей, равных 2.
2. Число этих делителей увеличивается на 1 и присваивается переменной s.
3. Определяется число нечетных простых делителей.
4. Для каждого простого нечетного делителя устанавливается их число, увеличивается на 1 и умножается на s.
5. Результат - число всех делителей выводится на экран.
Программа
Program Problem14;
uses WinCrt;
var
s, q, m, j, n : integer;
begin
write('Введите целое число '); readln(n);
m := n;
q := 0;
s := 0;
while m mod 2 = 0 do
begin
q := q + 1;
m := m div 2
end;
s := q + 1; j := 3; q := 0;
while j <= m do
begin
if m mod j =0 then
begin
q := q + 1;
m := m div j
end;
s := s*(q + 1);
if m mod j <> 0 then j := j + 2
end;
writeln('К-во всех делителей числа ', n, ' равно ', s)
end.
Дополнительные задания
Пример 9. Задача об остроугольном треугольнике. На окружности случайно выбираются три точки. Какова вероятность того, что треугольник с вершинами в этих точках - остроугольный? (См. рис. 41).
Решение
Ясно, что при любом повороте окружности вероятности событий и условие "остроугольности" сохраняются; так что мы можем считать, что одна из трех выбираемых вершин A, B, C - скажем, C - фиксирована, а две другие уже выбираются случайно. Будем задавать их положения величинами дуг CA = a, CB = b, отсчитываемых против часовой стрелки. Будем измерять дуги в радианах, тогда пара (a, b) - это точка в квадрате 0 < a < 2Pi, 0 < b < 2Pi. По теореме о том, что величина вписанного угла измеряется половиной дуги между его сторонами, углы треугольника ABC равны Pi-b/2, a/2 и (b-a)/2 (мы считаем, что b>a; случай a>b совершенно аналогичен - a и b меняются ролями). Точки (a, b) в треугольнике a<b<Pi, для которых все три угла A, B, C меньше Pi/2, т.е. b>Pi, a<Pi и b-a<Pi, заполняют внутренность меньшего треугольника, образуемого средними линиями большего. Ситуация в нижнем треугольнике b<a<Pi симметрична относительно диагонали a=b квадрата. Поэтому искомая вероятность равна
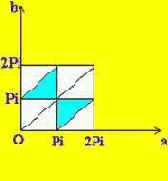
Рис. 41
Program Problem9;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m : longint;
{-------------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{-------------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{-------------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random*2*pi; y := random*2*pi;
if ((y > pi) and (y < x + pi) and (x < pi)) or
((y < pi) and (y > x - pi) and (x > pi))
then m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
155. На отрезке [0; 1] случайно выбираются три числа. Какова вероятность того, что а) выбранное последним число наибольшее? б) числа идут в порядке возрастания?
Пример 10. Какова вероятность того, что при двух бросаниях кубика выпадут а) два числа с суммой не меньше 10? б) два числа, из которых первое делится на второе?
Идея решения задачи проста. Каждое из двух бросаний мы смоделируем, как получение двух случайных чисел из промежутка [1; 6]. (Число очков на игральном кубике следующее: 1, 2, 3, 4, 5, 6).
Для получения таких чисел можно использовать функции:
x := random(6) + 1 и y := random(6) + 1.
"Бросать" кубик будем не два раза, а количество бросаний предоставим устанавливать пользователю. Из "выпавших" чисел x и y будем подсчитывать число случаев, когда: а) x + y > +10; б) x mod y = 0.
Это число случаев разделим на общее число бросаний и получим искомую вероятность (фактически мы получим частоту появления событий о чём речь шла выше).
Программы
Program Problem10a;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m : longint;
{-------------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{-------------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{-------------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random(6) + 1; y := random(6) + 1;
if (x + y >= 10) then m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Program Problem10b;
uses WinCrt;
var
p, e, pp : real;
x, y, i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random(6) + 1; y := random(6) + 1;
if x mod y = 0 then
m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
156. Какова вероятность, что при первом бросании выпадет не меньше 5 очков, а при втором - не меньше 4?
157. Какова вероятность, что хотя бы при одном из двух бросаний кубика выпадет не менее 5 очков?
158. Какова вероятность, что количество очков, выпавших при двух бросаниях, отличаются не более чем на 1?
159. (Случайные числа и точки: равномерное распределение). Найдите вероятность того, что сумма x + y, где x, y - случайные числа на отрезке [0; 1], больше данного числа a.
160. На отрезке [0; 1] случайно выбираются три числа. Какова вероятность того, что а) выбранное последним число наибольшее? б) числа идут в порядке возрастания?
161. На окружности случайно выбраны четыре точки A, B, C, D. Какова вероятность того, что отрезки AC и BD пересекаются?
162. а) В окружности проведен диаметр. На нём случайно выбирается точка и через нее проводится хорда, перпендикулярная диаметру. Какова вероятность, что длина хорды больше радиуса окружности?
б) На окружности случайно выбираются две точки. Какова вероятность, что длина соединяющей их хорды больше радиуса?
в) В круге случайно выбрана точка. Какова вероятность, что хорды с серединой в этой точке больше радиуса?
г) Решите аналогичные задачи про хорду длины r

Замечание. Задачи а), б), в) как бы три варианта одной и той же: проведем случайную прямую, пересекающую окружность: какова вероятность, что длина высекаемой хорды больше радиуса? Но ответ в них разный (парадокс Бертрана)!
163. На окружности случайно выбраны три точки.
Какова вероятность, что у треугольника с вершинами в этих точках: а) есть угол больше 30 градусов? б) все углы больше 30 градусов? в) все углы меньше 120 градусов?
164. На отрезке случайно выбраны две точки. Какова вероятность, что из отрезков, на которые он разбит, можно составить треугольник?
165. Плоскость разбита сеткой прямых на а) квадраты; б) правильные треугольники со стороной 1. Какова вероятность, что монета диаметра 1, случайно брошенная на плоскость, закроет одну из вершин сетки?
166. Найдите вероятность того, что а) выпуклый n-угольник с вершинами в случайных точках окружности содержит ее центр?
б) Докажите, что вероятность того, что n случайно выбранных точек на сфере лежат на одной полусфере (по одну сторону от некоторого большого круга) равна (n2 - n + 2)/2n.
Ответы
К заданию 2
Так как общее число карточек равно 7, то их можно упорядочить 7! способами. Поскольку обе буквы Т и обе буквы Р можно менять местами, не изменяя слова, то слово ТРАКТОР получится
2!.2! раза. Искомая вероятность равна:

Иначе тот же результат можно было бы получить, заметив, что в результате извлечения карточек мы получаем перестановку с повторениями состава (2, 2, 1, 1, 1), причем все такие перестановки имеют одну и ту же вероятность. Так как число перестановок равно P(2, 2, 1, 1, 1), то вероятность каждой из перестановок
равна

Program problem2;
uses WinCrt;
var
p : real;
k1, k : integer;
{----------------------------------------------------------------------------------------}
Procedure fakt(n : integer; var f : integer);
var
i : integer;
begin
f := 1;
if n = 0 then f := 1
else for i := 1 to n do
f := f*i
end;
{----------------------------------------------------------------------------------------}
begin
fakt(7, k); fakt(2, k1);
p := (k1*k1)/k;
writeln('Вероятность получ. слова "трактор" равна ', p:10:8)
end.
К заданию 3
Приведем лишь математическое решение задачи. Последующее составление программы достаточно простое.
Вычислить: P4(3) и P6(4).
По формуле Бернулли


Далее необходимо сравнить полученные результаты и сделать вывод.
К заданию 4 (пример 1)
{ Биномиальный закон распределения вероятностей }
Program Problem4_1;
uses WinCrt;
var
p, pp : real;
n, i : integer;
{----------------------------------------------------------------------------------------}
{ Процедура возведения в степень }
Procedure
Extent(a : real; n : integer; var e : real);
var
i : integer;
begin
e := 1;
if n = 0 then e := 1
else for i := 1 to n do e := e*a
end;
{----------------------------------------------------------------------------------------}
{ Рекуррентная процедура вычисления биномиального закона }
{ распределения }
Procedure Recurro_binomial(n, k : integer; p : real; var pp : real);
var
i : integer;
begin
Extent(1 - p, n, pp);
for i := 1 to k do pp := (pp*(n - i + 1)*p)/(i*(1 - p))
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите общее число рождений '); readln(n);
write('Введите вероятность рождения мальчика '); readln(p);
writeln('Биномиальный закон распределения вероятностей');
writeln;
for i := 0 to n do
write(i:6, ' '); writeln; writeln;
for i := 0 to n do
begin
Recurro_binomial(n, i, p, pp); write(pp:1:4, ' ')
end;
writeln; writeln;
Recurro_binomial(10, 6, p, pp);
writeln('Вероятность того, что из 10 наугад выбранных');
writeln('рождений будет 6 мальчиков, равна ', pp:1:6)
end.
К заданию 7
{ Распределение Пуассона }
Program Problem7;
uses WinCrt;
var
n, m : longint;
p, a : real;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления вероятности распределения Пуассона }
Function PS(m : integer; a : real) : real;
var
i : integer;
pp : real;
begin
pp := exp(-a);
if m = 0 then pp := exp(-a)
else for i := 1 to m do pp := pp*a/i;
PS := pp
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите общее число изделий '); readln(n);
write('Введите вероятность изделия быть бракованным ');
readln(p);
writeln('Введите число бракованных изделий, вероятность ');
write('появления которых Вы находите '); readln(m);
a := n*p;
writeln('Вероятность ', m, ' бракованных изделий в ');
writeln('партии из ',n, ' изделий равна ', PS(m, a):1:6)
end.
К заданию 9
{ Применение интегральной формулы Муавра-Лапласа }
Program Problem1;
uses WinCrt;
var
n, m1, m2 : longint;
p, PP : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if
x >= 5
then
FF := 1
else if x <= -5
then
FF := -1 else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисл. вероятн. наст. событ. из промеж. [m1; m2] }
Procedure
Interval(n, m1, m2 : longint; p : real; var PP : real);
var
x1, x2 : real;
begin
x1 := (m1 - n*p)/sqrt(n*p*(1 - p));
x2 := (m2 - n*p)/sqrt(n*p*(1 - p));
PP := (FF(x2) - FF(x1))/2
end;
{----------------------------------------------------------------------------------------}
{ Основная программа. Число бракованных изделий из промежутка }
begin
write('Введите общее число изделий '); readln(n);
write('Введите вероятность наступление одного события ');
readln(p);
write('Введите левую границу промежутка '); readln(m1);
write('Введите правую границу промежутка '); readln(m2);
Interval(n, m1, m2, p, PP);
writeln('Вероятность того, что число бракованных изделий');
write('находится в промежутке [',m1, '; ', m2, '] равна ');
writeln(PP:1:8)
end.
{ Применение интегральной формулы Муавра-Лапласа }
Program Problem2;
uses WinCrt;
var
n, m1, m2 : longint;
p, q, PP : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if
x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисл. вероятн. наст. событ. из промеж. [m1; m2] }
Procedure
Interval(n, m1, m2 : longint; p : real; var PP : real);
var
x1, x2 : real;
begin
x1 := (m1 - n*p)/sqrt(n*p*(1 - p));
x2 := (m2 - n*p)/sqrt(n*p*(1 - p));
PP := (FF(x2) - FF(x1))/2
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите общее число изделий '); readln(n);
write('Введите вероятность брака в одном изделии '); readln(q);
write('Введите левую границу промежутка '); readln(m1);
write('Введите правую границу промежутка '); readln(m2);
p := 1 - q;
Interval(n, m1, m2, p, PP);
writeln('Вероятность того, что число пригодных изделий');
write('находится в промежутке [',m1, '; ', m2, '] равна ');
writeln(PP:1:8)
end.
К заданию 10
{ Процедура нахождения числа испытаний n, чтобы обеспечить }
{ заданную вероятность отклонения частоты от np }
Procedure Number(p, e, PP : real; var n : longint);
var
x : real;
begin
x := 0;
repeat
x := x + 0.01
until
FF(x) >= PP;
n := round(e/(x*sqrt(p*(1 - p))) + 0.5);
n := sqr(n)
end;
{ Применение интегральной формулы Муавра-Лапласа }
Program Task10;
uses WinCrt;
var
n : longint;
e, q, PP : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if
x >= 5
then
FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура нахождения числа испытаний n }
Procedure Number(p, e, PP : real; var n : longint);
var
x : real;
begin
x := 0;
repeat
x := x + 0.01
until FF(x) >= PP;
n := round(e/(x*sqrt(p*(1 - p))) + 0.5);
n := sqr(n)
end;
{----------------------------------------------------------------------------------------}
begin
write(' Введите вероятность отклонения клемм от принято');
write('го стандарта '); readln(q);
write('Введите число стандартных клемм отличающихся ');
write('от np (по модулю) '); readln(e);
write('Укажите вероятность этого отклонения '); readln(PP);
Number(q, e, PP, n);
writeln('Искомое число взятых наудачу клемм равно ', n)
end.
К заданию 11
{ Процедура определение границы отклонения (ReIection) частости}
{ от заданной вероятности наступления одного события }
Procedure ReIection(n : longint; p, PP, eps : real; var e : real);
var
x : real;
begin
x := 0;
repeat
x := x + eps
until
FF(x) >= PP;
e := x*sqrt(p*(1 - p)/n)
end;
{ Применение интегральной формулы Муавра-Лапласа }
Program Task3;
uses WinCrt;
var
n : longint;
e, eps, p, pp : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if
x >= 5
then
FF := 1
else if x <= -5
then
FF := -1
else
begin
u := x;
n := 0;
I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура определение границы отклонения (ReIection) частости}
{ от заданной вероятности наступления одного события }
Procedure ReIection(n : longint; p, PP, eps : real; var e : real);
var
x : real;
begin
x := 0;
repeat
x := x + eps
until
FF(x) >= PP;
e := x*sqrt(p*(1 - p)/n)
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите вероятность события в каждом испытании '); readln(p);
write(' Введите общее число произведенных испытаний '); readln(n);
write('Укажите гарантированную вероятность '); readln(PP);
write('Укажите точность вычисления искомой величины '); readln(eps);
ReIection(n, p, PP, eps, e);
writeln('Искомая граница отклонения частости от вероят-');
write('ности будет находиться в промежутке ');
writeln('[', p-e:1:4, '; ', p+e:1:4, ']')
end.
К заданию 12
{ Применение интегральной формулы Муавра-Лапласа }
Program Problem12;
uses WinCrt;
var
n : longint;
e, p, PP : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура нахождения числа испытаний n, чтобы обеспечить }
{ заданную вероятность отклонения частности от заданного числа }
Procedure
Number3(p, e, PP : real; var n : longint);
var
x : real;
begin
x := 0;
repeat
x := x + 0.01
until FF(x) >= PP;
n := round((x*sqrt(p*(1 - p))/e) + 0.5);
n := sqr(n)
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write(' Введите постоянную для каждого испытания ');
write('вероятность '); readln(p);
writeln('Введите число, от которого по абсолютной ');
write('величине должна отличаться частость '); readln(e);
write('Укажите гарантированную вероятность '); readln(PP);
writeln;
Number3(p, e, PP, n);
writeln('Число испытаний должно быть больше или равно ', n)
end.
К
заданию 15
Program Normal1;
uses WinCrt;
var
PP, x, l, c : real;
{-----------------------------------------------------------------------------------------}
{ Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура нахождения аргумента x }
Procedure Argument(PP : real; var
x : real);
begin
x := 0;
repeat
x := x + 0.0001
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
write(' Введите среднее квадратическое отклонение '); readln(c);
write('Введите вероятность попадания в интервал, симметричн. M(X) ');
readln(PP);
Argument(PP, x);
l := 2*c*x;
writeln('Длина искомого интервала равна ', L:4:6)
end.
Ответ к задаче 2 задания
Указание
По формуле (6) находим

Ответ
0.06.
Program Exercise_Normal2;
uses WinCrt;
var
PP, x, a, d, e, c : real;
{----------------------------------------------------------------------------------------}
{ Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until
abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура нахождения аргумента x }
Procedure Argument(PP : real; var
x : real);
begin
x := 0;
repeat
x := x + 0.0001
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите среднее значение ');
writeln('нормально распределенной случайной величины a = M(X) ');
write('т.е. средний диаметр детали '); readln(a);
write('Введите дисперсию '); readln(d);
writeln('Введите гарантированную вероятность');
write(' отклонения детали от среднего размера '); readln(PP);
Argument(PP, x);
c := sqrt(d);
e := c*x;
writeln('Максимальное отклонение диаметра от среднего равно ', e:2:6)
end.
Ответ к задаче 3 задания
а) 0.9986; б) 0.7823.
Program Exercise_Normal13a;
uses WinCrt;
var
e, c, d, pp, p1, sum : real;
n, m, i : integer;
{----------------------------------------------------------------------------------------}
{ Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура возведения в степень }
Procedure Extent(a : real; n : integer; var e : real);
var
i : integer;
begin
e := 1;
if n = 0 then e := 1 else for i := 1 to n do
e := e*a
end;
{--------------------------------------------------------------------------------------}
{ Рекуррентная процедура вычисления вероятности }
{ биномиального закона распределения }
Procedure Recurro_binomial(n, m : integer; p : real; var p1 : real);
var
i : integer;
begin
Extent(1 - p, n, p1);
for
i := 1 to m do p1 := (p1*(n - i + 1)*p)/(i*(1 - p))
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите дисперсию '); readln(d); c := sqrt(d);
write(' Введите отклонение детали от заданного размера '); readln(e);
write('Введите число измерений '); readln(n);
write('Введите допускаемое число появления ощибок '); readln(m);
pp := 1 - FF(e/c);
sum := 0;
for i := 0 to m do
begin
Recurro_binomial(n, i, pp, p1);
sum := sum + p1
end;
writeln('Вероятность брака равна ', sum:1:6)
end.
К
заданию 16
Program Task16_1;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m, a, b : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1; x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите длину отрезка - a = '); readln(a);
write('Введите расстояние b от точки A '); readln(b);
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random*a; y := random*a;
if (x <= b) and (y <= b) then m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Program Task16_2;
uses WinCrt;
var
x, y, p, a, q, k1, h, e, pp : real;
i, n, k, m : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1; x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите длину стороны BC '); readln(a);
write('Введите высоту трапеции '); readln(h);
write('Введите величину угла BAE < Pi/2 в рад '); readln(q);
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
k := 0; m := 0; k1 := sin(q)/cos(q);
for i := 1 to n do
begin
x := random*(2*h/k1 + a); y := random*h;
if (y < k1*x) and (y < -k1*x + k1*(2*h/k1 + a)) then k := k + 1;
if ((x < h/k1) and (y < k1*x)) or
((x > a + h/k1) and
(y < -k1*x + k1*(2*h/k1 + a))) then m := m + 1
end;
p := m/k;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
К заданию 17
Пусть событие E - точка оказалась внутри куба с ребром, равным 3 см. Будем считать, что исходы испытания распределены равномерно. Тогда вероятность наступления события E пропорциональна мере этого куба и равна:

V2 - объем параллелепипеда.
Program Task17;
uses WinCrt;
var
x, y, z, p, e, pp : real;
i, n, s : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
s := 0;
for i := 1 to n do
begin
x := random*4; y := random*6; z := random*10;
if (x < 3) and (y < 3) and (z < 3) then s := s + 1
end;
p := s/n;
writeln('Вероятность появление точки внутри куба ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
К
заданию 18
Program Task18_1;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random*12;
y := random*12;
if (y > x - 3) and (y < x + 3) then m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Program Task18_2;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random*20;
y := random*20;
if (y > x - 5) and (y < x + 5) and
(y > x - 2) and (y < x + 2)
then m := m + 1
end;
p := (2*m)/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
К
заданию 19
Program Task19;
uses WinCrt;
var
p, x, y, z, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random; y := random; z := random;
if ((x < 1/3) and (y > 1/3) and (y < 2/3) and (z > 2/3)) or
((y < 1/3) and (x > 1/3) and (x < 2/3) and (z > 2/3)) or
((y < 1/3) and (z > 1/3) and (z < 2/3) and (x > 2/3)) or
((z < 1/3) and (x > 1/3) and (x < 2/3) and (y > 2/3)) or
((z < 1/3) and (y > 1/3) and (y < 2/3) and (x > 2/3)) or
((x < 1/3) and (z > 1/3) and (z < 2/3) and (y > 2/3))
then m := m + 1
end;
p := m/n;
writeln(' Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Досрочное прерывание цикла Метка Оператор безусловного перехода goto
Итак, если в числе появляется цифра 2, надо прервать цикл, т. е. нарушить естественный ход выполнения программы, выдать соответствующее сообщение и закончить программу. Такой безоговорочный переход может выполнить оператор goto, который и называется оператором безусловного перехода.
Оператор перехода указывает, что дальше программа должна выполняться, начиная с оператора, помеченного меткой, которая записана в этом операторе перехода.
Оператор перехода имеет вид: goto <метка>. Здесь goto - зарезервированное слово (перейти на ... [метку]).
Метка
в Турбо Паскале - это произвольный идентификатор, позволяющий именовать (помечать) некоторый оператор программы и таким образом ссылаться на него. Допускается в качестве меток (в том числе) использовать целые числа без знака (это сделано с целью совместимости Турбо Паскаля со стандартным языком Паскаль).
Например:
goto 2341, goto 23, goto
1, goto bl1, goto mnk3, goto n56.
Любая метка должна быть описана в разделе описания меток, который обычно располагается в программе до начала раздела операторов:
label
<список меток>.
Например: label
2341; label 1, 2; label bl1, 18, mnk.
В программе метка записывается перед оператором, на который осуществляется переход. Метка отделяется от оператора двоеточием. Между меткой и оператором можно включать один или несколько пробелов, например:
1: writeln('Число не содержит цифру 2');
Оператор можно помечать несколькими метками, которые в этом случае отделяются друг от друга двоеточием.
1: 25: a := b div
10;
Теперь составим программу решения предыдущей задачи с использованием меток и оператора перехода.
Ниже приведена эта программа.
Program
Problem4a; { Входит ли цифра 2 в запись числа }
uses WinCrt;
label 1, 2;
var
n, p : integer;
begin
write('Введите целое число '); readln(n);
while n <> 0 do
begin
p := n mod 10;
if p = 2 then goto 1 else n := n div
10
end;
writeln('Цифра 2 не входит в запись этого числа');
goto
2;
1: writeln('Цифра 2 входит в запись этого числа');
2: end.
Внимательно разберитесь в ее работе. Постарайтесь ответить на следующие вопросы.
1) Зачем в программе две метки? Для чего служит каждая из них?
2) Почему в программу введен второй оператор перехода goto 2?
3) Как будет выполняться программа, если этот оператор исключить из нее?
Двумерные случайные величины
Вначале введем понятие независимости случайных величин.
Дискретные случайные величины X и Y называются независимыми, если независимы при любых i и I события X = xi и Y = yI (i = 1, 2, ..., n; I = 1, 2, ..., m).
Понятие независимости случайных величин распространяется на любое конечное число случайных величин.
Случайные величины, которые рассматривались ранее, называются еще одномерными. В теории вероятностей рассматриваются еще, так называемые двумерные, трехмерные и вообще многомерные случайные величины.
Определение. Случайная величина называется двумерной, если все значения ее имеют вид (xi, yI), причем 1




Событие, заключающееся в том, что двумерная величина примет значение (xi,yi), означает произведение двух событий:
1) случайная величина X примет xi;
2) случайная величина Y примет значение yi. Вероятность этого события обозначим piI: piI = = P(X = xi; Y = yi). Совокупность всех пар значений (xi, yi) и соответствующих им вероятностей piI составляет закон распределения двумерной случайной величины.
Обозначим через P (Y=yi) условную вероятность того, что X=xi случайная величина Y примет значение yi относительно события, состоящего в том, что случайная величина X приняла значение xi. По определению эту вероятность считаем равной:

Пример 1. Известны результаты стрельб для 2-х стрелков при 3-ч выстрелах: X - число попаданий первого стрелка, Y - число попаданий второго стрелка.
| xi | 1 | 2 | 3 | yi | 1 | 2 | 3 | ||||||||
| pi | 0.3 | 0.2 | 0.5 | pi | 0.1 | 0.6 | 0.3 |
Найти среднее число попаданий каждого стрелка и среднее квадратическое отклонение этих случайных величин.
Решение
По формуле для вычисления математического ожидания

По формуле

Сравнив их, выясним который из стрелков получает лучший результат при стрельбе.
Программа
Program
Two_dimensional_aleatory_variables1;
uses WinCrt;
Const
k = 10;
Type
t = array[1..k] of real;
var
Px , Py : t;
MX, MY, DX, DY : real;
n, m, i : integer;
begin
write('Введите число выстрелов первого стрелка '); readln(n);
write('Введите число выстрелов второго стрелка '); readln(m);
writeln;
writeln('Вводите вероятности попаданий первого стрелка');
MX := 0;
for i := 1 to n do
begin
write('Вероятность попадания при ', i, '-ом выстреле ');
readln(px[i]);
MX := MX + i*px[i]
end;
writeln('Среднее число попаданий первого стрелка ', MX:2:4);
writeln;
writeln('Вводите вероятности попаданий второго стрелка');
MY := 0;
for i := 1 to m do
begin
write('Вероятность попадания при ', i, '-ом выстреле ');
readln(py[i]);
MY := MY + i*py[i]
end;
writeln('Среднее число попаданий второго стрелка ', MY:2:4);
writeln;
DX := 0;
for i := 1 to n do DX := DX + sqr(i - MX)*px[i];
DY := 0;
for i := 1 to m do DY := DY + sqr(i - MY)*py[i];
if sqrt(DX) < sqrt(DY)
then writeln('Первый стрелок стреляет лучше')
else
if sqrt(DX) > sqrt(DY)
then writeln('Второй стрелок стреляет лучше')
else writeln('Стрелки стреляют с одинаковой точностью')
end.
Пример 2. По данным задачи 1 найти ряд распределения случайной величины Z, равной а) X + Y; б) 5X + 3Y.
Определить в каждом случае математическое ожидание и дисперсию.
Решение
а) Для нахождения значений Z можно воспользоваться матрицей сумм значений X и Y.
|
X\Y |
1 |
2 |
3 |
|
1 |
(1 + 1) |
(1 + 2) |
(1 + 3) |
|
2 |
(2 + 1) |
(2 + 2) |
(2 + 3) |
|
3 |
(3 + 1) |
(3 + 2) |
(3 + 3) |
Procedure Sum(n, m : integer; x, y : t; var zz : t);
var
i, I, k : integer;
begin
k := 0;
for i := 1 to n do
for I := 1 to m do
begin
k := k + 1;
zz[k] := x[i] + y[I]
end
end;
В результате получаются значения Z, среди которых будут повторяющиеся (2, 3, 3, 3, 4, 5, 4, 5, 6).
Необходимо выбрать только различные значения суммы Z = X + Y.
Это можно выполнить с помощью процедуры, которая детально рассматривается в главе "Задачи с массивами чисел".
{ Процедура отбора различных элементов в массиве Z }
Procedure Different(n, m : integer; var z : t; var k : integer);
label 1;
var
i, I : integer;
begin
k := 0;
for i := 1 to n*m do
begin
for I := 1 to k do
if z[i] = z[I] then goto 1;
k := k + 1;
z[k] := z[i];
1: end
end;
Получим, для нашего примера, что Z может принимать значения 2, 3, 4, 5, 6. Определим вероятности, учитывая, что X и Y независимы.
P(Z = 2) = P(X = 1)P(Y = 1);
P(Z = 3) = P(X = 1)P(Y = 2) + P(X = 2)P(Y = 1);
P(Z = 4) = P(X = 1)P(Y = 3) + P(X = 2)P(Y = 2) + P(X = 3)P(Y = 1);
P(Z = 5) = P(X = 2)P(Y = 3) + P(X = 3)P(Y = 2);
P(Z = 6) = P(X = 3)P(Y = 3);
В результате получаем ряд распределения вероятностей.
Используя свойства математического ожидания и дисперсии и результаты примера 1, находим M(Z) = M(X) + M(Y); D(Z) = D(X) + D(Y).
Программа
Program Problem2;
uses WinCrt;
const
p = 20;
type
t = array[1..p] of integer;
tt = array[1..p] of real;
var
x, y, z : t;
px, py, pz : tt;
n, m, k, n1, i : integer;
MX, MY, MZ, DX, DY, DZ : real;
{-----------------------------------------------------------------------------------------------}
{ Процедура суммирования значений X и Y и получение Z }
Procedure Sum(n, m : integer; x, y : t; var z : t);
var
i, I, k : integer;
begin
k := 0;
for i := 1 to n do
for I := 1 to m do
begin
k := k + 1;
z[k] := x[i] + y[I]
end
end;
{-----------------------------------------------------------------------------------------------}
{ Процедура отбора различных элементов в массиве Z }
Procedure Different(n, m : integer; var z : t; var k : integer);
label 1;
var
i, I : integer;
begin
k := 0;
for i := 1 to n*m do
begin
for I := 1 to k do
if z[i] = z[I] then goto 1;
k := k + 1;
z[k] := z[i];
1: end
end;
{-----------------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите число стрелков '); readln(n1);
write(' Введите число выстрелов, сделанных первым стрелком '); readln(n);
write('Введите число выстрелов, сделанных вторым стрелком '); readln(m);
writeln('Вводите вероятности попаданий первого стрелка');
MX := 0;
for i := 1 to n do
begin
write('Вероятность попадания при ', i, '-ом выстреле ');
readln(px[i]);
MX := MX + i*px[i]
end;
writeln(' Среднее число попаданий первого стрелка ', MX:2:4);
writeln;
writeln('Вводите вероятности попаданий второго стрелка');
MY := 0;
for i := 1 to m do
begin
write('Вероятность попадания при ', i, '-ом выстреле ');
readln(py[i]);
MY := MY + i*py[i]
end;
writeln('Среднее число попаданий второго стрелка ', MY:2:4);
writeln;
DX := 0;
for i := 1 to n do DX := DX + sqr(i - MX)*px[i];
DY := 0;
for i := 1 to m do DY := DY + sqr(i - MY)*py[i];
MZ := MX + MY; DZ := DX + DY;
writeln('Искомый ряд распределения вероятностей');
for i := 1 to
n do
begin
x[i] := i;
y[i] := i
end;
Sum(n, m , x, y, z);
Different(n, m, z, k);
for i := 1 to k do write(z[i]:4, ' '); writeln;
pz[1] := px[1]*py[1];
pz[2] := px[1]*py[2] + px[2]*py[1];
pz[3] := px[1]*py[3] + px[2]*py[2] + px[3]*py[1];
pz[4] := px[2]*py[3] + px[3]*py[2];
pz[5] := px[3]*py[3];
for i := 1 to k do write(pz[i]:2:2, ' '); writeln;
writeln('Математическое ожидание равно ', MZ:2:4);
writeln('Дисперсия равна ', DZ:2:4)
end.
Форматированный вывод информации
Если вы выполните программу, то столкнетесь с неприятным явлением - результат, т.е. числовые значения корней, будут выдаваться на экран в экспоненциальной форме.
Так, после ввода значений коэффициентов: 2 3 -10, на экран будет выдан результат:
Уравнение имеет два различных корня
x1 = -3.1084952830E+00 x2 = 1.6084952830E+00
Во-первых, такой результат неудобно читать и запоминать, во-вторых, нам не всегда нужна высокая точность вычисления и, в-третьих, даже целые значения корней будут выдаваться тоже в экспоненциальной форме, что уже совсем неудобно.
Чтобы избежать всех этих неприятностей, можно использовать форматированный вывод информации.
В Турбо-Паскале предусмотрен вывод данных с форматами. В общем случае формат имеет следующий вид:
r:f1:f2
Здесь r - имя переменной, значение которой выводится (в данном случае - x1 или x2), формат f1 указывает, сколько позиций нужно для всего числа, включая знак числа, целую часть, точку и дробную часть числа; f2 - число позиций дробной части числа (после точки).
Если формат указан, то значение переменной r выводится в виде константы с фиксированной запятой, например: 12.35, .123. Если параметры f1 и f2 опущены, то вещественная переменная выводится в виде константы с плавающей запятой, например: 2.534E03, 5.67E-12 и т.п. В этом случае значения f1 и f2 устанавливается по умолчанию.
Надо вообще заметить, что вещественное число в формате с фиксированной точкой печатается так:
несколько пробелов; знак минус (-) или пробел; последовательность цифр (целая часть); точка; последовательность цифр (дробная часть).
Рассмотрим несколько примеров форматированного вывода результатов для вещественных переменных.
Пример. Пусть переменная r получает значение частного от деления вещественных переменных a на b.
Составим небольшую программу и выполним ее несколько раз, устанавливая различные значения для форматированного вывода результата.
Program Problem;
uses WinCrt;
var
a, b, r : real;
begin
write('Введите значение переменной a '); readln(a);
write('Введите значение переменной b '); readln(b);
r := a/b;
writeln('Результат равен ', r)
end.
При первом выполнении программы не устанавливайте параметров для форматированного вывода. Вы получите результат в форме с плавающей запятой. При следующем выполнении для a введите значение 1, для b 3, а для вывода результата установите следующий формат: r:6:2; затем, r:1:5; r:0:4 и т.п.
Форматированный вывод возможен и для переменных целого типа, но в этом случае нужен только один параметр:
r:f1
Если значение формата f1 больше, чем необходимое число позиций для записи числа, то перед числом добавляется соответствующее число пробелов. Если значение f1 меньше, оно автоматически увеличивается до числа позиций, необходимого для вывода числа.
Изменим в программе две строки вывода информации:
writeln('Уравнение имеет один корень ', -b/(2*a):6:3) и
writeln('x1 = ', x1:6:3, ' x2 = ', x2:6:3)
Теперь понятно, что для выводимых результатов отведено 6 позиций, а для дробной части - 3 позиции, т.е. до тысячных долей (думается этого достаточно для школьных задач).
Формула Бернулли
Схема повторных независимых испытаний.
Рассмотрим опыт, который состоит в том, что испытания повторяются многократно, причем выполнены следующие условия:
1) все испытания независимы друг от друга, т.е. вероятность появления события А в каждом из них не зависит от того, произошло или не произошло рассматриваемое событие в других опытах;
2) каждое испытание имеет только два исхода:
а) событие А произошло; б) событие А не произошло;
3) вероятность появления события А в каждом испытании постоянна и равна p, а следовательно, вероятность не появления события А равна q = 1 - p.
Так как в каждом из n проводимых испытаний событие А может произойти или не произойти, то полученная схема повторных независимых испытаний содержит 2n точек.
Примерами повторных независимых испытаний с двумя исходами могут служить:
1) многократное подбрасывание монеты;
2) стрельба по цели n раз одиночными выстрелами, если нас интересует только попадание или промах;
3) массовый контроль деталей, при котором требуется только установить, какой является деталь, стандартной или нестандартной.
Некоторые задачи, описываемые по такой схеме, можно решить, используя формулу для непосредственного подсчета вероятностей или теореме о вероятности суммы и вероятности произведения событий. Однако, проще воспользоваться формулой Бернулли. Пусть необходимо вычислить вероятность появления события А ровно m раз при проведении n повторных независимых испытаний.
Вероятность появления события А равна p, а вероятность не появления события А равна q, тогда вероятность появления события А ровно m раз при проведении n независимых испытаний равна:

Эту формулу называют формулой Бернулли.
Пример 4. Известно, что при каждом взвешивании равновозможна как положительная, так и отрицательная ошибка. Какова вероятность того, что при пяти взвешиваниях получатся три положительные ошибки?
Математическое решение задачи
Проводится 5 независимых испытаний с двумя исходами, причем в каждом испытании p = q = 0,5.
Тогда по формуле Бернулли вероятность появления трех положительных ошибок равна:

Алгоритм
составления программы
Надо использовать не только процедуру вычисления числа сочетаний из n элементов по m, но и процедуру вычисления степени заданного вещественного числа a. Эта процедура нам знакома из предыдущего занятия.
Программа
Program Problem4;
uses WinCrt;
var
s1 : longint;
p, st, st1 : real;
{----------------------------------------------------------------------------------------}
Procedure combination(n, k : integer; var s : longint);
var
i : longint;
begin
s := 1;
if k = 0 then s := 1
else for i := 1 to n - k do s := s*(k + i) div i
end;
{----------------------------------------------------------------------------------------}
Procedure extent(a : real; n : integer; var q : real);
var
i : integer;
begin
q := 1;
for i := 1 to n do q := a*q
end;
{----------------------------------------------------------------------------------------}
begin
combination(5, 3, s1);
extent(0.5, 3, st);
extent(0.5, 2, st1);
p := s1*st*st1;
writeln('Искомая вероятность равна ', p:6:4)
end.
Формы записи вещественных чисел
В математике На Паскале
1. Естественная форма записи
135; 89245; -2,356; 0,28; 135; 89245; -2.356; 0.28
Как видите, отличие заключается в том, что вместо запятой используется точка.
2. Экспоненциальная форма записи или форма записи с плавающей запятой
3,7


При такой записи, множитель, стоящий перед степенью с основанием 10 называется мантиссой, а показатель степени десятки - порядком числа.
В наших примерах: 3.7 и 1.67 - мантиссы, а 5 и -12 - порядки чисел.
Мантисса может иметь 11...12 значащих цифр, а порядок от -39 до 38. (Это в Турбо Паскале версии 7.0 и Barland Pascal.)
Функции
Язык программирования Паскаль допускает введение в программу функции, определяемой пользователем. Она помещается в разделе описаний основной программы.
Запись функции начинается так:
Function
<имя> (<список формальных параметр.>) : <тип рез.>
var
<описание переменных, участвующих в работе функции>
Дальнейшее построение такое же, как и во всех других программах на языке Паскаль.
begin
<операторы>
<имя> := <результат>
end;
Обязательной
является команда присваивания имени функции результата, полученного в итоге ее работы. Функция может быть использована несколько раз в программе.
Для ее вызова достаточно указать имя функции и задать значение формальных параметров: <имя> (<значение параметров>).
Например: s(2, 3) или s(n, a). Параметры и переменные функции могут иметь те же имена, что и переменные в основной программе.
Снова обратимся к наиболее типичным примерам, создаваемых функций. Как вы смогли уже убедиться, их конструкция мало чем отличается от процедур, да и существует возможность обратных преобразований функций в процедуру и процедур в функции.
Известный ряд чисел Фибоначчи имеет вид:
1, 1, 2, 3, 5, 8, 13, 21, 34, ...
Каждый член этой последовательности, начиная с третьего, равен сумме двух предыдущих членов.
Если первый член последовательности обозначить f1, второй -



Пользуясь такой зависимостью, можно получить все члены последовательности чисел Фибоначчи.
Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной (от латинского слова recurro - возвращаться).
Зная зависимость между последующим и предыдущими членами, легко создать рекурсивную функцию, позволяющую найти n-е число ряда Фибоначчи:
Function fib(n : integer) : longint;
begin
if (n = 1) or (n = 2) then fib := 1
else fib := fib(n - 1) + fib(n - 2)
end;
Здесь, мы одновременно проследим и построение функции и рекурсии.
В заголовке указывается зарезервированное слово Function, далее пишется по фантазии пользователя ее имя, удовлетворяющее всем требованиям, предъявляемым к идентификаторам.
В скобках описываются, как и в процедурах, входные параметры, заметьте, в функции есть только входные параметры, в качестве выходного значения используется сама функция, поэтому обязательно указывается ее тип.
И вот теперь ее имя fib может быть использовано в программе, наряду со встроенными функциями, в различных операторах и арифметических вычислениях.
Построение самой функции начинается, как и построение любой другой программы, но обязательно надо присваивать конечное значение самой функции: fib.
Function fib(n : integer) : longint;
var
f, f1, f2, i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1; f1 := f;
f := f1 + f2;
end;
fib := f
end;
Конечно, удобно составлять программу, когда все члены ряда вычисляются по одному правилу, но в ряде Фибоначчи выпадают из общего правила два первых члена. Если мы хотим вычислить и их по тому же правилу, тогда следует в функции fib искусственно продолжить ряд влево, пополнив его двумя фиктивными членами: f(-1) = 1 и f(0) = 0. Тогда ряд примет следующий вид:
1 0 - фиктивные члены ряда
1 1 2 3 5 ... - подлинные члены ряда.
При наличии этих двух фиктивных членов все подлинные члены ряда вычисляются по тем же правилам.
Работу этой функции понять несложно, поэтому мы не будем останавливаться на детальном разборе ее работы.
Можно составить функцию для вычисления чисел Фибоначчи используя рекурсию, тогда она будет выглядеть более компактной:
Function fib(n : integer) : integer;
begin
if (n = 1) or (n = 2) then fib := 1
else fib := fib(n - 1) + fib(n - 2)
end;
Однако, несмотря на внешнюю изысканность, эта функция крайне неэффективна.
Давайте детально проследим за ходом ее работы.
Когда n = 1 или n = 2, получаем значение функции, выполнив функцию один (первый) раз.
Когда n = 3, выполняется вторая (else) ветвь условного оператора и значение функции находится из выражения fib(2) + fib(1).
Для того, чтобы вычислить значение выражения, следует еще два раза (рекурсивно) обратиться к функции fib.
Когда n = 4, функция будет выполняться пять раз, а когда n = 5 - девять раз.

fib(3) fib(2) fib(4) fib(3)
fib(2) fib(1) fib(3) fib(2) fib(2) fib(1)
fib(2) fib(1)
Таким образом, при возрастании значения параметра функции очень быстро возрастает и число обращений к функции, а тем самым увеличивается время вычисления. Это происходит от того, что вторая рекурсивная ветвь условного оператора содержит сразу два рекурсивных вызова. Поэтому эта рекурсивная функция служит примером очень часто встречаемых неэффективных рекурсивных функций.
Часто, внешняя любезность рекурсии оборачивается большими неприятностями.
Приведем и другой способ вычисления членов ряда Фибоначчи с помощью с помощью функции, построенной итеративно. Для ее построения возможны два способа.
Пример 1
Первый способ
Function
Fib(n: integer):longint;
var
f1, f2, f : longint;
i : integer;
begin
f2 := 1; f := 1;
if (n = 1) or (n = 2) then f := 1
else
for i := 3 to
n do
begin
f1 := f2; f2 := f
f := f1 + f2;
end;
fib := f
end;
Второй способ
Function fib(n : integer) : integer;
var
f, f1, f2, i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1; f1 := f;
f := f1+f2;
end;
fib := f
end;
Полностью программа:
Program Problem1;
uses WinCrt;
var
i, n : integer;
{----------------------------------------------------------------------------------------}
Function fib(n : integer) : integer;
var
f, f1, f2, i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1; f1 := f;
f := f1 + f2;
end;
fib := f
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите значение n '); readln(n);
writeln('Числа Фибоначчи');
for i := 1 to n do write(fib(i), ' ');
writeln
end.
Пример 2.
Последовательность (an) задается так:




Решение
При построение членов последовательности нам придется находить сумму цифр числа. Поэтому есть смысл составить функцию, которая определяет сумму цифр числа. Эта функция может быть построена так:
Function
Sum(a : integer) : integer;
var
s : integer;
begin
s := 0;
repeat
s := s + a mod 10;
a := a div 10
until a = 0;
Sum := s
end;
Вторая функция - это функция, с помощью которой можно получить любой член последовательности:
Function Succ(n : integer) : integer;
var
a, i : integer;
begin
a := 7;
for i := 2 to n do
a := Sum(a*a) + 1;
Succ := a
end;
Полностью программа может быть построена так:
Program Succession; { succession - последовательность }
uses WinCrt;
var
a, i, n : integer;
{----------------------------------------------------------------------------------------}
Function Sum(a: integer): integer;
var
s: integer;
begin
s:=0;
repeat
s := s + a mod 10;
a := a div 10
until a = 0;
Sum := s
end;
{----------------------------------------------------------------------------------------}
Function Succ(n : integer): integer;
var
a, i : integer;
begin
a := 7;
for i := 2 to n do
a := Sum(a*a) + 1;
Succ := a
end;
{----------------------------------------------------------------------------------------}
begin
write(' Введите число членов последовательности ');
readln(n);
for i := 1 to n do write(Succ(i), ' ');
writeln
end.
Функция random и процедура randomize
Функция random генерирует случайное вещественное число из промежутка

Возникает естественный вопрос, а как выработать случайное вещественное число из произвольного промежутка [a; b]?
Для этого надо умножить случайное число из промежутка [0; 1], т.е. значение функции random, разность b - a и прибавить левую границу промежутка - a.
Случайное вещественное число из промежутка [a; b] получается от умножения значения функции random на разность b-a и прибавления к результату левой границы промежутка - числа a: random*(b - a) + a
Например, для получения случайного вещественного числа из промежутка

а для получения случайного вещественного числа из промежутка [0; 100] надо значение random умножить на 100: random*100.
Функция random(x), где x - целое число (тип: integer), выдает случайное целое число из промежутка [0; x). Значения функции random(x) имеют тип integer.
Например, значением функции random(6) является случайное целое число из промежутка [0; 6) или из [0; 5].
Как с помощью этой функции получить случайное целое число из промежутка [a; b], где a и b целые числа? Это можно сделать с помощью функции:

Например, случайное целое число из промежутка [15; 18] задается функцией:
random(4)+15.
Есть одна особенность в использовании функций случайных чисел или, как еще их называют, генераторов случайных чисел. При повторном обращении к ним, они могут повторять предыдущие значения. Чтобы избежать этого неприятного явления, перед их применением надо использовать процедуру инициализации этого генератора случайных чисел. Такая процедура есть. Ее имя randomize.
Процедура randomize инициализирует датчик случайных чисел random.
Итак, перед использованием в программе датчика псевдослучайных чисел random в программу надо включать процедуру randomize, которая инициализирует датчик случайных чисел.
Пример 1.
На стержне AB, длина которого равна 36 см, нанесена наудачу тонкая риска. Какова вероятность того, что эта риска окажется не далее a от конца A или не далее b от середины стержня: 1) a = 6 см, b = 2 см; 2) a = 12 см, b = 10 см?
Алгоритм
Числовую ось OX расположим так, что ее начало совпадает с левым концом отрезка - точкой A. Тогда нанесение риски на стержень будет означать случайный выбор значения X из промежутка [0; 36] и задаваться следующим равенством:
x := random*36.
Риска должна быть не далее a от начала отрезка, т. е. значения x должно удовлетворять неравенству (см. рис. 30):

Не далее b от середины отрезка означает, что

Надо подсчитать количество значений x, удовлетворяющих неравенствам:

Пусть их число равно m, а общее число "брошенных" на отрезок точек - n. Тогда искомая вероятность будет равна: p = m/n.
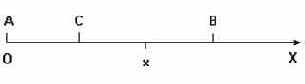
Рис. 30
Для определения точности вычисления вероятности, которая равна частости появления события (m/k), а отсюда и числа испытаний, можно воспользоваться способом, который уже применялся при изучении интегральной формулы Муавра-Лапласа.
В зависимости от гарантированной вероятности и точности вычисления можно установить необходимое число испытаний - n, а затем, по числу испытаний рассчитать вероятность.
Возможность применения формулы Муавра-Лапласа к решению геометрической задачи методом Монте-Карло дает следующие обстоятельства.
Испытания, т.е. "бросание" точек, независимы и равновозможны. Вероятность наступления события в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний может быть достаточно велико.
Таким образом, все условия для применения формулы Муавра-Лапласа выполнены. А теперь вспомним пример, в котором находится число испытаний в зависимости от заданной вероятности и точности вычисления.
Для этого можно использовать процедуры и функции из раздела "Интегральная формула Муавра-Лапласа" (в частности, в примере 6).
Вероятность некоторого события хотят установить статистически.
Для этого проводят некоторое количество испытаний, и частость появления события принимают за его вероятность. Сколько надо произвести испытаний, чтобы с вероятностью 0.97 можно гарантировать, что вероятность события в одном испытании будет отличаться от частости полученной из опыта, не более, чем на 0.01?
Одна из идей, которыми можно воспользоваться и реализовать программными средствами, состоит в том, чтобы непосредственным подбором числа n найти его искомое значение.
Для этого достаточно организовать цикл, завершающим условием которого является:


Чтобы найти x нужно воспользоваться соотношением: x := 2*e*sqrt(n).
В результате можно составить следующую процедуру:
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until
FF(x) >= PP
end;
Основываясь на этой процедуре составим программу.
{ Применение интегральной формулы Муавра-Лапласа }
Program Problem6;
uses WinCrt;
var
n : longint;
e, pp : real;
{-------------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{-------------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{-------------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления частости '); readln(e);
NumberExperiment(e, PP, n);
writeln('Число испытаний равно ', n );
writeln('С точностью до ', e:1:8)
end.
Используя процедуры из предыдущей программы, составим программу решения геометрической задачи. Надо сразу заметить, что точность вычисления будет невысокой. При увеличении точности даже с гарантированной вероятностью 0.97, не говоря уже о вероятности 0.99, резко возрастает число испытаний и программа становится трудоемкой для выполнения.
Программа
Program Problem1;
uses WinCrt;
var
x, a, b, p, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Интегральная функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите расстояние a от конца стержня '); readln(a);
write('Введите расстояние b от середины стержня '); readln(b);
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random*36;
if (x <= a) or (abs(18 - x) <= b) then m := m + 1;
end;
p := m/n;
writeln('Вероятн. появления риски в заданном месте ',p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Пример 2. На отрезке AB длины l независимо друг от друга выбираются наудачу две точки M и N. Какова вероятность того, что точка M окажется ближе к точке A, чем точка N?
Алгоритм
Пусть |AM| = x, |AN| = y. Рассматриваемому событию будут благоприятствовать лишь те точки, которые удовлетворяют условию y>x. Множество всех возможных исходов испытания можно изобразить в виде квадрата, сторона которого равна l (см. рис. 31).
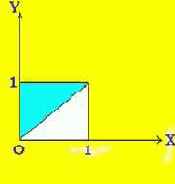
Рис. 31
Множество исходов испытания, благоприятствующих рассматриваемому событию, геометрически изображается точками заштрихованного треугольника.
Координаты всех точек этого треугольника удовлетворяют неравенству: y>x.
Программа
Program Problem2;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m : longint;
{--------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer; u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random;
y := random;
if y > x then m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Функциональные ряды
Функциональным рядом
называется выражение


Примеры
функциональных рядов.



Функции можно разложить в ряды
1. Показательная функция:

на множестве всех действительных чисел R, т. е. на промежутке от


2. Тригонометрические функции.

на множестве всех действительных чисел R.

на множестве R.

на промежутке [-1, 1].
Из этого ряда при x = 1 получается знаменитый ряд Лейбница

- первый ряд, дающий разложение числа

Для вычисления числа


a)

б) ряд Леонардо Эйлера:

3. Логарифмическая функция

на промежутке (-1, 1).
4. Разложение бинома в ряд или биномиальный ряд:

на промежутке (-1, 1), где m - любое вещественное число, отличное от 0 и от всех натуральных чисел (при натуральном m получается известное разложение по формуле Ньютона - бином Ньютона).
Вы уже знакомы с последовательностями, которые задавались формулами n-го члена этих рядов и находили члены этих последовательностей. Это обстоятельство упростит нам процесс составления программ суммирования рядов.
Совершенно ясно, что с помощью этих рядов можно вычислять значения соответствующих функций.
Возникает следующий вопрос. Как оценить точность, с которой надо найти значение функции?
Математика также дает на этот вопрос ответ.
Пусть требуется вычислить значение функции ex с точностью до eps, где eps любое положительное число (в частности, eps может быть равно 0,1, 0,01, 0,001, 0,0001 и т.д.).
Для вычисления ex с заданной степенью точности eps необходимо n членов ряда, тогда можно записать, что приблизительно

Оставшиеся члены ряда можно обозначить rn(x) и назвать остатком ряда или остаточным членом, или дополнительным членом.
Чему равен этот остаточный член? Совершенно очевидно, что он по абсолютной величине будет меньше или равен заданной точности вычисления, т.е.
числу eps,

с помощью данного ряда.
Можно записать, что

Математика дает несколько формул дополнительного члена различных рядов. Для этого ряда дополнительный член может быть
записан в следующем виде:



При x>0 погрешность по этой формуле оценивается так:

В частности, при x = 1,


Подумайте, почему в числителе дроби дополнительного члена оказалось число 3?
С помощью этой формулы можно с большой степенью точности вычислить число e.
Пример 1. Составим программу вычисления числа e по этой формуле.
Прежде найдем рекуррентную формулу, связывающую предыдущий и последующий члены ряда.
Это сделать нетрудно:


Алгоритм
1. Начало.
2. Установить переменные и их типы.
Переменная n будет участвовать в получении членов ряда и должна иметь целый тип (integer).
Переменная eps задает точность, с которой подсчитывается сумма ряда, т.е. значение числа e. Она имеет вещественный тип.
Нужна переменная, в которую будут последовательно заноситься члены ряда. Эту переменную обозначим u. Она будет иметь вещественный тип.
И, наконец, переменная e - результат вычисления, т.е. сумма ряда имеет вещественный тип.
3. Основная программа, в которой вычисляется сумма членов ряда.
1). Ввод пользователем точности, с которой должно быть вычислено значение e. Оно присваивается переменной eps.
2). Для вычисления суммы ряда организуем цикл с последующим условием. Перед началом цикла установим переменным n и u первоначальные значения, которые равны 1, а переменной e - значение 0 (ведь в переменной e будет накапливаться сумма членов ряда).
3). В цикле подсчитывается сумма, "вырабатывается" следующий член ряда и увеличивается значение n на единицу.
4). Условие в конце цикла должно связывать заданную точность вычисления - eps и остаток ряда

5). Вывод информации.
4. Конец.
Программа
Program
Problem1; {Вычисление числа e}
uses WinCrt;
var
n : integer;
e, u, z, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
begin
write('Задайте точность вычисления '); readln(eps);
e := 0; u := 1; n := 1;
repeat
e := e+u;
u := u/n; n := n+1
until 3*u <= eps;
write('Число e равно ', e:3:t(eps));
writeln(' с точность до ', eps:1:t(eps))
end.
Задание 1
Вы уже знаете, что значения sinx можно вычислять с помощью следующего ряда:


Так как ряд знакочередующийся, то его остаток меньше по абсолютной величине последнего "отброшенного" члена, т. е. n + 1 - го.
Составьте программу вычисления значений sinx с заданной степенью точности eps для различных, вводимых пользователем значений x.
Пример 2. С помощью биномиального ряда, в который разлагается двучлен

Надо лишь помнить, что значения x принадлежат промежутку (-1, 1), на котором рассматривается биномиальный ряд.
Для примера посмотрим, как вычислить значение корня кубического из числа 10, т.е.

Прежде надо преобразовать подкоренное выражение к виду

=8, и тогда


Полученное выражение можно разложить в биномиальный ряд и вычислить с любой степенью точности.
Осталось выяснить вопрос относительно оценки точности вычисления с помощью дополнительного члена. Для этого снова обратимся к разложению и его остатку.

Этот ряд также знакочередующийся, значит остаток по абсолютной величине меньше абсолютной величины n + 1 - го члена.

Нетрудно найти рекуррентную формулу для получения членов этого ряда.
Она будет такой:

Теперь составим программу для вычисления корней с помощью этого ряда.
Программа
Program Problem2;
uses WinCrt;
var
n : integer;
x, m, z, eps, u, b : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите значение x, |x|<1 '); readln(x);
write('Введите значение дробного показателя m '); readln(m);
write('Задайте точность вычисления '); readln(eps);
b := 1; u := 1; n := 1;
repeat
u := (m - n + 1)*x*u/n;
b := b + u;
n := n+1
until abs(u) <= eps;
writeln('Корень', 1/m:3:0, ' - й степени из ', (1 + x):3:t(eps));
writeln(' равен ', b:3:t(eps),' с точностью до ', eps:3:t(eps))
end.
Задание 2
Составьте программу, которая вычисляет значение числа

при помощи ряда Лейбница:

Геометрические вероятности "геометрическая схема" испытания
"Классическая схема", основанная на понятии равновозможности конечного числа исходов испытания, при изучении большинства явлений реального мира является недостаточной. На практике часто встречаются такие испытания, исходы которых, как правило, являются или неравновозможными, или их число бесконечно.
Так, если испытание состоит в том, что сигнальщик в течение часа должен принять мгновенный световой сигнал, то его возможными исходами можно считать появление сигнала в любой момент времени в течение этого часа. Если испытание состоит в том, что разведчик должен нарушить линию связи длиной 2 км, то возможными исходами этого испытания можно считать разрыв линии связи в любой точке.
Множество исходов таких и аналогичных им испытаний бесконечно. Оно может быть иллюстрировано геометрически в виде совокупности точек отрезка прямой, плоской фигуры или пространственного тела. В связи с этим такую схему испытания принято называть геометрической схемой.
Вероятности, вычисляемые как отношения мер. Пусть в результате испытания наудачу выбирается точка в области S. Требуется найти вероятность того, что эта точка окажется в области s, являющейся частью области S.
Как указывалось в первом пункте, мы будем рассматривать области одного, двух и трех измерений. Так как число возможных исходов таких испытаний и число исходов, благоприятствующих рассматриваемым событиям, бесконечно, то формулу для непосредственного подсчета вероятностей применять нельзя.
Введем следующее допущение. Пусть исходы испытания распределены равномерно. Это значит, что если разделить некоторую область S на конечное число равновеликих частей si, (i= 1, 2, 3, ..., n), то событие Ei, означающее попадание наудачу выбранной точки из области S в любую область si ее часть, равновозможны, т.е. можно считать, что вероятность попадания наудачу выбранной точки из области S в какую-либо часть s этой области пропорциональна мере это части и не зависит от расположения и формы.
Следовательно,

где

Прежде, чем перейти к рассмотрению примеров с использованием понятия геометрической вероятности рассмотрим стандартную функцию и процедуру, которые используются в Турбо Паскале.
Гипергеометрическое распределение
Биномиальное распределение вероятностей точно только при условии отбора изделий по схеме случайной повторной выборки.
На практике изделия для проверки отбираются по схеме случайной бесповторной выборки, т.е. изделия из партии отбираются каждый раз случайно, но отобранные изделия не возвращаются в партию.
Схема случайной бесповторной выборки приводит уже не к биномиальному, а к так называемому гипергеометрическому закону распределения.
Пример 1. В урне находится N шаров, из которых M белых. Пусть один за другим без возврата (или одновременно, что одно и то же) вынимается n



Для вычисления гипергеометрических вероятностей найдем рекуррентную формулу для вычислений. Здесь тем более могут получаться очень большие числа.
Логика рассуждений будет такая же, как и при нахождении подобной формулы для биномиального закона распределения.

отсюда получаем:

Для начального значения, при m = 0, находим:


Надо заметить, что если число изделий в партии велико, а число отобранных изделий составляет весьма малую долю всей партии, поэтому расчет вероятностей по формулам биномиального распределения дает достаточно хорошие приближения.
{ Гипергеометрический закон распределения вероятностей }
Program Problem1;
uses WinCrt;
var
p, s, s1, s2 : real;
nn, mm, n, m, k : longint;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа сочетаний из n элементов по k }
Procedure
Combination(n, k : integer; var s : real);
var
i : longint;
begin
s := 1;
if k = 0 then s := 1
else for i := 1 to n - k do s := s*(k + i)/i
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите число всех шаров в урне '); readln(nn);
write('Введите число всех белых шаров в урне '); readln(mm);
write('Введите число извлекаемых из урны шаров ');
readln(n);
writeln('Введите число белых шаров, вероятность');
write('получения которых Вы хотите найти '); readln(k);
Combination(nn, n, s); Combination(mm, k, s1);
Combination(nn - mm, n - k, s2);
p := (s1*s2)/s;
writeln;
writeln('Вероятность того, что среди вынутых ', n);
writeln('шаров будет ', k, ' белых шаров, равна ', p:1:6)
end.
Математическое ожидание гипергеометрического распределения равно

Дисперсия определятся формулой:

Арифметические операции
В языке Паскаль используются целые числа, к которым относятся все натуральные числа, образовавшиеся в процессе подсчета предметов: 1, 2, 3, 4, 5, 6, ...; отрицательные числа: ..., -6, -5, -4, -3, -2, -1 и число ноль: 0. Целые числа образуют следующий ряд:
..., -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, ...
В Паскале допускается диапазон целых чисел от -32768 до 32767.
Переменные, принимающие целые значения, записываются в разделе описаний с указанием типа integer (целый).
Например: var a, b, c, a1, b34, nomb: integer;
Значения другого типа этим переменным в одной программе присвоить нельзя.
Числовые и функциональные ряды
Снова сделаем небольшую экскурсию в математику и познакомимся с числовыми и функциональными рядами.
Определение. Пусть задана некоторая бесконечная последовательность чисел

Составленный из этих чисел символ или сумма

называется бесконечным рядом, а сами числа - членами ряда.
Вместо записи (2), пользуясь знаком суммы, можно записать так:




Примеры
числовых рядов.
1. Простейшим примером бесконечного ряда является геометрическая прогрессия:

2.

3. Следующий ряд называется гармоническим:

4. Ряды могут быть не только с положительными членами, но и знакопеременными. Вот простейшие примеры таких рядов:
a)

б)

в)

г)


Числовые последовательности
Начнем с определения последовательности. Определений числовой последовательности дается много, причем самых разных и достаточно понятных, но, по моим соображениям, самое лучшее с точки зрения и математической строгости и доступности дается в книге: "Курс дифференциального и интегрального исчисления", т. 1 Г.М. Фихтенгольца. Я привожу его с незначительными изменениями.
Представим себе натуральный ряд:
1, 2, 3, ..., n, ..., n', ...,
в котором числа расположены в порядке возрастания, так что большее число n' следует за меньшим числом n (или меньшее n предшествует большему числу n'). Если теперь заменить в этом ряде, по какому-нибудь закону каждое натуральное число n некоторым вещественным числом xn , то получится числовая последовательность:
x1, x2, x3, ..., xn, ..., xn', ...,
члены или элементы которой xn занумерованы всеми натуральными числами и расположены в порядке возрастания номеров. При n'>n, член xn' следует за членом xn (xn предшествует xn' ), независимо от того, будет ли само число xn' больше, меньше или даже равно числу xn.
В школьном курсе математики вы уже знакомились с последовательностями вида

или вида

В связи с определением длины окружности обычно рассматривается переменный периметр правильного вписанного в окружность многоугольника, получаемого из шестиугольника последовательным удвоением числа сторон; таким образом, получается следующая последовательность:

Упомянем еще о десятичном приближении (скажем, по недостатку) к


Иногда последовательность задается тем, что указывается непосредственно
выражение для xn; так, в случае арифметической или геометрической прогрессии имеем, соответственно,


В других случаях нам может быть неизвестно выражение для общего члена xn последовательности.
Тем не менее, последовательность считается заданной, если мы владеем правилом, по которому может быть вычислен любой ее член, лишь только известен его номер.
Поэтому-то, зная правило для приближенного вычисления корней, мы можем считать заданной всю последовательность десятичных приближений к

Если последовательность - в указанном смысле - задана, то этим не только охарактеризовано все множество принимаемых ею значений в целом, но и определен порядок, в котором эти значения принимаются; каждому номеру отвечает свое значение элемента последовательности, и из двух значений то считается следующим, номер которого больше.
Еще подчеркнем, что значения элементов последовательности не должны быть обязательно различными. Например, если задать последовательность одной из формул:

то соответствующие последовательности будут:

В первом
случае мы имеем просто постоянную величину, всё "множество" принимаемых ею значений сводится к одному.
Во втором
- это множество состоит из двух значений, 1 или -1, принимаемых поочередно. Наконец, в третьем случае множество значений бесконечно, но это не мешает значениям элементов через одно равняться 0; и мы считаем, что значение 0 на пятом месте следует не только за 1 на втором месте, но и за значением 0 на первом месте.
Еще один способ задания последовательности - это рекуррентная формула. Вспомним, что это такое.
Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной
(от латинского слова recurro - возвращаться).
Подводя итог вышеизложенного можно назвать три основных способа задания последовательности.
1. Аналитический
- последовательность задается формулой общего (или n-го) члена.
2. Рекуррентный
- любой член последовательности, начиная с некоторого, выражается через предшествующие члены. При этом способе задания последовательности указывают ее первый член или несколько начальных членов и формулу, позволяющую определить любой член последовательности по известным предшествующим членам.
3. Словесный
- задание последовательности описанием.
Надо сразу заметить, что для составления программ чаще нам придется использовать рекуррентное соотношение. Покажем это на примере.
Пример 1. Составить программу вывода на экран членов последовательности, заданной следующей формулой:

Для составления программы необходимо перейти от формулы n-го члена, которым задана последовательность к рекуррентному соотношению, связывающему предыдущий член с последующим и указать начальное значение для первого или "нулевого" элемента. Как это сделать? Оказывается очень просто!
1. Запишем, чему будет равен член последовательности предыдущий к n - му, т. е. n-1 - й элемент последовательности:

2. Теперь разделим n - й элемент на n-1 - й, получим:

3. Отсюда выразим, чему будет равен n-й член:

4. Найдем начальное значение


Процедуру можно построить из одного цикла с параметром, в котором каждый раз при выполнении цикла предыдущее значение будет умножаться на 10 и делится на значение переменной цикла, которая обозначена n.
Procedure Create_succession(k : integer);
var
n : integer;
a : real;
begin
a := 1;
writeln('Искомая последовательность');
for n := 1 to k do
begin
a := a*10/n;
write(a:6:6, ' ')
end;
writeln
end;
Программа
Program Problem1; {Вывод членов последовательности}
uses WinCrt;
var
k : integer;
{---------------------------------------------------------------------------------------}
Procedure Create_succession(k : integer);
var
n : integer;
a : real;
begin
a := 1;
writeln('Искомая последовательность');
for n := 1 to k do
begin
a := a*10/n;
write(a:6:6, ' ')
end;
writeln
end;
{---------------------------------------------------------------------------------------}
begin
write('Введите число элементов '); readln(k);
Create_succession(k);
end.
Пример 2. Составим программу вывода на экран членов последовательности, описываемой словесно, в частности, десятичных приближений числа

Вот здесь дело обстоит сложнее. Закон, по которому строится последовательность указан словесно. Надо от словесного задания правила перейти к рекуррентной формуле.
А есть ли формула для вычисления квадратных корней? Оказывается есть и достаточно простая.
Рассмотрим бесконечную последовательность x1, x2, x3, ..., образованную по следующему закону:

Оказывается, что члены этой последовательности с увеличением номера i всё меньше и меньше отличается от





Напомним, что

Мы можем, используя данное рекуррентное соотношение, составить процедуру и программу
вычисления квадратных корней для любого действительного подкоренного выражения, а не только 2.
Program Problem2;
uses WinCrt;
var
n : integer;
u : real;
{----------------------------------------------------------------------------------------}
Procedure Square_root(n : integer; u : real);
var
i : integer;
x : real;
begin
writeln('Десятичные приближ. с недост. кв. корня из ', u);
x := (u + 1)/2;
for i := 1 to n do
begin
x := (1/2)*(x + u/x);
write(x:3:i, ' ')
end;
writeln
end;
{---------------------------------------------------------------------------------------}
begin
write('Введите подкоренное выражение '); readln(u);
write('Введите число членов последовательн. '); readln(n);
Square_root(n, u);
end.
Вычислим приближенное значение квадратного корня из заданного числа с указанной точностью eps. Теперь нам не надо выводить на экран все члены последовательности, а выдать только одно значение удовлетворяющее указанной точности.
Например, поставлена задача получить квадратный корень из 2 с точностью до 0.01. На экран должно быть выдано значение этого корня (причем совсем не обязательно, чтобы в его записи было два знака после запятой, их может быть больше, но мы будем заведомо знать, что знаки после сотых долей не являются точными).
Такие программы
можно составить двумя способами.
Способ первый состоит в том, что цикл будет продолжаться до тех пор, пока разность между квадратом получаемого результата и подкоренным выражением по абсолютной величине не станет меньше или равна указанной точности eps. Тогда цикл заканчивается и выдается результат.
1-й способ
Program
Problem2a;
uses WinCrt;
var
u : longint;
x, eps : real;
{----------------------------------------------------------------------------------------}
Procedure Square_root1(eps, u : real; var x : real);
begin
x := (u + 1)/2;
repeat
x := (1/2)*(x + u/x)
until abs(x*x - u) <= eps
end;
{---------------------------------------------------------------------------------------}
begin
write('Введите подкоренное выражение '); readln(u);
write('Задайте точность вычисления '); readln(eps);
Square_root1(eps, u, x);
writeln('Квадратный корень из ', u, ' равен ', x:12:12);
writeln(' с точностью до ', eps:3:12)
end.
Во втором способе вычисляются два члена последовательности и их разность по абсолютной величине сравнивается с заданной точностью.
Как только эта разность станет равна или меньше указанной точности eps цикл заканчивается.
2-й способ
Program Problem2b;
uses WinCrt;
var
u : longint;
x, eps : real;
{----------------------------------------------------------------------------------------}
Procedure Square_root2(eps, u : real; var x : real);
var
x1, x2 : real;
begin
x1 := 1;
repeat
x1 := (1/2)*(x1 + u/x1);
x2 := (1/2)*(x1 + u/x1)
until abs(x2 - x1) <= eps;
x := x2
end;
{---------------------------------------------------------------------------------------}
begin
write('Введите подкоренное выражение '); readln(u);
write('Задайте точность вычисления '); readln(eps);
Square_root2(eps, u , x );
writeln('Квадратный корень из ', u, ' равен ', x:12:12);
writeln('с точностью до ', eps:3:12)
end.
Разберите содержание этих программ и выполните их на компьютере. В чем отличие этих двух способов? Какой из них вы считаете более рациональным и почему?
Измените каждую из этих программ так, чтобы на экран выдавались последовательно десятичные приближения корней с недостатком? С избытком?
Если вы внимательно разобрались в составлении и работе предыдущих программ, то могли заметить, что в программе примера 2, несмотря на то, что математически последовательность задана формулой n-го члена, используется рекуррентное соотношение. Указывается начальное значение a := 1, а затем каждый цикл предыдущее значение умножается на постоянный множитель:

Таким образом, при составлении программ чаще всего будет использоваться рекуррентное соотношение. Возникает закономерный вопрос. Как перейти от задания последовательности формулой n-го члена к рекуррентному соотношению?
Разберем этот процесс на частном примере.
Пример..
Пусть задана последовательность с помощью формулы n-го члена, например:


Разделим n-й член на (n-1)-й, получим:

Отсюда легко получить рекуррентную формулу:

Одной формулы недостаточно, еще необходимо задать некоторые начальные значения, первые члены последовательности, желательно нулевой член.
Получаем:


Итак, если последовательность задана формулой n-го члена, тогда, чтобы задать ее рекуррентной формулой, необходимо найти частное от деления n-го члена на (n - 1)-й, а затем умножить (n - 1)-й член на частное. Это произведение будет равно n-му члену и мы получаем нужную формулу. К ней необходимо добавить значение некоторых первых членов и, таким образом, последовательность будет задана. Коротко этот процесс можно записать так:

После выполнения программы вы, конечно, обратили внимание на то, что независимо от того какую точность вы указываете значение результата будут выдаваться с 12-ю знаками после запятой (такой формат задан в программе). И нам трудно определить сколько десятичных знаков являются верными.
Было бы очень удобно, указав точность, получать в результате только требуемое количество десятичных знаков, например, указав 0.001, мы получали бы в результате 3 знака после запятой и не более.
Это можно сделать с помощью следующей функции:
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
Ее работа проста. Введенное значение точности (eps) последовательно умножается на 10 до тех пор, пока ее значение не станет больше 1.
Например, для значения eps = 0.001 процесс определения порядка будет проходить так:

Переменная k подсчитывает число выполняемых циклов. Но число циклов будет на 1 больше, чем количество знаков после запятой. Почему? Да потому, что цикл выполняется до тех пор пока, пока значение eps станет больше 1. Это сделано из тех соображений, что значение eps никогда не станет точно равно 1, ибо для этой переменной установлен вещественный тип real, а это значит, что eps не будет равно целому числу, хотя в примере кажется, что

Фактическое значение в этом случае может выражаться числом 0.99999999... . Чтобы устранить неудобства, первоначальному значению k задано значение -1, а останов цикла выполняется после eps > 1.
Добавляя эту функцию в программу, легко использовать ее для вывода результата с требуемым числом десятичных знаков.
Тогда, две вышеприведенные программы могут быть построены так:
Program Problem2a;
uses WinCrt;
var
u : longint;
x, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{---------------------------------------------------------------------------------------}
Procedure Square_root(eps, u : real; var x : real);
begin
x := (u + 1)/2;
repeat
x := (1/2)*(x + u/x)
until abs(x*x - u) <= eps
end;
{---------------------------------------------------------------------------------------}
begin
write('Введите подкоренное выражение '); readln(u);
write('Задайте точность вычисления '); readln(eps);
Square_root(eps, u, x);
writeln('Квадратный корень из ', u, ' равен ', x:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
Program Problem2b;
uses WinCrt;
var
u : longint;
x, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{---------------------------------------------------------------------------------------}
Procedure Square_root(eps, u : real; var x : real);
var
x1, x2 : real;
begin
x1 := 1;
repeat
x1 := (1/2)*(x1 + u/x1);
x2 := (1/2)*(x1 + u/x1)
until abs(x2 - x1) <= eps;
x := x2
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите подкоренное выражение '); readln(u);
write('Задайте точность вычисления '); readln(eps);
Square_root(eps, u, x);
writeln('Квадратный корень из ', u, ' равен ', x:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
Задание 1
1. Составьте программы вывода на экран членов последовательности, задаваемых следующими способами:
1)

3) последовательность состоит из десятичных приближений с избытком частного

Пример 3. Рассмотрим бесконечную последовательность x1, x2,..., образованную по следующему закону:


где u - данное неотрицательное действительное число, n - натуральное число.
Эта последовательность позволяет получить сколь угодно точные приближения числа





{ Вычисление корня с любым натур. показат. действит. числа }
Program Problem3;
uses WinCrt;
var
u, n, eps, x : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Procedure Root(u, n, eps : real; var
x : real);
var
x1, x2, xn : real;
i : integer;
begin
x1 := (u + n - 1)/2;
repeat
xn := 1;
for i := 1 to trunc(n) - 1 do
xn := xn*x1;
x1 := ((n - 1)*x1 + u/xn)/n;
x2 := ((n - 1)*x1 + u/xn)/n
until abs(x1 - x2) <= eps;
x := x2
end;
{--------------------------------------------------------------------------------------}
begin
write('Введите подкоренное выражение '); readln(u);
write('Введите показатель корня '); readln(n);
write('Введите точность вычисления '); readln(eps);
Root(u, n, eps, x);
writeln('Значение корня равно ', x:8:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
Рассмотрим несколько последовательностей, заданных формулами n-го члена:

3)

4)


5)



Нам еще придется на следующем занятии иметь дело с этими последовательностями, но уже при постановке несколько иной задаче. А теперь составим программы вычисления членов последовательности, причем вычисления вести до того члена, который по абсолютной величине станет равным или меньше заданной точности. Выполним это задание для последовательностей 2-й и 4-й.
Пример 4.
Последовательность задана формулой

Вывести на экран члены последовательности до члена, меньшего заданного положительного числа eps. Желательно принять 0 < eps < 1.
Самое важное - это перейти от формулы n-го члена к рекурретному соотношению, которое впоследствии надо использовать при составлении программы.
Запишем формулу n-1 -го члена:

Разделим un
на un-1, получим:

тогда

Надо заметить, что первый член равен: u1 = x.
После этого нетрудно составить программу. Организуем цикл с предусловием "пока", пока |u| > eps. Почему для этой задачи удобно устроить именно такой цикл?
В нашем примере, в качестве начального значения берется первый элемент последовательности. Может случиться, что пользователь задал такое значение eps, что уже первый член меньше этого числа. И тогда вычислений выполнять не следует, т.е цикл не выполняется, а значит необходимо сразу проверить условие. Такое делается в цикле с предусловием. Цикл repeat ... until будет обязательно выполняться хотя бы один раз, а этого нам не нужно.
Программа
Program Problem4;
uses
WinCrt;
var
x, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Procedure
Create_succession(x, eps : real);
var
u : real;
n : integer;
begin
u := x;
n := 1;
while abs(u) > eps do
begin
n := n + 1;
write(u:6:t(eps), '; ');
u := (-1)*u*x*x/((2*n - 2)*(2*n - 1))
end;
writeln
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите значения |x| <= 1 '); readln(x);
write('Задайте положит. число eps '); readln(eps);
writeln('Члены последовательности');
Create_succession(x, eps);
end.
Пример 5. Последовательность задана формулой:

где m - вещественное число, отличное от 0 и от всех натуральных чисел, при

Вывести на экран члены последовательности до члена, меньшего наперед заданного положительного числа eps, 0 < eps < 1.
Из формулы n-го члена составьте рекуррентную формулу, установите каким должно быть первоначальное значение, составьте программу и сравните ее с приведенной ниже программой.
Program Problem5;
uses WinCrt;
var
x, m, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Procedure
Create_succession(x, m, eps : real);
var
n : integer;
u : real;
begin
u := 1;
n := 1;
repeat
u := u*(m - n + 1)*x/n;
write(u:3:t(eps), ' ');
n := n + 1
until abs(u) <= eps;
writeln
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите значения x, |x| < 1 '); readln(x);
writeln('Введите вещественное положительное m, отличное от');
write('натуральных чисел '); readln(m);
write('Задайте положительное число eps '); readln(eps);
writeln('Члены последовательности');
Create_succession(x, m, eps)
end.
Задание 2
Составьте программы вывода на экран членов последовательности до члена, меньшего заданного положительного числа eps, 0 < eps < 1. Возьмите для задания примеры 1, 3, 6:
1)

3)

6)



Усложним задачи и разберем следующий пример.
Пример 6. Дано положительное число eps. Последовательность a1, a2, a3,... образована по следующему закону:

Найти первый член an последовательности, для которого выполнено условие:

Составить программу выполнения этого задания.
Алгритм
1. Содержание.
а) Переменные и их типы. Переменная i принимает целые значения:

2. Основная часть.
а) Ввод значения eps.
б) Установить первоначальные значения переменных i, ap и an:
i := 1, ap := 1, an := 1 - 1/2.
в) Цикл "пока" с условием: abs(an - ap) >= eps.
Команды в цикле. Значения i каждый раз в цикле должны увеличиваться на единицу; значения ap := 1 - 1/i; значения an := ap*(1 - 1/(i + 1)).
г) После завершения работы цикла, вывод значения an на экран. Можно вывести и номер i этого члена последовательности.
3. Конец.
Составим процедуру и программу, используя алгоритм.
Программа
Program Problem6;
uses
WinCrt;
var
i : integer;
a, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until
eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Procedure
Create_succession(eps : real; var i : integer; var a : real);
var
i : integer;
an, ap : real;
begin
i := 1; ap := 1; an := 1 - 1/2;
while abs(an - ap) >= eps do
begin
i := i + 1;
ap := ap*(1 - 1/i);
an := ap*(1 - 1/(i + 1))
end;
a := an
end;
{---------------------------------------------------------------------------------------}
{ Основная программа }
begin
write(' Введите любое положительное число eps '); readln(eps);
Create_succession(eps, i, a);
writeln('Искомый член последовательности ', a:6:t(eps));
writeln('Находится на ', i, '-ом месте в последовательности')
end.
Задание 3
Последовательность задана формулой:


Если Вы составили программу и выполнили ее несколько раз, то смогли убедиться в том, что для любого положительного числа eps найдется член последовательности yN, такой, что модуль разности (yN- 2) меньше eps.
Дополним программу так, чтобы она показывала, что неравенство


Но перед этим, вспомним определение предела последовательности.
Определение предела последовательности
Число A называется пределом последовательности xn, если для любого положительного числа


Последнее неравенство равносильно следующему:

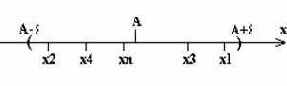

Рис. 42
Какой бы малый отрезок (длиной

Точка, изображающая предел A, является как бы средоточением сгустка точек, изображающих значения членов последовательности.
Возвращаясь к примеру 5, можно сказать, что по сути дела мы показывали, что число 2 является пределом последовательности

Если эту программу немного изменить, то она станет такой.
Пример 7. Программа, показывающая, что пределом последовательности

Program Problem7;
uses
WinCrt;
var
i, n, k : longint;
eps, yn, yp : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until
eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
writeln('Введите произвольное положительное число, ');
write('можно даже очень малое '); readln(eps);
i := 1; k := -1; yn := 1;
while
abs(yn - 2) >= eps do
begin
i := i + 1; k := k*(-1);
yn := 2 + k/i
end;
writeln('Условию abs(yn-2)<', eps:1:t(eps), ' удовлетворяет');
writeln('член последовательности yn = ', yn:6:t(eps), ',');
writeln('находящийся под номером ', i); writeln;
write('Введите номер члена последовательности больше ',i,' ');
readln(n);
if
n mod 2 = 0 then yn := 2 + 1/n else yn := 2 - 1/n;
if
abs(2 - yn) < eps
then
begin
write('Неравенство abs(2 - ', yn:6:t(eps), ') < ', eps:1:t(eps));
writeln( ' выполняется ')
end
else
begin
write('Неравенство abs(2 - ', yn:6:t(eps), ') < ', eps:1:t(eps));
writeln(' не выполняется')
end
end.
Задание 4
Составьте программу, показывающую, что число 1 является пределом последовательности

Продолжим составление программ на последовательности и немного усложним задачу. Если в двух предыдущих примерах заведомо было известно число, которое является пределом последовательности, то в следующем примере надо будет определить существует ли вообще предел и если существует, тогда найти его и показать, что оно действительно является пределом заданной последовательности.
Таким образом, задача имеет две части:
1) установить существование
предела и,
2) если таковой существует, то показать чему он равен.
Перед выполнением такого задания обратимся к курсу математического анализа, в котором есть теорема, которая принадлежит чешскому математику Больцано и французскому математику Коши, ее часто называют принципом сходимости. Она выражает общий
Признак существования конечного предела последовательности
Пусть задана последовательность xn, пробегающая значения x1, x2, ..., xn, ..., xm, ... Для того, чтобы последовательность xn имела конечный предел, необходимо и достаточно, чтобы для каждого числа




между собой безгранично сближались по мере возрастания их номеров.
Этот признак допускает простую геометрическую иллюстрацию (рисунок 43).
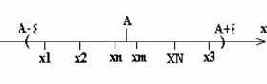
Рис. 43
Пример 8. Выяснить имеет ли предел последовательность, заданная формулой:

Алгоритм решения основывается на признаке существования предела последовательности. Нам необходимо установить, что члены последовательности по мере увеличения номера сближаются друг с другом. Перекладывая это на язык математики, нам надо задать положительное число eps, которое может быть сколь угодно малым и найти такие два члена последовательности, разность между которыми по абсолютной величине будет меньше этого наперед заданного, может быть даже, очень малого числа eps.
Идея становится понятной. Остается продумать, как находить члены последовательности в зависимости от их номеров?
Конечно, можно составить рекуррентное соотношение, но это будет немного трудным делом чисто в математическом отношении.
Возникает другая мысль. Составить подпрограмму возведения в степень и из основной программы каждый раз обращаться к ней для вычисления степени с изменением номера n. Тем более, что опыт составления подпрограмм у нас уже есть. Мы достаточно много составляли на прошедших занятиях подпрограмм в форме процедур и функций.
Основная программа. Вначале попросим пользователя задать точность вычисления (так мы назвали число eps).
Затем задается начальное значение переменной n (n := 1). Организуется цикл с последующим условием (repeat ... until...), в котором переменной x - члену последовательности присваивается значение, вычисляющее значение функции



Проверяется условие abs(x1 - x) < eps. Как только условие выполнится, цикл закончится и в качестве значения предела последовательности мы можем брать любое из значений x или x1 и оно укажет нам значение предела последовательности с заданной точностью eps.
Если кто-нибудь из вас раньше встречался с такой последовательностью, то он сразу был уверен, что ее предел существует и равен числу e - основанию натурального логарифма.
Проверьте это, выполнив программу
Program
Problem8;
uses WinCrt;
var
n : integer; x, x1, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Function s(k: integer; p : real) : real;
var
i : integer; z : real;
begin
z := 1;
for i := 1 to k do z := z*p;
s := z
end;
{----------------------------------------------------------------------------------------}
begin
write('Задайте точность '); readln(eps);
n := 1;
repeat
x := s(n, (1 + 1/n));
n := n + 1;
x1 := s(n, (1 + 1/n))
until abs(x1 - x) < eps;
writeln('Предел последовательности равен ', x1:6:t(eps));
writeln('С точностью до ', eps:1:t(eps))
end.
Задание 5
Последовательность un принимает значения

Показать, что un
стремится к некоторому пределу при

(При составлении программы использовать в качестве подпрограммы функцию вычисления степени числа 3 с показателем n).
Цикл с последующим условием Оператор repeatuntil
1. Оператор цикла с последующим условием (постусловием) похож на оператор цикла с предусловием, но условие вычисляется и проверяется после выполнения операторов, составляющих тело цикла.
Общий вид оператора цикла с постусловием такой:
repeat
s1; s2; s3; ..
until <условие>,
где s1, s2, s3, ... - операторы тела цикла; <условие> - логическое выражение.
Переводится: repeat
- повторять, until - до тех пор пока.
Как видите, такой цикл начинается с выполнения операторов внутри цикла, а уже затем вычисляется выражение, записанное в условии.
Если значение этого выражения истинно, тогда осуществляется выход из цикла, если значение ложно, то цикл продолжается и снова выполняются операторы

Надо сразу заметить, что в отличии от цикла while ... do, в цикле repeat
... until ... операторные скобки begin ... end могут не использоваться, хотя и использование их вреда не принесет. Можно сказать другими словами, что оператор цикла repeat ... until. ... не требует операторных скобок begin ... end.
Рассмотрим работу этого оператора на примере.
Пример 1. Найти наименьшее натуральное число, дающее при делении на 2, 3, 4, 5, 6 соответственно остатки 1, 2, 3, 4, 5.
Задачу будем решать так: берется наименьшее натуральное число - единица и находятся остатки от деления его на 2, 3, 4, 5 и 6; если остатки будут равны 1, 2, 3, 4 и 5, тогда это число является искомым, его надо выдать на экран и закончить программу, в противном случае, надо брать следующее натуральное число - 2 и проверять его, и так далее.
Программа, составленная по этой идее, очень проста:
Program Problem1;
uses WinCrt;
var
n : integer;
begin
n := 0;
repeat
n := n + 1;
until (n mod 2 = 1) and (n mod 3 = 2) and (n mod 4 = 3) and
(n mod 5 = 4) and
(n mod 6 = 5);
writeln('Искомое целое число ', n)
end.
Еще один пример, который демонстрирует работу цикла с постусловием.
Пример 2. Числа, одинаково читающиеся и слева направо, и справа налево, называются палиндромами. Например, числа 42324 или 1331 - палиндромы. Составьте программу, которая будет находить числа - палиндромы из заданного промежутка.
Логика составления программы такова.
Переставить цифры в числе и сравнить полученное число с заданным.
Раньше уже составлялась программа перестановки цифр числа, которая была выполнена с помощью цикла с предусловием
while ... do
...
Как будет построена часть программы о перестановки цифр с помощью цикла
repeat ... until ...
Пусть заданное число a, тогда введем еще одну переменную b, которой будет присвоено значение переменной a (для чего это делается вы узнаете позже): b := a;
Заведем еще одну переменную a1 для нового числа, в котором цифры уже будут переставлены.
Первоначальное значение этой переменной - ноль: a1 := 0;
Почему значение этой переменной равно нулю станет ясно из программы.
Далее организуем цикл repeat, в котором будет происходить перестановка цифр числа b:
repeat
a1 := a1*10 + b mod 10;
b := b div 10
until b = 0;
Итак, в цикле, также как и в цикле while ... do ..., отделяется последняя цифра:
b mod
10; (например, 343 mod 10 = 3); переменной a1 присваивается значение:
a1 := a1*10 + b mod
10; 0 * 10 + 3 =3;
"отбрасывается" последняя цифра заданного числа с помощью операции целочисленного деления:
b := b div 10; 343 div 10 = 34;
проверяется условие: b = 0, 34 = 0, условие не выполняется, значит цикл продолжается.
Отделяется последняя цифра уже нового числа:
b mod 10 = 34 mod 10;
новое число a1, уже равное 3, умножается на 10 и к результату прибавляется следующая цифра - 4:
a1 := a1*10 + b mod
10;
"отбрасывается" последняя цифра числа b:
b := b div 10 ; 34 div 10 = 3;
проверяется условие: b = 0, 3 = 0; условие не выполняется, значит цикл продолжается.
Отделяется последняя цифра числа:
b mod 10 ; 3 mod
10 = 3;
формируется новое число:
a1 := a1*10 + b mod 10 ; 34 * 10 + 3 = 343;
"отбрасывается" последняя цифра числа и получается новое число:
b := b div 10 ; 3 div 10 = 0;
проверяется условие: b = 0, 0 = 0; условие выполняется, значит цикл заканчивается.
Теперь становится ясно, почему введена другая переменная b для заданного числа, ее значение в цикле меняется от начального до нуля и, чтобы сохранить заданное число в переменной a, и вводится, так сказать, "рабочая" переменная - b.
После окончания цикла перестановки цифр числа, сравнивается первоначальное число, которое "сохранилось" в переменной a и число, которое получилось после перестановки цифр и "накопилось" в переменной a1.
Если
a = a1, тогда значение a выдается на экран, так как это число является палиндромом.
Далее, значение a увеличивается на 1, т. е. берется для рассмотрения следующее по порядку натуральное число и снова продолжается внешний цикл. Цифры числа переставляются, полученное новое число после перестановки цифр - a1, сравнивается с первоначальным a и так далее.
Внешний цикл заканчивается, когда значение a становится равным правой границе интервала - n.
Составим
программу
Program Problem2;
uses WinCrt;
var
m, n, a, b, a1 : longint;
begin
write('Введите левую границу промежутка '); readln(m);
write('Введите правую границу промежутка '); readln(n);
a := m;
writeln('Числа палиндромы из [', m, ';', n, ']');
repeat
b := a; a1 := 0;
repeat
a1 := a1*10 + b mod 10;
b := b div 10
until b=0;
if a1 = a then write(a, ' ');
a := a + 1
until a > n;
end.
Программы, составленные с циклом с предусловием (while ... do...), легко можно переделать с циклом с постусловием (repeat ... until ...) и они будут такими:
Программа, подсчитывающая сумму цифр числа:
Program Sum; { Сумма цифр числа }
uses WinCrt;
var
n, s, a : integer;
begin
write('Введите целое число '); readln(n);
a := n; s := 0;
repeat
s := s + n mod 10; n := n div 10
until n = 0;
writeln('Сумма цифр числа ', a, ' равна ', s)
end.
Программа
перестановки первой и последней цифр в числе:
Program Transpose;
uses WinCrt;
var
n, n1, p, a, i : longint;
begin
write('Введите натуральное число n '); readln(n);
a := n; i := 1;
p := n mod
10; {последняя цифра введенного числа}
repeat
i := i*10; n := n div 10
until n<10;
n1 := a - n*i - p + n + p*i;
writeln('Число после перестановки цифр ', n1)
end.
Схематически цикл repeat можно изобразить так (см. рис. 21):
Рис. 21
Циклы с параметрами Операторы fortodo и fordowntodo
1. Иногда заранее известно, сколько раз должен выполняться цикл. Для задач такого типа в языке Паскаль имеются операторы циклов с параметрами.
Формат записи таких операторов следующий:
for <пар.цикла> := <нач.знач> to <кон.знач.> do <оператор>.
Здесь for, to, do - зарезервированные слова (для, до, выполнить);
<пар. цикла> - параметр цикла - переменная типа integer (точнее, любого порядкового типа);
<нач. знач.> - начальное значение - число или выражение того же типа;
<кон. знач.> - конечное значение - число или выражение того же типа;
<оператор> - произвольный оператор Паскаля.
Если операторов несколько, тогда, как и в операторе while ... do ..., используются операторные скобки: begin ... end.
Например, возможны такие записи оператора цикла:
for i := a to b do s1;
for j := a to b do begin
s1; s2; ..., sn end; или
for k := p to m do
begin
s1;
s2;
...
sn
end;
Здесь s1, s2, s3, ... sn - операторы цикла.
При выполнении оператора for вначале вычисляется выражение <нач .знач.> и осуществляется присваивание его значения переменной цикла
<пар .цикла> := <нач. знач.>.
После этого циклически повторяются:
1) проверка условия <пар .цикла>

2) выполнение оператора <оператор> или операторов s1; s2; s3; ... sn;
3) переменная цикла <пар. цикла> увеличивается на единицу.
Надо сразу заметить, что задать шаг цикла, отличный от 1 в этом операторе, нельзя.
Для иллюстрации работы оператора for рассмотрим пример уже ставший традиционным при изучении работы этого оператора.
Пример 1. Составить программу вычисления факториала числа n, т. е. n!.
Вспомним из математики, что факториал числа n равен произведению чисел от 1 до n.
Например:

Замечание.
В математике принято: 0! = 1.
Программа
Program
Problem1; { Вычисление факториала числа n! }
uses WinCrt;
var
n, f, i : longint;
begin
write('Введите натуральное число '); readln(n);
f := 1;
if n <> 0 then for i := 1 to
n do f := f*i;
writeln('Факториал числа ', n, ' равен ', f)
end.
Переменная n - для вводимого пользователем числа, факториал которого надо найти; f - переменная, в которой будет "накапливаться" значение факториала числа n; i - переменная цикла.
Устанавливается первоначальное значение переменной f := 1.
Далее начинается цикл. Переменной i присваивается начальное значение 1; оно сравнивается с конечным - n (1 <= n), если условие истинно, тогда
выполняется оператор (в этой программе он один): f := f*i, 1*1=1; значение переменной цикла увеличивается на 1, т. е. станет равным: i := i + 1, 1 + 1 = 2 и цикл повторяется.
Когда
значение i станет равным n, тогда цикл выполнится последний раз, потому что следующее значение i будет n + 1, что больше конечного значения n, условие
i <= n - ложно, цикл не выполняется.
Элементы комбинаторики
Здесь мы рассмотрим некоторые примеры из очень обширного круга задач, для решения которых используются ЭВМ и персональные компьютеры. Это вопросы комбинаторики и теории вероятностей.
Подпрограммы на паскале Процедуры и функции Рекурсия
1. Дедуктивный метод программирования
Отвлечемся на некоторое время от составления программ и поговорим о творческом процессе вообще, не только программиста или математика, а, например, художника или архитектора.
Допустим, что художник собирается нарисовать картину: портрет человека или что-то другое. Прежде, в глубине его сознания созревает общий образ будущего произведения, затем начинается ее реальное воплощение на холсте, бумаге, дереве или на чем-то другом. И вот здесь начинается тяжелейшая работа. Художник выполняет эскизы, рисунки отдельных фрагментов картины, а потом создает единое произведение, воплощающее в красках, цвете и тени, выношенный им образ.
Архитектор задолго до создания проекта своей новой конструкции также видит его целиком, а затем воплощает по отдельным частям единый проект здания или сооружения.
Подобно им и программист должен видеть в целом программу, которая решает какую-то задачу, а потом разбивает ее на отдельные части, составляет на выбранном языке программирования эти части программы, объединяет их в единое целое и получает программу.
Итак, весь творческий процесс можно разбить (разумеется, чисто условно) на следующие этапы:
1) основная идея решения задачи;
2) общая конструкция программы;
3) выделение отдельных, элементарных частей программы;
4) практическая реализация на языке программирования этих частей программы;
5) объединение их в единую программу.
Такой процесс программирования называют структурным или нисходящим. Более подробно с этим процессом мы познакомимся позже, когда изучим хотя бы основы языка программирования, но об отдельных частях, "кирпичиках", составляющих программу узнаем на этом занятии.
Подпрограммой называется группа операторов, к которой обращаются из основной программы несколько раз. Иногда это может быть 2, 3 раза, а очень часто, каждый раз из выполняемого цикла основной программы.
Вполне понятно, что писать несколько раз одинаковые группы операторов трудно, проделывается много "технической" работы, а в некоторых случаях просто невозможно (если обращаться приходиться каждый раз при выполнении цикла).
Для облегчения такой работы и созданы подпрограммы.
Использование подпрограмм позволяет:
1) сделать основную программу более наглядной и компактной;
2) уменьшить объем используемой памяти ЭВМ;
3) сократить время отладки программы.
На языке Паскаль подпрограммы бывают двух видов, - это процедуры и функции.
2. Процедуры
Рассмотрим следующий простой пример, с помощью которого попробуем разобраться в конструкции процедур на Паскале.
Пример 1. Составить программу, которая бы проверяла, являются ли три числа взаимно простыми.
Мы знаем, что числа называются взаимно простыми, если их наибольший общий делитель (НОД) равен 1. Значит, для решения этой задачи нам придется дважды находить НОД чисел. Если заданы три числа: a, b, c, то найти НОД(a, b), а затем найти НОД(НОД(a, b), c).
Дважды писать операторы для нахождения НОД нам не хочется, поэтому оформим операторы для НОД в виде процедуры.
Посмотрите, как это будет выглядеть в программе:
Program Problem1;
uses WinCrt;
var
a, b, c, k : integer;
{----------------------------------------------------------------------------------------}
Procedure nod(a, b : integer; var n : integer);
var
r : integer;
begin
repeat
r := a mod b;
a := b; b := r
until b = 0;
n := a
end;
{---------------------------------------------------------------------------------------}
begin
write('Введите три натуральных числа '); readln(a, b, c);
nod(a, b, k);
a := k; b := c;
nod(a, b, k);
if k = 1 then writeln('Числа взаимно простые')
else writeln('Числа не взаимно простые')
end.
В разделе описаний, после описания переменных, записывается заголовок процедуры: Procedure
Это слово является служебным и зарезервировано в Паскале. В одной строке с ним, через пробел, записывается имя процедуры, которое должно удовлетворять всем требованиям, предъявляемым к именам, основными из которых являются: начинаться с буквы и не иметь пробелов, т.
е., требования такие же, как и к имени программы (имя нашей процедуры - nod):
Procedure nod(a, b : integer; var
n : integer);
Далее, в скобках, записываются имена переменных и их типы, значения которых будут вводиться
в процедуру из основной программы, в нашем случае, их две (a, b) и они имеют тип integer.
Сразу надо заметить, что имена этих переменных могут не совпадать с именами переменных в основной программе, скажем мы могли их обозначить m, n или любыми другими именами.
После точки с запятой и зарезервированного слова var, записываются переменные и их типы, значения которых будет являться результатом работы процедуры и выводятся
из нее в основную программу. Такая переменная в нашем примере одна - n. Она выведет значение НОД чисел a и b. Ее имя также может иметь одноименное в основной программе и это нисколько не отразится на работе процедуры.
Обратите внимание, что перед переменными, значения которых вводятся из основной программы, не ставится слово var, а перед переменной, значение которой выводится
в основную программу, это слово записано. Это очень важное обстоятельство!
Так, если поставить var перед a и b, то компилятор будет воспринимать эти переменные как выходные и вводимые для них значения воспринимать не будет, и, наоборот, если var не будет записано перед выходной переменной, то компилятор воспримет ее как входную и выводить ее значение в основную программу не будет.
Дальнейшее построение процедуры строится также, как и основная программа на Паскале.
Описываются переменные, которые будут участвовать в ее работе, но их имена не должны повторять имена уже описанных входных и выходных параметров в заголовке программы. Далее описываются необходимые для работы операторы.
В нашем примере процедура nod будет такой:
Procedure nod(a, b : integer; var
n : integer);
var
r : integer;
begin
repeat
r := a mod b;
a := b; b := r
until b = 0;
n := a
end;
Основная программа строится обычным образом, но там, где необходимо найти НОД чисел, обращается к процедуре. Как?
Для этого обращаются к ней по имени, а в скобках записывают фактические значения входных переменных (в нашем случае для переменных a и b), а также имена выходных переменных (в нашем случае k).
Из приведенного ниже участка программы видно, что при первом обращении к процедуре nod определяется НОД чисел a и b (nod(a, b, k) и результат запоминается в переменную k, далее, изменяются значения переменных a и b


Вы можете видеть основную часть программы:
begin
write('Введите три натуральных числа '); readln(a, b, c);
nod(a, b, k);
a := k; b := c;
nod(a, b, k);
if k = 1 then writeln('Числа взаимно простые')
else writeln('Числа не взаимно простые')
end.
Сделаем общие выводы для построения и работы процедур
Процедуры помещаются в разделе описаний и начинается зарезервированным (служебным) словом
Procedure
Процедуре обязательно
дается имя, которое должно удовлетворять тем же требованиям, что и имена переменных, т.е. это может быть одна или несколько букв, комбинация букв и целых чисел, но без пробелов, начинаться с буквы и т.д.
После имени, в скобках записываются переменные - параметры и их тип: входные, значения которых используются для вычисления в качестве аргументов.
Выходные параметры - это те переменные, в которых получается результат выполнения процедуры.
Входные и выходные параметры процедуры называются формальными параметрами.
Фактические, конкретные, значения формальные параметры должны получить в основной программе после обращения к ней (а пока в процедуре они являются не чем иным, как "пустышками").
После формальных параметров, описываются переменные, которые необходимы непосредственно для работы процедуры.
Это параметры процедуры. Они нужны в ней, как и в любой другой программе и описываются также.
Их имена должны отличаться от имен входных и выходных параметров.
Надо заметить, что процедура может быть такой, что в ней не будет вообще параметров, достаточно тех, которые будут введены из программы.
Описание процедуры имеет вид:
Procedure <имя> (<входные параметры> : <их тип>;
var
<выходные параметры> : <их тип>);
(раздел описаний)
begin
(раздел операторов)
end;
Она помещается в основной программе в разделе описаний.
По входным и выходным параметрам процедуры могут быть следующих типов:
1) иметь и входные и выходные параметры:
Procedure
<имя>(<входные параметры> : <их тип>;
var
<выходные параметры> : <их тип>);
Мы только познакомились с программой такого типа.
2) иметь входные параметры, но не иметь выходных:
Procedure <имя>(<входные параметры> : <их тип>);
3) иметь выходные параметры, но не иметь входных:
Procedure
<имя>(var <выходные параметры> : <их тип>);
4) не иметь ни входных, ни выходных параметров:
Procedure
<имя>;
В зависимости от этого различаются процедуры по своей конструкции и выполняемым функциям.
Далее следует раздел операторов, который составляется по тем же правилам, как и в других программах.
Процедура описана и после этого начинается основная программа.
Вызов процедуры из программы
Как происходит вызов подпрограммы - процедуры?
Обязательно указывается имя процедуры. В скобках задаются фактические значения входных параметров и те переменные, в которые будут "запоминаться" выходные значения.
Рассмотрим пример, где может быть использована процедура второго типа: имеет входные параметры, но не имеет выходных.
Пример 2. Составить программу, которая устанавливает, какие числа из заданного промежутка [a; b] можно представить в виде суммы двух квадратов целых чисел?
В этой программе, нам придется проверять каждое из чисел промежутка [a; b] можно ли его представить в виде суммы квадратов двух чисел, поэтому было бы разумно разработать процедуру, которая бы проверяла одно число и затем обращаться к ней из основной программы для проверки каждого числа из промежутка.
Процедуру составим по следующему способу. Пусть задано число n. Нам необходимо найти такие два числа a и b, чтобы сумма их квадратов была равна n, т.е. решить в целых числах уравнение:

Возникает естественное желание испытывать натуральные числа от 1 и до ...? А вот до какого значения неизвестно. Если их брать до числа n, то это будет слишком много лишней и бесполезной работы.
Чтобы выяснить этот вопрос, можно организовать цикл, в котором проверять сколько чисел a
надо, чтобы выполнялось неравенство:

Этот цикл
может быть таким:
a := 1; k := 1;
while a*a + 1<=n do
begin
k := k + 1;
a := a + 1
end;
Теперь ясно, что для испытания чисел, следует устроить цикл от 1 до k:
for a := 1 to
k do
Второй цикл должен быть для значений b. Но если его организовать тоже от 1 до k, тогда могут повторяться дважды одинаковые значения, только на разных местах, например, для числа 20 могут быть выданы следующие значения:
22 + 42
= 20 и 42 + 22 = 20.
Чтобы избежать повторения чисел, цикл для чисел b можно организовать либо от 1 до a, либо от k до а.
Нами выбран первый вариант.
Процедура
Procedure
to_square(n : integer);
label 1;
var
a, b, k : integer;
begin
a := 1; k := 1;
while a*a + 1<=n do
begin
k := k + 1;
a := a + 1
end;
for a := 1 to k do
for b := 1 to a do
if a*a + b*b = n
then
begin
writeln(n, '=', a, '*', a,' +', b, '*', b); goto
1
end;
1: end;
Процедура выполнена с досрочным прерыванием цикла, так как нет необходимости выяснять всевозможные значения пар чисел, удовлетворяющих этому уравнению, а достаточно просто выяснить возможность такого представления.
Выполнив такую процедуру, не составляет труда решить полностью задачу. Для этого в основной программе выполнить цикл для всех чисел из промежутка, и каждое из которых, с помощью процедуры проверять. Кстати говоря, эта процедура имеет только один формальный параметр - входной, - значение проверяемого числа из промежутка и не имеет выходных параметров.
Программа
Program Problem2;
uses WinCrt;
var
a, b, i : integer;
{---------------------------------------------------------------------------------------}
Procedure to_square(n : integer);
label 1;
var
a, b, k : integer;
begin
a := 1; k := 1;
while a*a + 1 <= n do
begin
k := k + 1;
a := a + 1
end;
for a := 1 to k do
for b := 1 to a do
if a*a + b*b = n
then
begin
writeln(n, '=', a, '*', a, '+', b,'*', b); goto
1
end;
1: end;
{----------------------------------------------------------------------------------------}
begin
write('Введите начало промежутка '); readln(a);
write('Введите конец промежутка '); readln(b);
write('Числа, которые можно представить в виде суммы ');
writeln('квадратов следующих чисел');
for i := a to b do to_square(i);
end.
Структура программы на языке "Паскаль"
 |
На этом занятии мы познакомимся с конструкцией программ на языке программирования высокого уровня "Паскаль".
Этот язык разработал сравнительно недавно, в 1970 году, профессор кафедры вычислительной техники Швейцарского федерального института технологии - Николас Вирт.
Обо всех достоинствах и преимуществах Паскаля перед другими языками мы узнаем после первоначального знакомства с ним, в конце первой части этой книги, а теперь обратимся к составлению простейших программ на этом языке.
Изучение конструкции программ на Паскале начнем с простого примера.
Пример 1. Составить программу решения следующей задачи.
Саша спросил Сережу: "Сколько тебе лет?" Сережа ответил:
"Если бы число моих лет увеличить в 3 раза, а потом уменьшить на 17, то мне было бы 16 лет". Сколько лет Сереже?
Обычно решение такого типа задач начинается с "конца".
Число лет, которое было бы Сереже, т. е. 16, увеличиваем на 17, получаем

Полученный результат уменьшаем в 3 раза, т.е. делим на

Итак, Сереже было 11 лет.
Посмотрим, как будет выглядеть программа решения этой задачи на языке Паскаль.
Program Serg;
var
a, b, c: integer;
begin
write('Ведите число лет, которое было бы Сереже '); readln(a);
b := a + 17;
c := b div 3;
writeln('Сереже было ', c, ' лет')
end.
Если эту программу ввести в компьютер и выполнить, то на экране появится вначале запрос для пользователя:
Введите число лет, которое было бы Сереже
После ввода числа 16, компьютер выдаст на экран:
Сереже было 11 лет
Рассмотрим более детально построение программы.
Она начинается со слова program. Слово program зарезервировано в Паскале, т.е. не может использоваться ни в каких других целях, лишь для начала программы.
После служебного слова program записывается имя программы. В нашей программе именем является serg. Имя программы записывается на английском языке по усмотрению и фантазии автора программы. (В некоторых версиях Паскаля допускается запись имени программы на русском языке).
Конечно, желательным является, чтобы имя программы выражало ее содержание, но как вы сами понимаете, это не всегда возможно.
Имя программы никак в дальнейшем не используется, поэтому требование обязательности объявления имени программы можно считать излишним. Программу можно выполнять и без имени. С другой стороны, - программа без имени неудобна, а иногда непонятна для пользователей и программистов.
Количество символов в имени программы не ограничивается, но значащими считаются первые 63 символа.
Имя программы должно начинаться с буквы. В нем не должно быть пробелов, запятых, точек.
В конце первой строки, после имени программы стоит ";" - точка с запятой.
Этот знак указывает на то, что некоторая инструкция закончена и за ней будет записана следующая инструкция. Правда, первая "инструкция" является именем программы и не походит на инструкцию в смысле "делай то и делай так", но термин " инструкция" мы употребляем в более широком смысле, как одно логически завершенное предложение или его часть. Точка с запятой является обязательным
разделительным знаком в языке Паскаль.
В некоторых версиях языка Паскаль, вы можете встретить такое начало программы:
Program
Serg (input, output);
Как видите, в скобках записаны служебные слова input (ввод) и output (вывод). Они указывают, что в программе будет вводиться и выводиться информация. Для большинства современных версий языка Паскаль и для Турбо Паскаля эти служебные слова являются необязательными. Хотя, надо заметить, их запись в программе не приведет к ошибке. В дальнейшем мы не будем использовать их в программах.
Следующая строка программы:
var
a, b, c : integer;
В этой строке обязательно
указываются все переменные, участвующие в программе и их типы.
Слово var
- это сокращение от слова variable (переменная) и является так же, как и слово program, зарезервированным словом.
После него записываются имена переменных - идентификаторы, в нашем примере: a, b, c. Они записываются через запятую.
После имен переменных стоит ":" - двоеточие, а затем записано служебное, зарезервированное, слово integer. Integer (целый) указывает тип значений, которые принимают переменные - целые числа (..., -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,...). Эта строка программы, также как и предыдущая, заканчивается ";" - точкой с запятой.
Далее в программе следует служебное, зарезервированное, слово begin (начать), которым начинается новый раздел программы - раздел операторов.
В этом разделе последовательно записываются команды, операторы, которые разделяются ";" - точкой с запятой. Они будут выполняться компьютером.
Программа заканчивается
служебным словом end, после которого стоит точка.
Она является обязательной во всех паскалевских программах. Точка оповещает о конце текста программы.
Заметьте, последняя строка из раздела операторов перед служебным словом end не заканчивается точкой с запятой. Но, если вы ее поставите, то ошибки не будет.
1. Итак, КОНСТРУКЦИЯ ПРОГРАММЫ на языке
ПАСКАЛЬ
Program <имя>;
РАЗДЕЛ ОПИСАНИЙ
В нем описываются имена переменных и их типы.
Begin
РАЗДЕЛ ОПЕРАТОРОВ
Ввод данных, последовательность команд, вывод результатов.
end.
Эту конструкцию очень удобно изобразить с помощью блок-схемы. Вспомним, что блок-схема состоит из отдельных геометрических фигур - блоков, каждый из которых показывает какие команды или операции надо выполнить.
Вот эти блоки:

Ввод и выполнение программ

После запуска Турбо Паскаля на экране появится следующая оболочка (см. рис. 3):
Рис. 3
Верхняя строка открывшегося окна содержит "меню" возможных режимов работы Турбо Паскаля, нижняя - краткую справку о назначении основных функциональных клавиш. Вся остальная часть экрана принадлежит окну текстового
редактора, очерченному двойной рамкой и предназначенному для ввода и редактирования текста программы.
Когда мы вводим программу, то работаем с текстовым редактором, встроенным в среду Турбо Паскаль. Поэтому ниже мы и познакомимся с работой редактора и основными его командами.
Признаком того, что среда находится в состоянии редактирования, является наличие в окне редактора курсора - небольшой мигающей черточки.
Для создания текста программы нужно ввести этот текст с помощью клавиатуры подобно тому, как это делается при печатании текста на пишущей машинке. После заполнения очередной строки следует нажать на клавишу <Enter> "Ввод", чтобы перевести курсор на следующую строку (курсор всегда показывает место на экране, куда будет помещен очередной вводимый символ программы).
Окно редактора имитирует длинный и достаточно широкий лист бумаги, часть которого видна в окне экрана. Если курсор достиг нижнего края, осуществляется прокрутка окна редактора: его содержимое смещается вверх на одну строку и внизу появляется новая строка "листа". Наибольшая длина строки на Турбо Паскале - 126 символов.
Окно можно смещать относительно листа с помощью следующих клавиш:
PgUp - на страницу вверх (PaGe UP - страница вверх);
PgDn - на страницу вниз (PaGe DowN - страница вниз);
Home - в начало текущей строки (HOME - домой);
End - в конец текущей строки (END - конец);
Ctrl-PgUp - в начало текста;
Ctrl-PgDn - в конец текста.
Клавишами управления курсора “курсор” можно смещать по тексту на экране (заметьте, только по тексту!).
По "чистому" не исписанному экрану курсор не перемещается!
Если Вы ошиблись при вводе очередного символа, его можно стереть с помощью клавиши, обозначенной стрелкой влево (клавиша Backspace - <Забой>, она располагается справа и вверху зоны основных алфавитно-цифровых клавиш над клавишей <Enter> - “Ввод”). Клавиша <Delete> (Delete - стирать, удалять) стирает символ, на который в данный момент указывает курсор, а команда Ctrl-Y - всю строку, на которой располагается курсор. Следует помнить, что редактор Турбо Паскаля вставляет в конце каждой строки невидимый на экране символ-разделитель. Этот символ вставляется клавишей <Ввод>, а стирается клавишей <Забой> или <Delete>. С помощью вставки/стирания разделителя можно "разрезать”/"склеить" строки.
Чтобы "разрезать" строку, следует подвести курсор к нужному месту и нажать клавишу <Ввод>, чтобы "склеить" соседние строки, нужно установить курсор в конец первой строки и нажать клавишу <Delete>
или установить курсор в начало следующей строки и нажать клавишу <Забой>.
Режим вставки
Нормальный режим работы редактора - режим вставки, в котором каждый вновь вводимый символ как бы "раздвигает" текст на экране, смещая вправо остаток строки. Следует учитывать, что "разрезание" и последующая вставка пропущенных символов возможна только в этом режиме.
Примеры "разрезания", "склеивания" строк и вставки символов в текст.
Пусть по каким-то причинам на экране получена такая запись:
Program Serg; var
a, b, c : integer;
Если говорить об эстетической стороне написания программы, то желательно, чтобы раздел описаний, который начинается со слова var, начинался с красной строки. Для внесения изменений в текст установим курсор на букву v и нажмем клавишу <Ввод>, при этом часть текста после курсора и под ним переместится на следующую строку, получим:
Program Serg;
var
a, b, c : integer;
Для большей красоты и наглядности, не перемещая курсора, а оставляя его на букве v, нажмем несколько раз клавишу <Пробел>. Вся строка передвинется на вправо и запись станет такой:
Program Serg;
var
a, b, c : integer;
Допустим другую ситуацию, когда часть текста "разорвалась" и ее нам надо "склеить", например, получилось так:
write('Введите число лет, кото
рое было бы Серёже ");
Устанавливаем курсор в начало второй строки перед буквой "р" и нажимаем клавишу <Забой>, получим:
write('Введите число лет, которое было бы Серёже ');
Можно поступить иначе, установить курсор в конец первой строки после буквы "о" и нажимая несколько раз клавишу <Delete> "подтягивать" нижнюю строчку вверх.
С помощью клавиш <Забой> и <Delete>
можно "соединять" "разорванную” строку. Например, в такой ситуации:
write('Вве дите число лет, которое было бы Сереже ');
Устанавливаем курсор перед буквой "д" и нажимаем несколько раз клавишу <Забой> до тех пор, пока слово "Введите" примет нужную конструкцию, или, установив курсор после буквы "е" нажать несколько раз клавишу <Delete>.
Вставка пропущенных символов делается еще проще.
Например, вы пропустили несколько букв:
wrte('Ввете число лет, которое было бы Сеже ');
В первом слове пропущена буква "i", в слове "Введите" пропущены две буквы "ди", в слове "Сережа" буквы "ер".
Установим курсор на букву "t" в первом слове и наберем с клавиатуры "i", она тут же вставится на нужное место. Далее установим курсор на букву "т" в слове "Ввете" и наберем с клавиатуры "ди", слово "раздвинется" и буквы "ди" станут на свои места. Установим курсор на "е" в слове "Сежа" и наберем "ер",
Режим наложения
Редактор может также работать в режиме наложения новых символов на существующий старый текст: в этом режиме новый символ заменяет собой тот символ, на который указывает курсор, а остаток строки справа от курсора не смещается вправо. Для перехода к режиму наложения надо нажать клавишу <Insert> (Insert - вставка), если нажать эту клавишу еще раз, вновь восстановится режим вставки. Признаком того, в каком режиме работает редактор, является форма курсора: в режиме вставки курсор похож на мигающий символ подчеркивания, а в режиме наложения он представляет собой крупный мигающий прямоугольник, заслоняющий символ целиком.
Режим автоотступа
Еще одной особенностью редактора является то, что обычно он работает в режиме автоотступа. В этом режиме каждая новая строка начинается в той же позиции экрана, что и предыдущая.
Режим автоотступа поддерживает хороший стиль оформления текстов программ: отступы от левого края выделяют различные операторы и делают программу более наглядной.
Отказаться от режима автоотступа можно командой Ctrl-O I (при нажатой клавише Ctrl
нажимается сначала клавиша O, затем клавиша O отпускается и нажимается клавиша I), повторная команда Ctrl-O I восстановит режим автоотступа.
Ниже перечислены наиболее часто используемые команды текстового редактора Турбо Паскаля, кроме тех, которые были приведены выше.
Команды редактирования
Backspac - <Забой> - стереть символ слева от курсора;
Del - стереть символ, на который указывает курсор;
Ctrl-Y - стереть строку, на которой располагается курсор;
Enter - <Ввод> - вставить новую строку, "разрезать" старую;
Ctrl-Q L - восстановить текущую строку (действует, если
курсор не покидал измененную строку).
Работа с блоком
Ctrl-K B - пометить начало блока;
Ctrl-K Y - стереть блок;
Ctrl-K V - переместить блок;
Ctrl-K R - прочитать блок из дискового файла;
Ctrl-K P - напечатать блок;
Ctrl-K H
- спрятать/отобразить блок (снять пометку);
Ctrl-K K
- пометить конец блока;
Ctrl-K C - копировать блок;
Ctrl-K W
- записать блок в дисковый файл;
Выполнение программы

Для этого нажимаем клавиши <Ctrl>+<F9> (удерживая клавишу <Ctrl>, нажать клавишу <F9>). Эту же операцию можно выполнить, перейдя в основное меню, нажав клавишу <F10>, а затем перемещением указателя выбрать опцию Run и нажать клавишу <Ввода>.
На экране раскроется меню второго уровня, связанное с этой опцией. Новое меню как бы "выпадает" из верхней строки, поэтому такое меню часто называют выпадающим (Pull-down). Экран станет таким (см. рис. 4):
Рис. 4
Теперь надо найти в новом меню опцию RUN (пуск) и нажать клавишу <Ввод>.
Если не было ошибки при вводе текста, то, спустя несколько секунд, произойдет смена изображения на экране. Турбо Паскаль предоставляет экран в распоряжение работающей программы пользователя. Такой экран называется окном программы.
В ответ на запрос:
Введите число лет, которое было бы Серёже, надо ввести 16 и нажать клавишу <Ввод>.
После завершения прогона (работа программы часто называется ее прогоном) на экране вновь появится окно редактора с текстом программы. Если Вы не успели разглядеть изображение окна программы, то нажмите Alt-F5. При этом окно редактора скроется
и вы сможете увидеть результаты работы программы. Чтобы вернуть экран в режим воспроизведения окна редактора, надо нажать на любую клавишу.
Можно экран сделать более удобным, чтобы видеть результаты работы программы. Для этого в нижней части экрана можно открыть второе окно.
Для этого нажмите клавишу F10, чтобы перейти к режиму выбора из главного меню, подведите указатель к опции Debug (отлаживать) и нажмите клавишу <Ввод> - на экране раскроется меню второго уровня, связанное с этой опцией.
Экран станет таким (см. рис. 5):
Рис. 5
Найдите в новом меню опцию OUTPUT (вывод программы), подведите к ней указатель и нажмите клавишу <Ввод>.
В нижней части экрана появится второе окно, но оно уже не будет исчезать.
Теперь добьемся того, чтобы на экране демонстрировалось два окна одновременно: снова нажмите клавишу F10, выберите WINDOW, нажмите клавишу <Ввод>, подведите указатель к опции TILE (черепица) и нажмите клавишу <Ввод>.
Если все сделано правильно, экран примет вид (см. рис. 6):
Рис. 6
Двойная рамка, очерчивающая окно программы, свидетельствует о том, что именно это окно активно в данный момент.
Сделаем активным окно редактора: нажмем клавишу <Alt> и, не отпуская ее, - клавишу с цифрой 1 (окно редактора имеет номер 1, окно программы - номер 2, эти номера написаны в верхних правых углах рамок). Теперь всё готово к дальнейшей работе с программой.
Первые ошибки и их исправление
1. Не поставлена точка с запятой, например, после оператора readln(a). После пуска программы, нажатием клавиш <Ctrl>+<F9>, в верхней строке экрана появится написанное красным цветом сообщение:
Error 85: ";" expected.
(Ошибка 85: ";" отсутствует.)
Редактор установит курсор на следующий символ после пропущенного знака, в нашем примере на переменную b. После нажатия любой клавиши, сообщение об ошибке исчезает и редактор переходит в режим вставки. Надо подвести курсор к нужному месту, поставить точку с запятой - “;” и продолжить работу.
2. В описании переменных не записана переменная, а в программе она присутствует, например переменная c. После пуска программы, будет выдано сообщение:
Error 3: Unknown identifier.
(Ошибка 3: Неизвестный идентификатор.)
Курсор будет установлен на эту переменную, в нашем примере на переменную c. Надо исправить ошибку, т.е. записать переменную c в раздел описаний переменных и продолжить работу.
3. Не поставлена точка после оператора end в конце программы.
Сообщение компилятора будет таким:
Error 10: Unexpected end of file.
(Ошибка 10: Неправильный конец файла.),
курсор установится на букву "e" в слове "end". Надо поставить точку и снова выполнить программу.
Запись файла на диск
Итак, программа отредактирована и выполнена (прокручена), теперь ее надо записать на диск. Для этого можно воспользоваться основным меню, в котором выбрать опцию "File" (см. рис. 7). Последовательность действий такова: 1) нажать клавишу F10 и перейти в основное меню; 2) переместить указатель на опцию "File" и нажать <Ввод>, откроется второе меню опции "File":
Рис. 7
Вы можете из этого меню выбрать опцию "Save". Она записывает содержимое активного окна редактора в дисковый файл.
Если нажать клавишу <Ввод>, то среда запросит имя файла, если такового не было установлено и окно было связано с именем NONAME00.PAS. Вы можете изменить имя, или оставить его прежним.
Эта опция вызывается непосредственно из редактора клавишей <F2>.
Можно выбрать опцию SAVE AS. Она записывает содержимое активного окна редактора в дисковый файл под другим именем.
Диалоговое окно этой опции имеет вид (см. рис. 8):
Рис. 8
В поле ввода Вы должны написать имя того файла, в который будет переписано содержимое активного окна редактора. Вы можете выбрать уже существующий файл из поля выбора или из протокола с опциями. В этом случае в зависимости от настройки среды старое содержимое файла будет уничтожено или сохранено в виде страховой копии с расширением .BAK.
Построчная запись текста программы
В Паскале нет правил разбивки текста программы на строки.
Однако для записи программы можно дать некоторые
Рекомендации
Очень важно, чтобы текст программы был расположен наглядно не только ради красоты, но (и это главное!) ради избежания ошибок. (Найти ошибки в наглядном тексте значительно легче.)
1. Каждый оператор следует писать с новой строки, за исключением коротких и по смыслу связанных операторов.
Например,
write ... readln ... - записываются в одной строке, короткие операторы присваивания можно записать в одну строку:
a := 23; b := 105; c := -11.2.
2. Операторы одного уровня, находящиеся в разных строках, должны быть выровнены по вертикали, т.е. одинаково отодвинуты от левого края.
Например, запишем последовательность операторов для определения суммы цифр трехзначного числа:
s := a div 100;
d := a div 10 mod 10;
e := a mod 10;
sum := s + d + e
Здесь все операторы равноценны, последовательно идут один за другим, поэтому все начинаются с одной и той же вертикальной позиции.
3. Операторы, включенные в другой оператор, следует сдвинуть вправо на несколько позиций (желательно одинаково).
begin
write ...
readln ...
if ... then
begin
.....
end
else
begin
.....
end;
end.
4. Рекомендуется вертикально выравнивать пары базовых слов: begin и end, с которыми мы уже познакомились, а также слова, с которыми мы познакомимся позже: repeat и until, record и end, case
и end.
5. Оператор if рекомендуется размещать с учетом длины и сложности условия, и операторов, идущих после слов then и else.
Вот несколько самых популярных вариантов размещения оператора if:
а) if ... then ...
else ...
б) if ... then ...
else ...
в) if ...
then ...
else ...
г) if ...
then ...
else ...
д) if ... then ... else ...
6. Комментарии пишутся либо рядом с конструкцией (идентификатором, оператором, его частью), которую они объясняют, либо в отдельной строке.
7. После знаков препинания: , - запятой, ; - точки с запятой, : - двоеточия рекомендуется оставлять по одному пробелу.
Задание
Наберите программу Serg и выполните ее.Закончите работу в системе Turbo Pascal.
Интегральная формула Муавра-Лапласа
Если вероятность p наступления события в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, в n независимых испытаниях событие состоится число раз, заключенное в границах от [m1; m2] (m1 < m2), приближенно равна:

где

а

Для применения этой формулы, необходимо составить функцию вычисления интеграла

Для его вычисления воспользуемся способом разложения подынтегральной функции в ряд с последующим интегрированием членов полученного степенного ряда с заданной степенью точности. (Подробнее об этом см. в главе "Числовые и функциональные ряды", "Приближенное вычисление интегралов с помощью рядов").
При составлении функции учтем то обстоятельство, что при


В результате получим следующую функцию для вычисления интегральной функции Муавра-Лаплапса:
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if
x >= 5
then FF := 1
else if x <= -5
then
FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)) )
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
Используя эту функцию, составим процедуру для вычисления вероятности появления события из заданного интервала [m1; m2].
{ Процедура вычисл. вероятн. наст. событ. из промеж. [m1; m2] }
Procedure Interval(n, m1, m2 : longint; p : real; var PP : real);
var
x1, x2 : real;
begin
x1 := (m1 - n*p)/sqrt(n*p*(1 - p));
x2 := (m2 - n*p)/sqrt(n*p*(1 - p));
PP := (FF(x2) - FF(x1))/2
end;
Дальнейшее не представляет труда. Полученные функция и процедура дают нам возможность решать довольной большой круг задач определения вероятности наступления событий. Разберем это на конкретных примерах.
Пример 1. Вероятность некоторого события равна 0.4 в каждом из n испытаний. Найти вероятность того, что число появления события при n = 1500 будет заключено между 1) 570 и 630; 2) 600 и 660; 3) 620 и 680; 4) 580 и 640.
Программа
{ Применение интегральной формулы Муавра-Лапласа }
Program Problem1;
uses WinCrt;
var
n, m1, m2 : longint;
p, PP : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer; u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисл. вероятн. наст. событ. из промеж. [m1; m2] }
Procedure Interval(n, m1, m2 : longint; p : real; var PP : real);
var
x1, x2 : real;
begin
x1 := (m1 - n*p)/sqrt(n*p*(1 - p));
x2 := (m2 - n*p)/sqrt(n*p*(1 - p));
PP := (FF(x2) - FF(x1))/2
end;
{----------------------------------------------------------------------------------------}
{ Основная программа. Число бракованных изделий из промежутка }
begin
write('Введите общее число изделий '); readln(n);
write('Введите вероятность наступление одного события '); readln(p);
write('Введите левую границу промежутка '); readln(m1);
write('Введите правую границу промежутка '); readln(m2);
Interval(n, m1, m2, p, PP);
writeln('Вероятность того, что число бракованных изделий');
write('находится в промежутке [',m1, '; ', m2, '] равна ');
writeln(PP:1:8)
end.
Пример 2. Число отклонений от установленного стандарта при обточке металлических болванок составляет, по данным длительной проверки ОТК, 0.12 от взятого количества продукции. Определить вероятность того, что из взятых наудачу 25 образцов не менее 21 будет соответствовать стандарту.
Программа
{ Применение интегральной формулы Муавра-Лапласа }
Program Problem2;
uses WinCrt;
var
n : longint;
e, p, PP : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления вероятности частоты наступления событий }
{ при заданной точности e }
Procedure Probability(n : longint; p, e : real; var PP : real);
var
x : real;
begin
x := e/sqrt(n*p*(1 - p));
PP := FF(x)
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write(' Введите вероятность приема одного сообщения ');
write('без ошибок '); readln(p);
write('Введите общее число сообщений '); readln(n);
writeln('На сколько число принятых сообщений должно быть');
write('безошибочным, (точность) прин. сообщ. '); readln(e);
Probability(n, p, e, PP);
writeln('Искомая вероятность равна ', PP:1:8)
end.
Пример 3. На склад поступает продукция трех фабрик, причем изделия первой фабрики на складе составляют 30%, второй - 32% и третьей - 38%. В продукции первой фабрики 60% изделий высшего сорта, второй - 25%, третьей - 50%. Найти вероятность того, что среди 300 наудачу взятых со склада изделий число изделий высшего сорта заключено между 130 и 170.
В этой задаче прежде надо определить вероятность получения числа изделий высшего сорта со всех трех фабрик, т.е. их наличие на складе.
Пусть H1 - изделие сделано на 1-ой фабрике, P(H1) = 0.3; H2
- изделие сделано на 2-ой фабрике, P(H2) = 0.32; H3 - изделие сделано на 3-ей фабрике, P(H3) = 0.38.
A - изделие высшего сорта. В задаче даны PHi(A), i = 1, 2, 3;

{ Применение интегральной формулы Муавра-Лапласа }
Program Problem3;
uses WinCrt;
var
n, m1, m2 : longint;
p, PP : real;
{----------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисл. вероятн. наст. событ. из промеж. [m1; m2] }
Procedure
Interval(n, m1, m2 : longint; p : real; var PP : real);
var
x1, x2 : real;
begin
x1 := (m1 - n*p)/sqrt(n*p*(1 - p));
x2 := (m2 - n*p)/sqrt(n*p*(1 - p));
PP := (FF(x2) - FF(x1))/2
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите общее число изделий '); readln(n);
p := 0.6*0.3 + 0.25*0.32 + 0.5*0.38;
write('Введите левую границу промежутка '); readln(m1);
write('Введите правую границу промежутка '); readln(m2);
Interval(n, m1, m2, p, PP);
writeln('Вероятность того, что число изделий высшего');
write('сорта находится в [',m1, '; ', m2, '] равна '); writeln(PP:1:8)
end.
Классические методы нахождения изолированного корня
На этом занятии мы рассмотрим задачу нахождения корней уравнения
f(x) = 0. (1)
"Изолированным" мы будем называть корень c уравнения (1), если найден, содержащий его промежуток [a, b]: a < c < b, на котором других корней нет.
Для решения задачи уточнения корня, потребуем, чтобы функция удовлетворяла следующим условиям:
1) f(x), f'(x) и f''(x) непрерывны на промежутке [a, b]; 2) значения функции на концах промежутка [a, b] имеют разные знаки:

3) обе производные f'(x) и f''(x) сохраняют каждая определенные знаки на всем промежутке [a, b], это значит, что функция строго монотонна (возрастает или убывает) на этом промежутке. Требование сохранение знака второй производной f''(x) геометрически означает, что график функции вогнутостью обращен всегда в одну сторону и не имеет перегибов.
Столь жесткие требования к поведению функции на промежутке казалось бы сильно сужают круг рассматриваемых функций, но это не так.
Для алгебраических функций всегда можно найти промежуток (если вообще вещественные корни алгебраического уравнения существуют), на котором все три перечисленных условия выполняются.
Что касается трансцендентных уравнений, то на практике в большинстве случаев перечисленные условия выполняются и для них.
Во всяком случае, круг уравнений достаточно широк, чтобы заняться рассмотрением ниже приводимых приемов решения, тем более что эти способы являются классическими и полезны будут даже из соображений общего развития читателей.
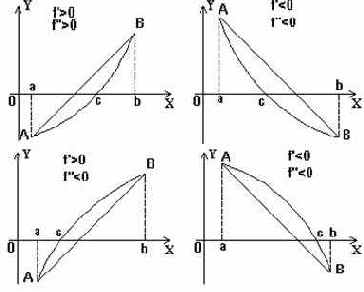
Рис. 44
На рисунке 44 изображены четыре возможные случая, отвечающие различным комбинациям знаков f'(x) и f''(x).
1-й случай, когда f'(x)>0 - функция возрастает на промежутке, f''(x) > 0 - график вогнутостью направлен вверх.
2-й случай: f'(x)<0 - функция убывает, f''(x)>0 - вогнутость вверх.
3-й случай: f'(x) > 0 - функция возрастает, f''(x) < 0 - вогнутость направлена вниз.
4-й случай: f'(x) < 0 - функция убывает, f''(x) < 0 - вогнутость вниз.
1.1. Метод хорд (правило пропорциональных частей)
Пусть c - корень уравнения f(x) = 0 на промежутке [a, b], тогда c - абсцисса точки пересечения кривой с осью ox. Конечная задача - найти эту точку или как можно близкое значение абсциссы к этой точки.
Рассмотрим случаи 1-й и 3-й, когда хорда находится слева от кривой и пересекает ось x между точками a и c (см. рис. 45).
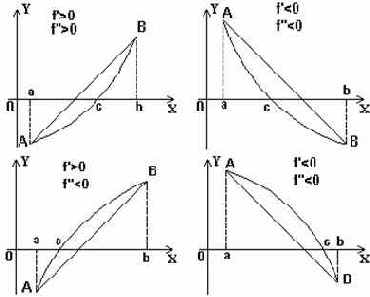
Рис. 45
Заменим кривую AcB хордой AB. Мы сможем написать уравнение этой хорды, а значит найти ее точку пересечения с осью x.
Уравнение хорды - это уравнение прямой, проходящей через две точки (a, f(a)) и (b, f(b)).
Общий вид уравнения прямой, проходящей через две точки такой:

Подставляя в эту формулу значения, получим уравнение хорды AB:


Пусть x1
- точка пересечения хорды с осью x, так как y = 0, то

x1 может считаться приближенным значением корня. Для более точного его определения рассмотрим промежуток [x1, b]. И на этом промежутке заменим кривую хордой A1B и найдем новое приближение к корню - x2:

Для n + 1 - го приближения получим:

Этот процесс можно продолжать сколь угодно долго и построить возрастающую последовательность приближенных значений корня:
a < x1
< x2 < ... < xn < xn+1 < ... < c.
В математическом анализе доказывается, что переменная xn с ростом n стремится к c, т.е. c является пределом этой последовательности.
Для случаев 2-го и 3-го, когда хорда располагается справа от кривой (см. рис. 46), и пересекает ось ox между точками с и b, значения приближенных значений корней будут следующими:
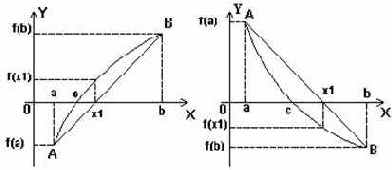
Рис. 46


....................................,

В результате получим убывающую последовательность, которая также сходится к c:
b > x1
> x2 > ... > xn > xn+1 > ... > c
Во всех случаях можно найти корень с любой степенью точности.
Как оценивается точность приближенного значения xn?
По формуле Лагранжа (формуле конечных приращений) для разности




Так как f(c) = 0, то получим:

Если обозначить через m наименьшее значение |f'(x)| на промежутке [a, b], которое можно определить заранее, то получим формулу для оценки точности вычисления корня:


где eps - заданная точность вычисления. Пользуясь рекуррентной формулой (1) и формулой для оценки точности вычисления, нетрудно составить процедуру уточнения корня методом хорд:
{ Процедура уточнения корня методом хорд }
Procedure chord(a, b, eps, min : real; var
x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - ((b - x1)*fx(x1))/(fx(b) - fx(x1));
x1 := x
until abs(fx(x))/min < eps
end;
Для оценки точности вычисления корня необходимо вычислять наименьшее значение производной f'(x) на промежутке [a, b], поэтому возникает необходимость в нахождении значения производной в точке и здесь мы приходим к задаче численного дифференцирования.
1.2. Вычисление производных (численное дифференцирование)
При вычислении производной функции, будем иметь в виду, что один из способов найти производную



Таким образом, вычисляется производная в середине промежутка.
По значениям f' можно таким же способом найти производную от f', т.е. f''. Можно выразить f'' непосредственно через f(x):


Для производной третьего порядка можно использовать следующую формулу:

Возникают естественные вопросы, откуда происходят эти формулы и как оценивать точность вычисления производных по этим формулам?
Формулы являются результатом дифференцирования интерполяционных многочленов Ньютона и других. Сущность которых состоит в том, что заданная функция f(x) представляется в виде многочлена, который значительно проще дифференцировать, чем какие-либо другие функции, особенно трансцендентные или представляющие собой сложные выражения. Как получаются такие многочлены, мы узнаем позже - этому вопросу будет посвящена полностью глава, а сейчас ограничимся лишь результатами, которые нам необходимы в этой главе.
Оценка погрешности и точности вычисления не менее серьезный и сложный процесс, чем само приближенное вычисление.
Так для оценки погрешности дифференцирования могут быть применены следующие формулы:

где предполагается, что функция f(x) дифференцируемая n + 1 раз, а точка

На практике f
(n+1)(c) оценивать непросто, поэтому при малых dx приближенно полагают:

и тогда получается следующая формула

Мы будем пользоваться формулой (2), а впоследствии и формулой (3), в зависимости от конкретной задачи и тех сложностей, которые могут возникнуть при составлении программ.
Используя эти формулы, составим функцию для вычисления первой производной. Точность вычисления eps задается пользователем, а первоначальная величина промежутка dx устанавливается 1, а затем, для уточнения вычисления - делится на 2. Впрочем, читатель может предложить другие способы изменения промежутка dx, когда значительно быстрее достигается вычисление производной с заданной степенью точности.
{ Вычисление 1-й производной и опред. точности ее вычислен.}
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs(dy2/(2*dx)) < eps;
derivat1 := dy/dx
end;
Здесь, для определения точности вычисления, используется вторая производная в точке

Запись ее вычисления выполнена в две строки только из-за лучшей наглядности написания программы.
Возможен и другой вариант написания функции с использованием формулы (3) для оценки точности вычисления.
Тогда функция запишется так:
{ Вычисление 1-й производной и опред. точности ее вычислен.}
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs((dy2*dy2*fx(x0))/(2*dx)) < eps;
derivat1 := dy/dx
end;
Задание 1
Составьте самостоятельно функции для вычисления второй производной и проверьте ее работу в программах для вычисления второй производной функций:

Однако вернемся к задаче решения уравнения методом хорд. Имея возможность вычислить значение производной, можно составить процедуру определения модуля ее наименьшего значения на промежутке [a, b].
Для этого достаточно сравнить модуль значения производной на концах промежутка и выбрать среди этих двух значений меньшее (такое право дает нам сделать тот факт, что по условию, функция на промежутке строго монотонна вместе со своими производными первого и второго порядков). Процедура получится простой:
{ Процедура определения наименьшего значения производной }
Procedure
minimum(a, b, eps : real; var min : real);
begin
min := abs(derivat1(a, eps));
if min > abs(derivat1(b, eps))
then min := abs(derivat1(b, eps))
end;
Но и построенная таким образом процедура имеет очень существенный недостаток! А если в точке a или b производная будет равна нулю? Тогда деление на нуль станет невозможным и в программе будет получена ошибка. Чтобы избежать этого, изменим процедуру так, чтобы в случае равенства нулю производной в одной и точек a или b находилось бы ее значение в ближайшей окрестности этой точки. Но, для точки a брать значение слева нельзя, оно выйдет за пределы промежутка [a, b], также, как и справа от точки b. Поэтому следует брать значение очень близкое к a, но справа от нее, аналогично для точки b - брать близкое значение слева от b.
Процедуру
можно построить так:
{ Процедура определения наименьшего значения производной }
{ на заданном промежутке }
Procedure minimum(a, b, eps : real; var min : real);
var
d : real;
begin
a := a - eps;
b := b + eps;
repeat
a := a + eps;
b := b - eps;
min := abs(derivat1(a, eps));
d := abs(derivat1(b, eps));
if min > d then min := d
until min <> 0
end;
Объединяя полученные функции и процедуры в одну программу, мы получим программу вычисления корня уравнения на изолированном промежутке методом хорд.
{ Решение уравнений методом хорд. method - метод, chord - хорда }
Program Method_Chord;
uses WinCrt;
var
a, b, x, min, eps : real;
{--------------------------------------------------------------------------------------}
{ Заданная функция }
Function fx(x : real) : real;
begin
fx := x*x*x - 2*x*x - 4*x - 7
end;
{--------------------------------------------------------------------------------------}
{ Вычисление 1-й производной }
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs(dy2/(2*dx)) < eps;
derivat1 := dy/dx
end;
{----------------------------------------------------------------------------------------}
{ Процедура определения наименьшего значения производной }
{ на заданном промежутке }
Procedure minimum(a, b, eps : real; var min : real);
var
d : real;
begin
a := a - eps;
b := b + eps;
repeat
a := a + eps;
b := b - eps;
min := abs(derivat1(a, eps));
d := abs(derivat1(b, eps));
if min > d then min := d
until min <> 0
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом хорд }
Procedure chord(a, b, eps, min : real; var
x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - ((b - x1)*fx(x1))/(fx(b) - fx(x1));
x1 := x
until abs(fx(x))/min < eps
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите левый конец промежутка a = '); readln(a);
write('Введите правый конец промежутка b = '); readln(b);
write('Введите точность вычисления корня eps = ');
readln(eps);
minimum(a, b, eps, min);
chord(a, b, eps, min, x);
writeln('Корень уравнения равен x = ', x:12:12);
writeln('С точностью до eps = ', eps:1:12)
end.
И в этих программах будем применять уже известную нам функцию для указания точности вычисления.
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
Добавим эту функцию в программу.
{ Решение уравнений методом хорд. method - метод, chord - хорда}
{ Правило пропорциональных частей }
Program
Method_Chord;
uses WinCrt;
var
a, b, x, min, eps : real;
{----------------------------------------------------------------------------------------}
{ Заданная функция }
Function fx(x : real) : real;
begin
fx := x*x*x - 2*x*x - 4*x - 7
end;
{----------------------------------------------------------------------------------------}
{ Вычисление 1-й производной }
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs(dy2/(2*dx)) < eps;
derivat1 := dy/dx
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Процедура определения наименьшего значения производной }
{ на заданном промежутке }
Procedure minimum(a, b, eps : real; var min : real);
var
d : real;
begin
a := a - eps;
b := b + eps;
repeat
a := a + eps;
b := b - eps;
min := abs(derivat1(a, eps));
d := abs(derivat1(b, eps));
if min > d then min := d
until min <> 0
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом хорд }
Procedure chord(a, b, eps, min : real; var
x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - ((b - x1)*fx(x1))/(fx(b) - fx(x1));
x1 := x
until abs(fx(x))/min < eps
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите левый конец промежутка a = '); readln(a);
write('Введите правый конец промежутка b = '); readln(b);
write(' Введите точность вычисления корня eps = ');
readln(eps);
minimum(a, b, eps, min);
chord(a, b, eps, min, x);
writeln('Корень уравнения равен x = ', x:6:t(eps));
writeln('С точностью до eps = ', eps:1:t(eps))
end.
1.3. Правило Ньютона (метод касательных)
Будем по прежнему считать, что функция f(x) удовлетворяет всем перечисленным ранее требованиям и искомый корень c изолирован на промежутке [a, b], т. е. a < c < b.
Если в предыдущем примере была предпринята замена кривой, - графика функции, хордой, то возникает естественная идея, а почему бы не заменить ее касательной, проведенной первоначально из точек A или B.
Этот метод носит название правило Ньютона или метод касательных.
Также возможны четыре случая, которые представлены на рисунке 47.
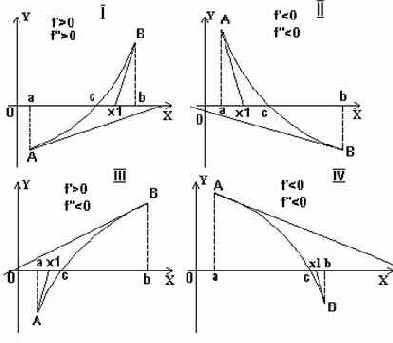
Рис. 47
Рассмотрим уравнение касательной, проведенной в точке B с абсциссой b. Уравнение касательной в этой точке составить нетрудно, оно будет таким:

зная, что в точке пересечения с осью ox y = 0, найдем из уравнения значение x, получим:

Таким образом, мы получаем приближенное значение корня

Возникает вопрос, где лежит точка x1, полученная по формуле (3). Ведь из рисунка следует, что в случаях 2 и 3 она может лежать вообще за пределами промежутка.
В математическом анализе доказывается, что если значение f(b) одного знака с f''(x) - это случаи 1 и 4, то x1 лежит между корнем c и точкой b.
Аналогично, если исходить из точки a, и касательную к кривой провести в точке A, то получим следующую формулу для приближенного значения корня

Также и здесь доказывается, что если f(a) и f''(a) одного знака, то x1 лежит между a и c, a < x1 < c (на рисунке это соответствует случаям 2 и 3).
Как и для случая метода хорд можно построить для 1-го и 4-го случаев убывающую последовательность значений xn сходящейся к c:
b > x1
> x2 > ... > xn > xn+1 > ... > c,
а для случаев 2 и 3 возрастающую последовательность значений также сходящихся к c: a < x1 < x2
< ... < xn < xn+1 < ... < c.
Вычисление значений членов последовательности производится по следующей рекуррентной формуле:

Надо иметь ввиду, что для выбора первоначального значения x (x = a или x = b), надо установить, где знак функции f(x) совпадает со знаком f''(x).
Оценка точности приближения происходит также, как и для случая метода хорд по значению отношения

Исходя из высказанных соображений составим процедуру уточнения корня методом касательных.
{ Процедура уточнения корня методом касательных }
Procedure tangent(a, b, eps, min, dy : real; var x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - fx(x1)/derivat1(x1);
x1 := x
until abs(fx(x))/min < eps
end;
Для установления первоначального значения x (конца промежутка, от которого начнется уточнения корня) нам нужна будет вторая производная. Функцию, которая ее вычисляет вы должны были составить самостоятельно, а сейчас проверьте себя:
{ Функция вычисления второй производной }
Function
derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
Программа
{ Решение уравнений методом касательных. method - метод }
{ tangent - касательная. Правило пропорциональных частей }
Program Method_Tangent;
uses WinCrt;
var
a, b, x, min, eps : real;
{----------------------------------------------------------------------------------------}
{ Заданная функция }
Function fx(x : real) : real;
begin
fx := x*x*x - 2*x*x - 4*x - 7
end;
{----------------------------------------------------------------------------------------}
{ Вычисление 1-й производной }
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs((dy2*dy2*fx(x0))/(2*dx)) < eps;
derivat1 := dy/dx
end;
{----------------------------------------------------------------------------------------}
Function derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Процедура определения наименьшего значения производной }
{ на заданном промежутке }
Procedure minimum(a, b, eps : real; var min : real);
var
d : real;
begin
a := a - eps;
b := b + eps;
repeat
a := a + eps;
b := b - eps;
min := abs(derivat1(a, eps));
d := abs(derivat1(b, eps));
if min > d then min := d
until min <> 0
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом касательных }
Procedure tangent(a, b, eps, min : real; var x : real);
var
x1 : real;
begin
x1 := a;
repeat
x := x1 - fx(x1)/derivat1(x1, eps);
x1 := x
until abs(fx(x))/min < eps
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите левый конец промежутка a = '); readln(a);
write('Введите правый конец промежутка b = ');
readln(b);
write('Введите точность вычисления корня eps = ');
readln(eps);
minimum(a, b, eps, min);
if fx(a)*derivat2(a, eps) > 0
then tangent(a, b, eps, min, x)
else tangent(b, a, eps, min, x);
writeln('Корень уравнения равен x = ', x:6:t(eps));
writeln('С точностью до eps = ', eps:1:t(eps))
end.
Вы обратили внимание, что первая производная вычисляется с определением точности вторым способом через приращение аргумента и приращение функции. Почему это сделано?
Когда выяснялся вопрос о точности вычисления производных, то оговаривалось, что при оценки погрешности первой производной по значению второй производной, точка, в которой вычисляется значение второй производной должна быть отлична от x0 и от точек, которые отстоят от x0 на расстоянии кратном dx. При вычислении корня по методу касательных значение первой производной меняется в зависимости от x1, которое может неожиданно попасть в точку, отстоящую от x0 на расстоянии кратном dx, что недопустимо. Поэтому оценка погрешности выполняется вторым способом.
1.4. Комбинированный метод касательных и хорд
Он состоит в одновременном использовании как метода касательных, так и метода хорд.
Если Вы внимательно следили за вычислениями приближенных значений двумя методами, то вероятно заметили, что если методом хорд последовательность значений, начиная от первоначального значения a - левого конца промежутка, возрастает, то для этого же случая по методу касательных последовательность убывает.
Для других двух случаев получается наоборот. Таким образом, получаемые последовательности сближаются и тем самым, применяя одновременно два метода можно получить более быстрое приближение корня.
Если мы имеем дело со случаем 1, тогда, обозначая приближенные значения по методу хорд x1, а по методу касательных - z1, получим:


тогда, a < x1 < c < z1 < b.
При следующем шаге заменяется в этих формулах a и b через x1 и z1:


Общие формулу для построения приближений будут следующими:


О качестве достигнутого приближения, т.е. о точности, можно судить по величине |zn
- xn| - в этом удобство комбинированного метода.
Необходимо изменить процедуры вычисления приближенных корней уравнения по методу хорд и методу касательных следующим образом:
{ Процедура уточнения корня методом хорд }
Procedure chord(a, b : real; var
x : real);
begin
x := a - ((b - a)*fx(a))/(fx(b) - fx(a))
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом касательных }
Procedure tangent(a, b, eps : real; var
z : real);
begin
z := a - fx(a)/derivat1(a, eps)
end;
В основной программе организовать цикл до выполнения условия

{ Решение уравнений комбинированным методом хорд и касательных }
Program Combination_Method;
uses WinCrt;
var
a, b, x, z, eps : real;
{----------------------------------------------------------------------------------------}
{ Заданная функция }
Function fx(x : real) : real;
begin
fx := x*sin(x) - 0.5
end;
{----------------------------------------------------------------------------------------}
{ Вычисление 1-й производной }
{ derivative - производная }
Function derivat1(x0, eps : real) : real;
var
dx, dy, dy2 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx/2) - fx(x0 - dx/2);
dy2 := fx(5*x0/4 + dx) - 2*fx(5*x0/4);
dy2 := dy2 + fx(5*x0/4 - dx)
until abs((dy2*dy2*fx(x0))/(2*dx)) < eps;
derivat1 := dy/dx
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления второй производной }
Function derivat2(x0, eps : real) : real;
var
dx, dy, dy3 : real;
begin
dx := 1;
repeat
dx := dx/2;
dy := fx(x0 + dx) - 2*fx(x0) + fx(x0 - dx);
dy3 := fx(5*x0/4 + 2*dx) - 2*fx(5*x0/4 + dx);
dy3 := dy3 - fx(5*x0/4 - 2*dx) + 2*fx(5*x0/4 - dx)
until abs(dy3/(6*dx)) < eps;
derivat2 := dy/(dx*dx)
end;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом хорд }
Procedure chord(a, b : real; var
x : real);
begin
x := a - ((b - a)*fx(a))/(fx(b) - fx(a))
end;
{----------------------------------------------------------------------------------------}
{ Процедура уточнения корня методом касательных }
Procedure tangent(a, b, eps : real; var
z : real);
begin
z := a - fx(a)/derivat1(a, eps)
end;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите левый конец промежутка a = '); readln(a);
write('Введите правый конец промежутка b = '); readln(b);
write(' Введите точность вычисления корня eps = ');
readln(eps);
repeat
if fx(a)*derivat2(a, eps) > 0
then
begin
tangent(a, b, eps, z);
chord(b, a, x);
b := z; a := x
end
else
begin
tangent(b, a, eps, z);
chord(a, b, x);
b := x; a := z
end
until abs(z - x) < eps;
writeln('Корень уравнения равен x = ', x:6:t(eps));
writeln('С точностью до eps = ', eps:1:t(eps))
end.
Задание 2
При выполнении задания Вам необходимо использовать программу отделения корней, которая изучалась ранее. Таким образом, задания надо выполнять в таком порядке:
1) графическим путем найти самый "большой" промежуток, на котором может находится один или более корней (это можно сделать "вручную", схематически вычертив графики функции);
2) составить программу, в которой объединяется метод отделения корней (другими словами, нахождение изолированных промежутков) и соответствующий метод уточнения корня (метод хорд, касательных или комбинированный).
1. При решении следующих уравнений используйте для уточнения корня метод хорд:

2. Примените для уточнения корня метод касательных:

Замечание. Последнее уравнение можно преобразовать к виду более удобному для решения: ln(3x ) = ln(3x) или xln3 = ln(3x), xln3 - ln(3x) = 0.
Вообще для вычисления степени ax с любым действительным показателем и любым положительным действительным основанием можно составить отдельную процедуру, основываясь на следующих соображениях:
ax = y, ln(a x) = lny, xlna = lny, y = e xlna, окончательно получаем a = exlnx .
На Паскале это запишется так: exp(x*ln(a)).
3. Для решения следующих уравнений используйте в качестве метода уточнения корней, комбинированный метод:

Классическое определение вероятности
Самый удобный инструмент для первого знакомства с вероятностями - игральная кость: кубик, грани которого занумерованы числами 1, 2, ..., 6.
Поскольку кубик совершенно симметричен, мы считаем, что все шесть исходов бросания кости, т.е. выпадения цифр 1 или 2, или 3, или 4, или 5, или 6 имеют совершенно одинаковую возможность.
Если отвлечься от реального содержания исходов испытания и интересоваться лишь тем, произошел или не произошел тот или иной исход, мы получим понятие элементарного события, которое в теории вероятностей является основным и не определяется.
В теории вероятностей под событием мы будем понимать все то, что может произойти, но может и не произойти в результате выполнения некоторой совокупности (комплекса) условий. Такие события называются случайными событиями.
Например, случайными событиями будут:
а) попадание в цель при выстреле;
б) выпадение орла при бросании монеты;
в) наудачу взятое изделие - стандартное;
г) наудачу взятое изделие - бракованное;
д) выпадение определенного числа очков при бросании игральной кости и т.д.
Условимся события обозначать большими буквами латинского алфавита A, B, C, ... и т. д. В дальнейшем, если данный комплекс условий многократно повторяется, мы вместо слов "совокупность условий выполнена" будем говорить: "произведено испытание" или "произведен опыт". Другими словами, событие
мы будем рассматривать как результат испытания.
Так в примере а) выстрел - это испытание, а попадание в цель - это событие; в примере б) подбрасывание монеты - это испытание, а выпадение орла - это событие и т. д.
Условимся буквой P обозначать вероятность события, и сформулируем определение вероятности события.
Рассмотрим следующий пример. В урне содержится девять одинаковых, тщательно перемешанных между собой шаров, причем четыре из них - красных, три - синие и два - белые.
Поставлена задача: найти количественную оценку того, что взятый наудачу шар будет цветным. Каждый из возможных результатов испытания (извлечение шара из урны) будем называть элементарным исходом.
В нашем примере возможны девять элементарных исходов: C1, C2 - появился белый шар, C3, C4, C5 - появился синий шар, C6, C7, C8, C9 - появился красный шар.
Элементарные исходы, при которых событие наступает, называются благоприятствующими
исходами.
В нашем примере событию: "взятый шар цветной", благоприятствуют следующие исходы: C3, C4, C5, C6, C7, C8, C9. Поэтому вероятность того, что взятый шар окажется цветным, равна P=7/9.
Вероятностью события A называется отношение числа событий, благоприятствующих событию A (m), к общему числу всех равновозможных событий (n), т. е.


Из определения вероятности вытекают следующие ее свойства:
1. Наибольшую вероятность имеет достоверное событие, т.к. для него все элементарные исходы - благоприятствующие, т. е. P = 1.
2. Наименьшую вероятность имеет невозможное событие - P = 0.
3. Вероятность любого случайного события удовлетворяет неравенству:
0 < P < 1.
Рассмотрим примеры, для решения которых используется вероятность событий. Нас будет интересовать применение комбинаторики к вычислению вероятностей.
Вот несколько примеров вычисления вероятностей с помощью сочетаний, размещений и перестановок.
Пример 1. Пусть мешок содержит одинаковые по размерам и материалу шары, помеченные числами от 1 до 90. Из мешка вытаскивают какие-то 5 шаров. Какова вероятность, что среди этих шаров один помечен числом 90?
Вначале приведем математическое решение задачи, затем составим алгоритм и программу на языке Паскаль, т.е. будем придерживаться традиционной схемы решения задач на компьютере:
математическая модель - алгоритм - программа - отладка.
Событием в этой задаче является извлечение пятерки шаров (например, попали пять шаров с числами 24, 35, 42, 64, 83).
Каждая такая пятерка является подмножеством из множества 90 элементов, поэтому число таких подмножеств равно числу сочетаний из 90 элементов по 5:


Какое число событий будет благоприятствовать появлению шара с номером 90?
Допустим, что шар с номером 90 извлечен из мешка, тогда в мешке останется 89 шаров, из которых извлекаются еще 4 шара в добавление к одному с номером 90.
Извлечь 4 шара из 89 можно


Искомая вероятность будет равна:

Алгоритм
1. Содержание:
а) имя программы;
б) описание переменных и их типов;
в) описание процедуры вычисления числа сочетаний.
2. Выполнение операторов:
а) вызов процедуры сочетаний и вычисление числа сочетаний из 90 по 5;
б) вызов процедуры сочетаний и вычисление числа сочетаний из 89 по 4;
в) вычисление вероятности; г) вывод результата.
3. Конец.
По алгоритму составим программу, используя процедуру вычисления числа сочетаний.
Программа
Program Problem1;
uses WinCrt;
var
n1, m : longint;
p : real;
{----------------------------------------------------------------------------------------}
Procedure combination(n, k : integer; var s : longint);
var
i : longint;
begin
s := 1;
if k = 0 then s := 1
else for i := 1 to n - k do s := s*(k + i) div i
end;
{----------------------------------------------------------------------------------------}
begin
combination(90, 5, n1);
combination(89, 4, m);
p:=m/n1;
writeln('Вероятность появления шара с номером 90 равна ', p:6:4)
end.
Пример 2. Из пруда, в котором плавают 40 щук, выловили 5 щук, пометили их и пустили обратно в пруд. Во второй раз выловили 9 щук. Какова вероятность, что среди них окажутся ровно две помеченные щуки?
Математическое решение
Выясним общее число возможных событий, т.е. сколькими способами можно выловить 9 щук из 40 плавающих. Оно равно числу сочетаний из 40 по 9:

Сколько событий будут благоприятствовать тому, что среди этих 9 щук будут 2 помеченные.
Во-первых, две помеченные щуки можно выбрать из 5 ранее помеченных следующим количеством способов:

Во-вторых, к этим двум щукам надо добавить еще не помеченных 7 щук, которые можно выбрать из 35 не помеченных (ведь пять щук помеченные) количеством способов:

Значит, общее число благоприятствующих событий будет равно произведению числа способов из 5 по 2 на число способов из 35 по 7:

Тогда, искомая вероятность равна:

Вообще, если Y является m-подмножеством в n-множестве X и из X выбираются k-подмножество A, то вероятность того, что среди выбранных элементов содержится ровно r элементов из Y, равна:

Алгоритм
составления программы достаточно прост и поэтому сразу составим программу. Она будет такой:
Программа
Program Problem2;
uses WinCrt;
var
s1, s2, s3, p : real;
{----------------------------------------------------------------------------------------}
Procedure combination(n, k : integer; var s : real);
var
i : longint;
begin
s := 1;
if k = 0 then s := 1 else for
i := 1 to n - k do s := s*(k + i)/i
end;
{----------------------------------------------------------------------------------------}
begin
combination(40, 9, s1);
combination(35, 7, s2);
combination(5, 2, s3);
p := (s2*s3)/s1;
writeln('Вероятность появления двух помеченных щук равна ', p:6:4)
end.
Команда присваивания



Так на языке Паскаль обозначается команда присваивания. В чем ее сущность?

Команда присваивания "стирает" предыдущее значение переменной и "придает" ей новое значение. На языке Паскаль команда присваивания обозначается: := двоеточие и знак равно.
В нашей программе, переменной b присваивается значение a + 17, что равно 33, переменной c присваивается значение частного от деления переменной b на 3,

Чтобы понять значение терминов "стирает" и "придает" в определении команды присваивания, надо немного глубже рассмотреть "компьютерную физиологию", т.е., что происходит в компьютере при выполнении команды присваивания.
Для каждой переменной в оперативной памяти компьютера отводится место - ячейка памяти, куда компьютер заносит значение этой переменной. Каждая ячейка имеет свое имя по имени переменной в программе. В нашей программе под переменные отведено 3 ячейки с именами a, b, c.
При выполнении команды присваивания в ячейки с этими именами будут занесены соответствующие числа. Если в них была записана какая-то информация, то она уничтожится. Происходит процесс похожий на запись на магнитофонную ленту. При записи новой информации прежняя стирается.
В программе очень удобно помещать
В программе очень удобно помещать комментарии, чтобы при последующем прочтении она была понятна другим пользователям и программистам.
Комментарии - это тексты, объясняющие программу, но не влияющие на ее исполнение. Это различные объяснения, заголовки отдельных частей программы и т.д. Компьютер печатает комментарии вместе с текстом программы, но, выполняя программу, игнорирует их. Программа выполняется так, словно комментариев нет.
В нашей программе комментариев нет и это делает ее непонятной для других. Паскаль предусматривает располагать комментарии между фигурными скобками { ... } или между круглыми скобками со звездочками (* ... *). Всё, что находится в скобках, при выполнении программы игнорируется, но сохраняется в программе.
Почему допускается два способа записи комментариев?
Представьте себе ситуацию, когда внутри одного комментария надо разместить еще комментарий. Если внутри фигурных скобок будут размещены такие же скобки


Зато совершенно свободно вы можете сделать запись комментария в комментарии с помощью разных обозначений, например:
{ ... (* ... *) ... } или так (* ... { ... } ... *).
Правил для написания комментариев не существует. Однако, можно дать некоторые
рекомендации
по использованию комментариев в различных частях программы.
Вот несколько характерных случаев, когда комментарии желательны.
1. В начале программы сразу после заголовка целесообразно указать назначение программы, автора, дату написания и другие данные о программе, например:
Program
bid;
{Программа определения большего из двух чисел}
{автор программы Иванов Александр Петрович}
{программа составлена 12.10.1993}
{программа доработана 20.10.1993}
{программа протестирована 20.10.1993}
2. В описаниях переменных указывается назначение переменных:
var
a,{первое число}
b,{второе число}
c,{их наибольший общий делитель} ...
3. Объясняются действия, смысл и назначение которых непонятны:
c := a mod
b {остаток от деления a на b}
d := b*b - 4*a*c {вычисление дискриминанта квад. ур-я}
В программе желательны короткие и ясные комментарии. В противном случае текст программы может затеряться среди комментариев и программа станет еще менее ясной.
Составим программу для первого примера на основе второго способа.
Он основан на применении двух операций с целыми числами - деления (div) и нахождения остатка от деления (mod).
Посмотрите на примере, в чём состоит математика этого способа.
Находим цифру единиц: 342 mod 10 = 2.
Делим заданное число на 10, при этом уже найденная цифра единиц "отбрасывается": 342 div 10 = 34.
Находим цифру десятков: 34 mod 10 = 4.
Делим, оставшееся число 34 на 10, при этом цифра десятков "отбрасывается", а результатом будет цифра сотен:
34 div 10 = 3.
Дальнейшие операции такие же, как и в первом способе.
Программа
Program Problem;
uses WinCrt;
var
a, c, s, d, e, b, r : integer;
begin
write('Введите трехзначное число '); readln(a);
c := a; {Запоминается первоначальное число}
e := a mod 10; (* Цифра единиц *)
a := a div 10;
d := a mod 10; (* Цифра десятков *)
s := a div 10; (* Цифра сотен *)
b := e*100 + d*10 + s;
(* Число, записан. в обратном пор. *)
r := c - b; (* Разность чисел *)
writeln('Искомая разность равна ', r)
end.
ВЫВОДЫ
В программе можно использовать комментарии, которые записываются в фигурных скобках { ... } или в круглых скобках со звездочкой (* ... *). Повторная запись одних и тех же скобок недопустима. При записи комментария в комментарии надо использовать разные скобки.
Операция a mod
b выдает остаток от деления a на b. Если деление происходит нацело, то результат операции равен нулю.
Литература
1. Абрамов С.А., Зима Е.В. Начала информатики. - М.: Наука. Гл. ред. физ.-мат. лит., 1989.
2. Брудно А.Л., Каплвн Л.И. Московские олимпиады по программированию/Под ред. акад. Б.Н. Наумова. - 2-е изд., доп. и перераб. - М.: Наука. Гл. ред. физ.-мат. лит., 1990.
3. Васильев Н. Б., Гутенмахер В.Л., Раббот Ж.М., Тоом А.Л. Заочные математические олимпиады. - 2-е изд., перераб. - М.: Наука. Гл. ред. физ.-мат. лит., 1997.
4. Васюкова Н.Д., Тюляева В.В. Практикум по основам программирования. Язык ПАСКАЛЬ: Учеб. пособие для учащихся сред. спец. учеб. заведений. - М.: Высш. шк., 1991.
5. Дагене В.А. и др. 100 задач по программированию: Кн. для учащихся: Пер. с лит./В.А. Дагене, Г.К. Григас, К.Ф. Аугутис. - М.: Просвещение, 1993.
6. Джонс Ж., Харроу К. Решение задач в системе Турбо Паскаль/Пер. с англ.; Предисл. Ю.П. Широкого. - М.: Финансы и статистика, 1991.
7. Епанешников А., Епанешников В. Программирование в среде Turbo Pascal 7.0. - м.: "ДИАЛОГ-МИФИ", 1993.
8. Есаян В.И. Ефимов, Л.П. Лапицкая и др Информатика. Учеб. пособие. для пед. спец. высш. учеб. заведений/А. Р.. - М.: Просвещение, 1991.
9. Журналы "Информатика и образования", 1986-1994 гг. 17. Журналы "Квант", 1986-1994 гг.
10. Заварыкин В. М. и др. Численные методы: Учеб. пособие для студентов физ.-мат.
спец. пед. ин-тов/В.М. Заворыкин, В.Г. Житомирский, М.П. Лапчик. - М.: Просвещение, 1990.
11. Зубов В. С. Программирование на языке Turbo Pascal. "Фтлинъ". Москва. 1997г.
12. Офицеров Д.В., Старых В.А. Программирование в интегрированной среде Турбо-Паскаль: Справ. пособие. - Мн.: Беларусь, 1992.
13. Очков В. Ф., Пухначев Ю.В. 128 советов начинающему программисту. - М.: Энергоатомиздат, 1991.
14. Перминов О. Н. Программирование на языке Паскаль. "Радио и связь". Москва, 1988 г.
15. Скопец и др. Дополнительные главы по курсу математики. Учеб. пособие по факультативному курсу для учащихся 10 кл. Сборник статей. Сост. З.А.. Изд. 2-е, перераб. М., "Просвещение", 1974.
16. Тарасов Л.В. Мир, построенный на вероятности: Кн. для учащихся. - М.: Просвещение, 1984.
17. Тумасонис В., Дагене В., Григас Г. Паскаль. Руководства для программиста: Справочник: Пер. с литовск. - М.: Радио и связь, 1992.
18. Фаронов В. В. Турбо Паскаль (в 3-х книга). Книга 1. Основы Турбо Паскаля. - М.: Учебно-инженерный центр "МВТУ-ФЕСТО ДИДАКТИК", 1992.
19. Федоров А., Рогатин Д. Borland Pascal в среде Windows. "Диалектика", Киев, 1993 г.
Логические операции
| Логическая операция | Ее значение | Примеры
записи | Значение примера | ||||
| AND | Логическое "И" | (x<7) and
(x>3) | x меньше 7 и x больше 3 (3<x<7) | ||||
| OR | Логическое "ИЛИ" | (y>100) or (y<10) | y больше 100 или
y меньше 10 (y<10, y>100) | ||||
| NOT | Логическое "НЕ" | not (x=2) | не x равно 2 |

| a | b | a and
b | a or
b | ||||
| истина | истина | истина | истина | ||||
| истина | ложь | ложь | истина | ||||
| ложь | истина | ложь | истина | ||||
| ложь | ложь | ложь | ложь |
Остановимся немного подробнее на операции целочисленного деления (div) и операции, выдающей остаток от деления (mod).
Так, результатом целочисленного деления 17 на 5 будет 3:
17 div 5 = 3, а результатом деления меньшего числа на большее, будет 0:
46 div
200 = 0.
Делаем вывод, что при целочисленном деление дробная часть отбрасывается, сам термин "целочисленное деление" или "деление нацело" говорит сам за себя.
Операция a div b осуществляет целочисленное деление целого a на целое b.
Дробная часть при этом отбрасывается.
Еще одна интересная операция - остаток от деления a на b.
Понятно, что остатком от деления 17 на 5 будет число 2:
17 mod 5 = 2,
а вот чему будет равен остаток от деления меньшего числа на большее, например, 46 mod 200?
Оказывается, в этом случае, результатом операции будет число 46. Вот другие примеры:
34 mod
125 = 34,
120 mod 6 = 0.
Интересно, что остаток от деления любого целого числа на 10 будет равен последней цифре этого числа:
543 mod 10 = 3, 45 mod 10 = 5, 7 mod 10 = 7.
Рассмотрим задачу, которая показывает использование операций целочисленного деления и остатка от деления.
Пример 1. Найти разность между трехзначным числом и числом, составленным из тех же цифр, но взятых в обратном порядке.
При решении этой задачи, надо помнить, что компьютер не знает десятичной и позиционной формы записи чисел, так для него совершенно неизвестно, сколько в числе 342 сотен, десятков и единиц.
Это известно нам, потому что с раннего возраста мы используем такую форму записи чисел. Мы условились считать, что на первом месте слева стоит цифра единиц, на втором - цифра десятков, на третьем - цифра сотен и т.д.
Компьютеру это неизвестно! Он любое число переводит на язык двух цифр -

А для решения этой задачи нам необходимо знать цифры единиц, десятков и сотен заданного числа, чтобы затем переставить их, отсюда возникает первая задача - научить компьютер находить цифры числа, принадлежащие различным разрядам. Для этого можно использовать два способа.
Способ первый достаточно простой. Сущность которого в следующем.
Для определения цифры сотен делим данное число на 100 и остаток отбрасываем, т. е. выполняем целочисленное деление.
Для определения цифры десятков надо из данного числа вычесть сотни, результат разделить на 10 и остаток отбросить.
Для определения цифры единиц надо из данного числа вычесть сотни и десятки. Для записи числа теми же цифрами в обратном порядке, умножим цифру единиц на 100, сложим с цифрой десятков, умноженной на 10 и с цифрой сотен.
Далее из заданного числа вычитаем полученное новое. Например, для числа 342. Выполним целочисленное деление числа на 100, получим цифру сотен:
342 div 100 = 3;
вычитаем из 342 сотни 3*100 и результат делим на 10 - получим цифру десятков:
(342 - 3*100) div
10 = 4;
наконец, вычитаем из заданного числа сотни и десятки, получаем цифру единиц:
342 - 3*100 - 4*10 = 2.
Для записи числа в обратном порядке, умножаем цифру единиц 2 на 100 и складываем с цифрой десятков, умноженных на 10 (4*10) и прибавляем цифру сотен 3. Получим новое число, записанное теми же цифрами, но в обратном порядке:
2


Вычитаем: 342 - 243 = 99.
Программа
Program Problem1;
uses WinCrt;
var
a, s, d, e, b, r : integer;
begin
write('Введите трехзначное число '); readln(a);
s := a div 100;
d := (a - s*100) div 10;
e := a - s*100 - d*10;
b := e*100 + d*10 + s;
r := a - b;
writeln('Искомая разность равна ', r)
end.
Программа достаточно проста и понятна.
В разделе описаний переменным a, s, d, e, b, r устанавливается целый тип - integer.
Вводится трехзначное число и присваивается переменной a.
Переменной s присваивается результат целочисленного деления введенного числа a на 100. Это значение есть цифра сотен. Переменная d получает значение цифры десятков:
d := (a - s*100) div
10,
переменная e - это цифра единиц:
e := a - s*100 - d*10.
Дальнейшая работа программы понятна.
Математическое ожидание
Рассмотрим дискретную случайную величину X, которая принимает следующие значения x1, x2, ..., xk с вероятностями p1, p2, ..., pk. Произведем n независимых испытаний для определения значений величины X, и пусть каждое значение xi встретится ni раз (i = 1, 2, ..., k), так что n1 + n2 + ... + nk = n.
Этот процесс очень похож на n - кратное бросание игральной кости, а значения x1, x2, ..., xk на выпадение соответствующего числа очков (1, 2, 3, 4, 5, 6); n1, n2, n3, ..., nk
- на число выпадения этого числа очков.
Среднее арифметическое из полученных значений определяется формулой:

(каждое значение надо учитывать слагаемым столько раз, сколько раз оно встретилось!).
Представим среднее арифметическое


При большом числе испытаний (n) относительные частоты ni/n будут близки соответствующим вероятностям
ni/n = pi
= P(X = xi),
тогда, значение среднего арифметического x будет приблизительно равно

Определение. Математическим ожиданием MX дискретной случайной величины X называется сумма произведений всех ее возможных значений xi на их вероятности pi:

Если множество возможных значений дискретной случайной величины X бесконечно, то математическое ожидание будет выражаться суммой бесконечного ряда:

При этом мы всегда будем предполагать, что этот бесконечный ряд абсолютно сходится (т.е. имеет конечную сумму), в противном случае считается, что математическое ожидание случайной величины не существует.
Математическое ожидание MX называют также средним значением случайной величины X, подчеркивая тем самым статистический смысл этого понятия (статистическим аналогом математического ожидания служит среднее арифметическое из эмпирических значений случайной величины).
Надо заметить, что в отличие от среднего арифметического значения, которое само по себе является случайной величиной, так как зависит от числа испытаний, математическое ожидание является числом, которое связано только с законом распределения случайной величины.
Математическое ожидание MX называют еще центром распределения случайной величины X.
Это название произошло из-за аналогии с понятием центра тяжести для системы материальных точек, расположенных на одной прямой; если на оси x в k точках с координатами x1, x2, ..., xk сосредоточены массы p1, p2, ..., pk, то координата xc центра тяжести системы находится по формуле

для распределения вероятностей

и результат становится равным

Математическое ожидание и дисперсия непрерывной случайной величины
Определение. Математическим ожиданием M(X) непрерывной случайной величины X, плотностью вероятности которой является функция p(x), называется величина интеграла

если он сходится абсолютно, а дисперсией называется величина интеграла

если он сходится [где a = M(X)].
Легко заметить полную аналогию определений математического ожидания непрерывной и прерывной случайных величин. В формуле (5) суммирование заменено интегрированием (что вполне естественно для непрерывной случайной величины). Роль xi играет непрерывно изменяющаяся переменная x. Так как p(x)



Пример 1. Минутная стрелка электрических часов передвигается скачками поминутно. Вы бросили взгляд на часы. Они показывают a минут. Тогда для Вас истинное время в данный момент будет случайная величина. Найти ее функцию распределения.
Решение
Функция распределения истинного времени равна 0 для всех x





Она непрерывна всюду, а производная ее непрерывна во всех точках за исключением двух: x = a и x = a + 1.
Программа
Program
Function_Continuous1;
uses WinCrt;
var
a : integer;
x, alfa : real;
{---------------------------------------------------------------------------------------}
Function Fx(a : integer; x, alfa : real) : real;
begin
if x < a
then Fx := 0
else if x = a + alfa
then Fx := alfa
else Fx := 1
end;
{---------------------------------------------------------------------------------------}
begin
write('Введите число минут, которое показывает минутная стрелка ');
readln(a);
write('Введите значение аргумента функции распределения '); readln(x);
if (x - a < 1) and (x - a > 0) then alfa := x - a
else alfa := 0;
write('Значение функции распределения равно ', Fx(a, x, alfa):4:6)
end.
Пример 2. Случайная величина X равномерно распределена. Ее плотность вероятности p(x) = A, если a


Решение
По формуле (3') получаем:



Программа
Program Problem2;
uses WinCrt;
var
AA, a, b : real;
begin
write('Введите левую границу интервала '); readln(a);
write('Введите правую границу интервала '); readln(b);
AA := 1/(b - a);
writeln('Значение коэффициента A равно ', AA:6:6)
end.
Метод статистических испытаний
Статистические испытания предполагают многократное повторение однотипных испытаний. Результат любого отдельного испытания случаен и сам по себе какого-либо интереса не представляет. В то же время совокупность большого числа подобных результатов оказывается весьма полезной. Она обнаруживает определенную устойчивость (ее называют статистической устойчивостью), которая позволяет количественно описать явление, исследуемое в данных испытаниях. Рассмотрим специальный метод исследования случайных процессов, основанный на статистических испытаниях. Его так и называют - метод статистических испытаний. Другое название этого метода, которое используется чаще, - метод Монте-Карло.
Прежде, чем рассмотреть непосредственное применение этого метода надо познакомится с понятием геометрической вероятности.
Наиболее вероятное число событий биномиального распределения
Из распределения вероятностей по биномиальному закону видно, что вероятность вначале возрастает, а затем убывает. Естественно возникает вопрос о числе событий, имеющей наибольшую вероятность.

При возрастании m от 0 до n-1 это отношение убывает от np/q до p/nq. Если np > q и nq > p, то рассматриваемое отношение переходит от значений больших 1, к значениям, меньшим 1. А это означает, что вероятность P(X = m) сначала возрастает, а затем убывает. И лишь в крайних случаях, когда np < q или nq < p, вероятности P(X = m) изменяются монотонно.
Во всех случаях наиболее вероятное значение X = m0 находится из неравенств

откуда следует, что

Этому неравенству удовлетворяет только одно целое число m0 , если только np + p не является целым числом: в последнем случае имеются два наиболее вероятных значения X = np + p - 1 и X = np + p. В частном случае, когда произведение np - целое число, оно и является наиболее вероятным значением величины X.
Пример 5. Вероятность появления бракованной детали равна 0.02. Определить наиболее вероятное число годных деталей в партии из 1000 штук, а также математическое ожидание и дисперсию случайной величины.
{ Биномиальный закон распределения вероятностей }
{ Наиболее вероятное число исходов }
Program Problem5;
uses WinCrt;
var
p, m1, m2, mx, dx : real;
n, m0 : integer;
{----------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите общее число деталей в партии '); readln(n);
write('Введите вероятность появления бракованной детали ');
readln(p);
m1 := n*p + p - 1; m2 := n*p + p;
if (m1 = m2) and (m1 = trunc(m1)) then m0 := trunc(m1)
else m0 := trunc(m2);
mx := n*p; dx := n*p*(1 - p);
write('Наиболее вероятное число бракованных деталей ');
writeln(' в этой партии равно ', m0);
writeln('Математическое ожидание равно ', mx:1:6);
writeln('Дисперсия случайной величины равна ', dx:1:6)
end.
Из этого примера видно, что наиболее вероятное число появление событий при малой вероятности и большом числе исходов - m0, равно математическому ожиданию дискретной случайной величины mx (m0 = mx).
Некоторые замечательные функции
6.1. Функция Бесселя
Для



Легко видеть, что

Для определения слагаемых применим рекуррентную формулу

В качестве начальных значений суммы и слагаемого использовать член ряда при k = 0, равный

Для вычисления значения функции при k = 0, необходимо использовать функции вычисления степени c основанием

Функция вычисления степени.
Function
Extent(x : real; n : integer) : real;
var
i : integer;
E : real;
begin
E := 1;
if n = 0 then E := 1
else for
i := 1 to n do E := E*x/2;
Extent := E
end;
Функция вычисления факториала.
Function Fakt(n : integer) : longint;
var
i : integer;
F : longint;
begin
F := 1;
if n = 0 then F := 1
else for
i := 1 to n do F := F*i;
Fakt := F
end;
А теперь составим функцию вычисления всей суммы

Function J(x, eps : real; n : integer) : real;
var
y, jj : real;
k : integer;
begin
k := 0; y := Extent(x, n)/Fakt(n); jj := 0;
repeat
jj := jj + y;
k := k + 1;
y := -y*x*x/(4*k*(n + k))
until abs(y) < eps;
J := jj
end;
Программа
Program Bessel;
uses WinCrt;
var
n : integer;
x, eps : real;
{----------------------------------------------------------------------------------------}
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Function Extent(x : real; n : integer) : real;
var
i : integer;
E : real;
begin
E := 1;
if n = 0 then E := 1
else for
i := 1 to n do E := E*x/2;
Extent := E
end;
{----------------------------------------------------------------------------------------}
Function Fakt(n : integer) : longint;
var
i : integer;
F : longint;
begin
F := 1;
if n = 0 then F := 1
else for
i := 1 to n do F := F*i;
Fakt := F
end;
{----------------------------------------------------------------------------------------}
Function J(x, eps : real; n : integer) : real;
var
y, jj : real;
k : integer;
begin
k := 0; y := Extent(x, n)/Fakt(n); jj := 0;
repeat
jj := jj + y;
k := k + 1;
y := -y*x*x/(4*k*(n + k))
until abs(y) < eps;
J := jj
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите значение x '); readln(x);
write('Введите значение n '); readln(n);
write('Введите точность вычисления '); readln(eps);
writeln('Значение функции Бесселя равно ', J(x, eps, n):6:t(eps))
end.
6.2. Гамма-функция Эйлера
Рассмотрим (вместе с Эйлером) бесконечное произведение

считая x отличным от нуля и от всех целых отрицательных чисел.
Легко представить его общий множитель так:

отсюда вытекает, что наше произведение (абсолютно) сходится.
Определяемая им функция

Используя формулу





Теперь надо оставить функцию для вычисления степени действительного положительного аргумента a с любым действительным показателем x. Для этого достаточно воспользоваться соотношением:

Function
Extent_real(a, x : real) : real;
begin
Extent_real := exp(x*ln(a))
end;
Теперь можно составить основную функцию для вычисления гамма-функции.
Function G(x, eps : real) : real;
var
n : longint;
g1, gg : real;
begin
n := 1; gg := Extent_real((n + 1)/n, x)/(x*(x + n));
repeat
n := n + 1;
gg := gg*n*Extent_real((n + 1)/n, x)/(x + n);
n := n + 1;
g1 := gg*n*Extent_real((n + 1)/n, x)/(x + n)
until abs(g1 - gg) < eps;
G := gg
end;
Программа
Program
Gamma_function;
uses WinCrt;
var
x, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - количества знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Function Extent_real(a, x : real) : real;
begin
Extent_real := exp(x*ln(a))
end;
{----------------------------------------------------------------------------------------}
Function G(x, eps : real) : real;
var
n : longint;
g1, gg : real;
begin
n := 1; gg := Extent_real((n + 1)/n, x)/(x*(x + n));
repeat
n := n + 1;
gg := gg*n*Extent_real((n + 1)/n, x)/(x + n);
n := n + 1;
g1 := gg*n*Extent_real((n + 1)/n, x)/(x + n)
until abs(g1 - gg) < eps;
G := gg
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите значение аргумента '); readln(x);
write('Введите точность вычисления '); readln(eps);
writeln('Значение гамма-функции равно ', G(x, eps):6:t(eps))
end.
Так как n- е частичное произведение имеет вид


Написав аналогичную формулу для


и мы приходим к простому и важному соотношению:

Если вы выполняли предыдущую программу для различных значений аргумента, то смогли убедиться, что точность вычисления невелика, даже при достаточно большом значении n.
Формула

Для этого составим следующую функцию:
Function
Gamma(x, eps : real) : real;
begin
x := x - 1;
Gamma := x*G(x, eps)
end;
Program
Gamma_function;
uses WinCrt;
var
x, eps, gg : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - количества знаков после запятой }
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Function Extent_real(a, x : real) : real;
begin
Extent_real := exp(x*ln(a))
end;
{----------------------------------------------------------------------------------------}
Function G(x, eps : real) : real;
var
n : longint;
g1, gg : real;
begin
n := 1; gg := Extent_real((n + 1)/n, x)/(x*(x + n));
repeat
n := n + 1;
gg := gg*n*Extent_real((n + 1)/n, x)/(x + n);
n := n + 1;
g1 := gg*n*Extent_real((n + 1)/n, x)/(x + n)
until abs(g1 - gg) < eps;
G := gg
end;
{----------------------------------------------------------------------------------------}
Function Gamma(x, eps : real) : real;
begin
x := x - 1;
Gamma := x*G(x, eps)
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите значение аргумента '); readln(x);
write('Введите точность вычисления '); readln(eps);
if (x < 2) and (x > 1) then gg := Gamma(x, eps)
else gg := G(x, eps);
writeln('Значение гамма-функции равно ', gg:6:t(eps))
end.
Если положить x равным натуральному числу m, то получим рекуррентную формулу

Так как


Эта формула дает еще одну возможность уточнить значения функции для натуральных значений аргумента. Для вычисления по этой формуле составим еще одну функцию.
Function G_natural(m : integer) : longint;
var
i : integer;
g : longint;
begin
g := 1;
for i := 2 to m do
g := g*i;
G_natural := g
end;
Программа
изменится и станет такой:
Program
Gamma_function;
uses WinCrt;
var
x, eps, gg : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - количества знаков после запятой }
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
Function Extent_real(a, x : real) : real;
begin
Extent_real := exp(x*ln(a))
end;
{----------------------------------------------------------------------------------------}
Function G(x, eps : real) : real;
var
n : longint;
g1, gg : real;
begin
n := 1; gg := Extent_real((n + 1)/n, x)/(x*(x + n));
repeat
n := n + 1;
gg := gg*n*Extent_real((n + 1)/n, x)/(x + n);
n := n + 1;
g1 := gg*n*Extent_real((n + 1)/n, x)/(x + n)
until abs(g1 - gg) < eps;
G := gg
end;
{----------------------------------------------------------------------------------------}
Function Gamma(x, eps : real) : real;
begin
x := x - 1;
Gamma := x*G(x, eps)
end;
{----------------------------------------------------------------------------------------}
Function G_natural(m : integer) : longint;
var
i : integer;
g : longint;
begin
g := 1;
for i := 2 to m do
g := g*i;
G_natural := g
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите значение аргумента '); readln(x);
write('Введите точность вычисления '); readln(eps);
if x = trunc(x)
then gg := G_natural(trunc(x))
else
if (x < 2) and (x > 1)
then gg := Gamma(x, eps)
else gg := G(x, eps);
writeln('Значение гамма-функции равно ', gg:6:t(eps));
end.
Еще одну важную формулу для функции



Мы находим:


Это - формула Вейерштрасса.
Библиотека часто встречающихся процедур и функций
55. Вычисление числа e.
Procedure number_e(eps : real; var
e : real);
var
n : integer;
u : real;
begin
e := 0; u := 1; n := 1;
repeat
e := e + u;
u := u/n; n := n + 1
until 3*u <= eps;
end;
56. Вычисление корней любой степени из произвольного числа.
Procedure Radical(n : integer ; x, eps : real; var b : real);
var
n : integer;
z, m, u : real;
begin
b := 1; u := 1; n := 1;
repeat
u := (m - n + 1)*x*u/n; b := b + u; n := n+1
until abs(u) <= eps;
end;
57. Процедура вычисления бесконечного произведения

Procedure
Multiplication(eps : real; var Mult : real);
var
n : longint;
Mult1 : real;
begin
n := 2; Mult1 := 1;
repeat
Mult1 := Mult1*(1 - 1/sqr(n));
n := n + 1;
Mult := Mult1*(1 - 1/sqr(n))
until abs(Mult - Mult1) < eps
end;
58. Процедура вычисления числа

Procedure Wallis(eps : real; var Mult : real);
var
n : longint;
Mult1 : real;
begin
n := 1; Mult := 1;
repeat
Mult := Mult*(4*sqr(n)/(4*sqr(n)-1));
n := n + 1;
Mult1 := 4*sqr(n)/(4*sqr(n)-1)
until Mult1 < eps
end;
59. Процедур вычисления эллиптического интеграла 1-го рода через бесконечное произведение.
Procedure Elliptic(k, eps : real; var Kk : real);
var
Kk1 : real;
begin
Kk1 := k;
repeat
k := (1 - sqrt(1 - sqr(k)))/(1 + sqrt(1 - sqr(k)));
Kk1 := Kk1*(1 + k);
k := (1 - sqrt(1 - sqr(k)))/(1 + sqrt(1 - sqr(k)));
Kk := Kk1*(1 + k);
until abs(Kk1 - Kk) < eps;
Kk := Kk*Pi/2
end;
60. Рекуррентная функция вычисления интеграла вероятностей.
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
61. Процедура вычисления интеграла

Procedure
Integral(x, eps : real; var I : real);
var
n : integer;
u : real;
begin
u := x; n := 1; I := 0;
repeat
I := I + u;
n := n + 1;
u := -(u*x*x*(2*n - 3))/((2*n - 2)*sqr(2*n - 1))
until abs(u) < eps
end;
62. Процедура вычисления эллиптического интеграла 2-го рода с помощью интегрирования рядов.
Procedure Elliptic2(k, eps : real; var Ek : real);
var
n : integer;
u : real;
begin
u := k*k/4; n := 1; Ek := 0;
repeat
Ek := Ek + u;
n := n + 1;
u := (u*k*k*(2*n - 1)*(2*n - 3))/(4*n*n);
until abs(u) < eps;
Ek := Pi*(1 - Ek)/2
end;
63. Функция Бесселя:

Function
J(x, eps : real; n : integer) : real;
var
y, jj : real;
k : integer;
begin
k := 0; y := Extent(x, n)/Fakt(n); jj := 0;
repeat
jj := jj + y;
k := k + 1;
y := -y*x*x/(4*k*(n + k))
until abs(y) < eps;
J := jj
end;
64. Функция вычисления степени положительного действительного числа с произвольным действительным показателем.
Function
Extent_real(a, x : real) : real;
begin
Extent_real := exp(x*ln(a))
end;
65. Функции для вычисления гамма-функции.
Для произвольного действительного аргумента x, отличного от нуля и от всех целых отрицательных чисел.
Function G(x, eps : real) : real;
var
n : longint;
g1, gg : real;
begin
n := 1; gg := Extent_real((n + 1)/n, x)/(x*(x + n));
repeat
n := n + 1;
gg := gg*n*Extent_real((n + 1)/n, x)/(x + n);
n := n + 1;
g1 := gg*n*Extent_real((n + 1)/n, x)/(x + n)
until abs(g1 - gg) < eps;
G := gg
end;
Вычисление гамма-функции для значений аргумента из промежутка (1, 2)
Function Gamma(x, eps : real) : real;
begin
x := x - 1;
Gamma := x*G(x, eps)
end;
Вычисление гамма-функции натурального аргумента.
Function
G_natural(m : integer) : longint;
var
i : integer;
g : longint;
begin
g := 1;
for i := 2 to m do
g := g*i;
G_natural := g
end;
Упражнения
194. Вычислить сумму членов рядов, заданных формулами общего члена. Число членов ряда задается пользователем.

195. Составьте функции для нахождения с указанной точностью числа

a)

б) ряд Леонардо Эйлера:

196. Составьте функции для вычисления с указанной точностью значений тригонометрических функций путем вычисления следующих рядов:
а)

Для вычисления значения члена ряда использовать рекуррентную формулу

б)

Для определения значения члена ряда использовать формулу

197. Дано действительное x. Вычислить приближенное значение бесконечной суммы:

Нужное приближение считается полученным, если вычислена сумма нескольких первых слагаемых, и очередное слагаемое оказалось по модулю меньше 0.00001.
198. Вычислить приближенное значение бесконечной суммы (справа от каждой суммы дается ее точное значение, с которым можно сравнить полученный результат):
а)

б)

в)


г)


Нужное приближение считается полученным, если вычислена сумма нескольких первых слагаемых, и очередное слагаемое оказалось по модулю меньше данного положительного числа eps.
199. Дано: натуральное n, действительное x. Вычислить:
а)


в)

200. Дано: действительные a, h, натуральное n. Вычислить


201. Дано: натуральное n, действительное x. Вычислить:

202. Вычислить:
а)


в)


203. Вычислить сумму членов ряда

с точностью до члена ряда меньшего 0.0000001.
204. Установить, сходятся ли следующие ряды:
а)



205. Составить программу вычисления бесконечного произведения:

Частичное произведение имеет вид

где C - эйлерова постоянная, а


206. Эйлером были найдены следующие разложения тригонометрических функций в бесконечные произведения:
1)

2)

Составьте программы вычисления этих произведений и вычислите значения sinx и cosx с заданной точностью.
207. Дано натуральное n. Получить:
а)


в)

г)

д)


208. Дано натуральное n. Получить


209. Вычислить интеграл

Ответы
К заданию 1
Program
Task1; {Вычисление sinx с помощью ряда}
uses WinCrt;
var
n, k : integer;
x, e, eps, sin, u : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
begin
write('Задайте точность вычисления '); readln(eps);
write('Введите значение аргумента в радианах '); readln(x);
u := x; n := 2;
sin := x;
repeat
u := -u*x*x/((2*n-1)*(2*n-2));
sin := sin + u;
n := n + 1
until abs(u) < eps;
write('Значение sin( ', x:1:t(eps), ' ) равно ', sin:3:t(eps));
writeln(' с точностью до ', eps:1:t(eps))
end.
К
заданию 2
Program Task2;
uses WinCrt;
var
n : integer;
p, u, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function
t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
begin
write(' Укажите точность вычисления числа пи '); readln(eps);
u := 1; p := 0; n := 1;
repeat
p := p + u;
n := n + 1;
u := -u*(2*n - 3)/(2*n - 1)
until abs(u) < eps;
write('Число Пи равно ', 4*p:1:t(eps), ' с точностью до ');
writeln(eps:1:t(eps))
end.
К
заданию 3
Program Task3;
uses WinCrt;
var
k : integer;
a, u, z, z1, e, eps : real;
{----------------------------------------------------------------------------------------}
{ Функция вычисления порядка - кол-во знаков после запятой }
Function t(eps : real) : integer;
var
k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
{----------------------------------------------------------------------------------------}
begin
write('Введите значение a>1 '); readln(a);
write('Задайте точность eps '); readln(eps);
u := 1; z := 0;
repeat
u := u*a;
z := z + 1/(1 + u);
z1 := z + 1/(1 + u*a)
until abs(z1 - z) < eps;
write('Сумма ряда равна ', z1:1:t(eps));
writeln(' с точностью до ', eps:1:t(eps))
end.
К
заданию 4
Program Task4;
uses WinCrt;
n : integer;
var
a : longint;
{----------------------------------------------------------------------------------------}
Function c(a : integer) : longint;
var
s, z : integer;
begin
z := 0;
repeat
s := a mod 10;
z := z + s;
a := a div 10
until s = 0;
c := z
end;
{----------------------------------------------------------------------------------------}
begin
a := 7;
n := 1;
while n <= 1000 do
begin
a := c(a*a);
n := n + 1
end;
writeln(n - 1, '- й член последовательности равен ', a)
end.