Чуть-чуть истории
Теория графов - довольно молодая наука (по сравнению, скажем, с геометрией). В 1736 году Санкт-Петербургская академия наук опубликовала труд Леонарда Эйлера, где рассматривалась задача о кенигсбергских1) мостах ("Можно ли, пройдя все городские мосты ровно по одному разу, вернуться в исходную точку?"). Это была первая работа по будущей теории графов.
Особенно приятно то, что в данном случае Россия - родина пусть и не новой породы слонов, но зато нового научного направления!
Деревья
Дерево - это частный случай графа, наиболее широко применяемый в программировании.
Дерево частотного словаря
Дерево частотного словаря - это результат построения дерева двоичного поиска не для чисел, а для слов некоторого текста. Генерирование дерева частотного словаря полезно при подсчете количества вхождений каждого слова в некоторый текст.
Приведем описание структуры этого дерева:
type ukazatel = ^tree; derevo = record slovo : string[20]; kolichestvo : integer; levyj : ukazatel; pravyj: ukazatel; end;
Дерево двоичного поиска
Дерево двоичного поиска для множества чисел S - это размеченное бинарное дерево, каждой вершине которого сопоставлено число из множества S, причем все пометки удовлетворяют следующим условиям:
существует ровно одна вершина, помеченная любым числом из множества S;все пометки левого поддерева строго меньше, чем пометка текущей вершины;все пометки правого поддерева строго больше, чем пометка текущей вершины.
Если выражаться простым языком, то структура дерева двоичного поиска подчиняется простому правилу: "если больше - направо, если меньше - налево".
Например, для набора чисел 7, 3, 5, 2, 8, 1, 6, 10, 9, 4, 11 получится такое дерево (см. рис. 11.14).
Для того чтобы правильно учесть повторения чисел, можно ввести дополнительное поле, которое будет хранить количество вхождений для каждого числа.
Более подробно процессы построения и анализа дерева бинарного поиска будут изложены в следующей лекции, посвященной алгоритмам, использующим деревья и графы.

Рис. 11.14. Дерево двоичного поиска
Графы: определения и примеры
Итак, перейдем к изложению некоторых понятий современной теории графов.
Иерархический список
Собственно, этот способ представления графов является всего лишь внутренней реализацией списка смежности: в одном линейном списке содержатся номера "начальных вершин", а в остальных - номера смежных вершин или указатели на эти вершины. В качестве примера (см. рис. 11.11) приведем иерархический список, задающий орграф, изображенный на рис. 11.6.
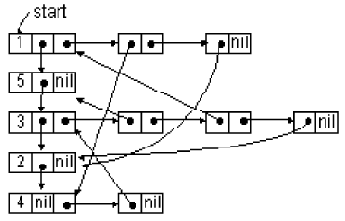
Рис. 11.11. Пример иерархического списка
type uk_versh = ^vershina; uk_duga = ^duga vershina = record number : integer; sled_vershina : uk_versh; spisok_dug : uk_duga end; duga = record konec_dugi : uk_versh; sled_duga : uk_duga; end;
Очевидное преимущество такого способа представления графов заключается в экономичном использовании памяти. И даже небольшая избыточность данных, к которой приходится прибегать в случае неориентированного графа, задавая каждое ребро как две дуги, искупается гибкостью всей структуры, что особенно удобно при необходимости частых перестроений в процессе работы программы.
Если в приведенные описания типов данных добавить поля, которые могли бы хранить веса вершин и дуг, то таким же способом можно задавать и взвешенные графы (орграфы).
Неориентированные графы
Граф - это двойка <V, E>, где V - непустое множество вершин, а Е - множество ребер, соединяющих эти вершины попарно2). Две вершины, связанные между собой ребром, равноправны, и именно поэтому такие графы называются неориентированными: нет никакой разницы между "началом" и "концом" ребра.
| Семья | Люди | Родственные связи |
| Город | Перекрестки | Улицы |
| Сеть | Компьютеры | Кабели |
| Домино | Костяшки | Возможность |
| Дом | Квартиры | Соседство |
| Лабиринт | Развилки и тупики | Переходы |
| Метро | Станции | Пересадки |
| Листок в клеточку | Клеточки | Наличие общей границы |
Говоря простым языком, граф - это множество точек (для удобства изображения - на плоскости) и попарно соединяющих их линий (не обязательно прямых). В графе важен только факт наличия связи между двумя вершинами. От способа изображения этой связи структура графа не зависит.
Например, три графа на рис. 11.1 совпадают, а два графа на рис. 11.2 - различны.

Рис. 11.1. Три способа изображения одного графа
Из приведенного выше определения вытекает, что в графах не бывает петель - ребер, соединяющих некоторую вершину саму с собой (см. рис. 11.3). Кроме того, в классическом графе не бывает двух различных ребер, соединяющих одну и ту же пару вершин.
Ребро е и вершина v называются инцидентными друг другу, если вершина v является одним из концов ребра е.

Рис. 11.2. Пример двух разных графов
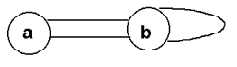
Рис. 11.3. Псевдограф
Любому ребру инцидентно ровно две вершины, а вот вершине может быть инцидентно произвольное количество ребер, это количество и определяет степень вершины. Изолированная вершина вообще не имеет инцидентных ей ребер (ее степень равна 0).
Две вершины называются смежными, если они являются разными концами одного ребра (иными словами, эти вершины инцидентны одному ребру). Аналогично, два ребра называются смежными, если они инцидентны одной вершине.
Путь в графе - это последовательность вершин (без повторений), в которой любые две соседние вершины смежны. Например, в графе, изображенном на рис. 11.1, есть два различных пути из вершины a в вершину с: adbc и abc.
Вершина v достижима из вершины u, если существует путь, начинающийся в u и заканчивающийся в v.
Граф называется связным, если все его вершины взаимно достижимы.
Компонента связности - это максимальный связный подграф. В общем случае граф может состоять из произвольного количества компонент связности. Заметим, что любая изолированная вершина является отдельной компонентой связности. На рис. 11.4 изображен граф, состоящий из четырех компонент связности: [abhk], [gd], [c] и [f].
Длина пути - количество ребер, из которых этот путь состоит. Например, длина уже упомянутых путей adbc и abc (см. рис. 11.1) - 3 и 2 соответственно.

Рис. 11.4. Несвязный граф
Говорят, что вершина v принадлежит k-му уровню относительно вершины u, если существует путь из u в v длиной ровно k ребер. Одна и та же вершина может относиться к разным уровням. Например, в графе, изображенном на рис. 11.1, относительно вершины a существует 4 уровня:
0) a;1) b, d;2) b, d, c (пути adb, abd, abc);3) c (путь adbc).
Расстояние между вершинами u и v - это длина кратчайшего пути от u до v. Из этого определения видно, что расстояние между вершинами a и c в графе на рис. 11.1 равно 2.
Цикл - это замкнутый путь. Все вершины в цикле, кроме первой и последней, должны быть различны. Например, циклом является путь abda в графе на рис. 11.1.
Эйлеров граф - это граф, в котором существует путь или цикл, содержащий все ребра графа (вершины могут повторяться). Именно такие графы положительно решают упомянутую в начале лекции задачу о кенигсбергских мостах. Например, граф на рис. 11.5 является Эйлеровым: искомым путем в нем будет dbacfbcd.
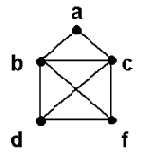
Рис. 11.5. Граф Эйлера
Гамильтонов граф - это граф, в котором существует путь или цикл (без повторений), содержащий все вершины графа (см. рис. 11.5; искомый цикл: abdfca).
Ориентированные графы
Орграф - это граф, все ребра которого имеют направление. Такие направленные ребра называются дугами. На рисунках дуги изображаются стрелочками (см. рис. 11.6).

Рис. 11.6. Орграф
В отличие от ребер, дуги соединяют две неравноправные вершины: одна из них называется началом дуги (дуга из нее исходит), вторая - концом дуги (дуга в нее входит). Можно сказать, что любое ребро - это пара дуг, направленных навстречу друг другу.
Если в графе присутствуют и ребра, и дуги, то его называют смешанным.
Все основные понятия, определенные для неориентированных графов (инцидентность, смежность, достижимость, длина пути и т.п.), остаются в силе и для орграфов - нужно лишь заменить слово "ребро" словом "дуга". А немногие исключения связаны с различиями между ребрами и дугами.
Степень вершины в орграфе - это не одно число, а пара чисел: первое характеризует количество исходящих из вершины дуг, а второе - количество входящих дуг.
Путь в орграфе - это последовательность вершин (без повторений), в которой любые две соседние вершины смежны, причем каждая вершина является одновременно концом одной дуги и началом следующей дуги. Например, в орграфе на рис. 11.6 нет пути, ведущего из вершины 2 в вершину 5. "Двигаться" по орграфу можно только в направлениях, заданных стрелками.
| Чайнворд | Слова | Совпадение последней и первой букв (возможность связать два слова в цепочку) |
| Стройка | Работы | Необходимое предшествование (например, стены нужно построить раньше, чем крышу, т. п.) |
| Обучение | Курсы | Необходимое предшествование (например, курс по языку Pascal полезно изучить прежде, чем курс по Delphi, и т.п.) |
| Одевание ребенка | Предметы гардероба | Необходимое предшествование (например, носки должны быть надеты раньше, чем ботинки, и т.п.) |
| Европейский город | Перекрестки | Узкие улицы с односторонним движением |
| Организация | Сотрудники | Иерархия (начальник - подчиненный) |
Основные определения
Существует довольно много равносильных определений деревьев, вот лишь некоторые из них.
Дерево - это связный граф без циклов. Дерево - это связный граф, в котором при N вершинах всегда ровно N-1 ребро.Дерево - это граф, между любыми двумя вершинами которого существует ровно один путь.
Аналогичным образом определяется и ориентированное дерево - как орграф, в котором между любыми двумя вершинами существует не более одного пути.
| Армия | Солдаты и офицеры | Иерархия (командир - подчиненный) |
| Династия (родословная по мужской4 линии) | Монархи | Отношение "отец - сын" |

Рис. 11.12. Корневое дерево высоты 3
Мы будем изучать и использовать только один частный случай ориентированных деревьев - корневые деревья (см. рис. 11.12).
Корневое дерево - это ориентированное дерево, в котором можно выделить вершины трех видов: корень, листья (другое их название: терминальные вершины) и остальные вершины (нетерминальные); причем должны выполняться два обязательных условия:
из листьев не выходит ни одна дуга; из других вершин может выходить сколько угодно дуг;в корень не заходит ни одна дуга; во все остальные вершины заходит ровно по одной дуге.
Традиционно в математике и в родственных ей науках (в том числе и в теоретическом программировании) деревья "растут" вниз головой: это делается просто для удобства наращивания листьев в случае необходимости. Таким образом, на рисунках корень дерева оказывается самой верхней вершиной, а листья - самыми нижними.
Предок вершины v - это вершина, из которой исходит дуга, заходящая в вершину v. Потомок вершины v - это вершина, в которую заходит дуга, исходящая из вершины v. В этих терминах можно дать другие определения понятиям корень и лист: у корня нет предков, у листа нет потомков.
Бинарное дерево - это корневое дерево, каждая вершина которого имеет не более двух потомков. В таком случае иногда говорят о левом потомке и правом потомке для текущей вершины.
Высота корневого дерева - это максимальное количество дуг, отделяющих листья от корня. Если дерево не взвешенное, то его высота - это просто расстояние от корня до самого удаленного листа.
И в заключение мы приведем определение, связывающее произвольные графы с деревьями более плотно.
Каркас графа - это дерево, полученное после выбрасывания из графа некоторых ребер (см. рис. 11.13).
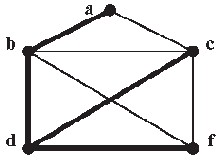
Рис. 11.13. Каркас графа
Примером каркаса является (корневое) дерево кратчайших путей от некоторой выделенной вершины (она будет корнем каркаса) до всех остальных вершин графа.
Представление бинарного дерева
Разновидностью описанного выше частного случая является бинарное корневое дерево: каждая его вершина имеет не более двух потомков:
type ukazatel = ^tree; tree = record znachenie : integer; left_sibling : ukazatel; right_sibling: ukazatel; end;
Представление корневого дерева
Этот способ подходит только для тех корневых деревьев, у которых точно известно максимальное количество потомков для любой вершины.
type ukazatel = ^tree; tree = record znachenie : integer; siblings : array[1..S] of ukazatel; end;
Разумеется, в общем случае значение переменной S (количество потомков) может достигать N-1 (N - количество всех вершин в дереве). Однако ясно, что в такой ситуации особого смысла в динамической древесной структуре нет: экономии памяти не получается. Гораздо лучше, если у всех вершин примерно одинаковое и заранее известное количество потомков.
Примеры использования деревьев
Здесь мы ограничимся только примерами использования бинарных корневых деревьев: именно такой вид графа чаще всего применяется в программировании.
Списки смежности
Этот способ задания графов подразумевает, что для каждой вершины будет указан список всех смежных с нею вершин (для орграфа - список вершин, являющихся концами исходящих дуг). Конкретный формат входного файла, содержащего списки смежности, необходимо обговорить отдельно. Например, в нашем случае начальная вершина отделена от списка смежности двоеточием:
<номер_начальной_вершины>: <номера_смежных_вершин>
Наиболее естественно применять этот способ для задания орграфов, однако и для остальных вариантов он тоже подходит.
В качестве примера приведем списки смежности, задающие все те же три графа, изображенные на рис. 11.5, рис. 11.6 и рис. 11.7 (см. рис. 11.10).
| a: b c b: c d f c: d f d: f | 1: 2 4 3: 1 2 5 4: 3 | b: a 1 c 2 d 10 c: a 10 d 3 |
Список ребер
Этот способ задания графов наиболее удобен для внешнего представления входных данных. Пусть каждая строка входного файла содержит информацию об одном ребре (дуге):
<номер_начальной_вершины> <номер_конечной_вершины> [<вес_ребра>]
В качестве примера приведем списки ребер (дуг), задающие те же три графа с рис. 11.5, рис. 11.6 и рис. 11.7 (см. рис. 11.9).
| a b a c b c b d c d c f f d b f | 1 2 1 4 3 1 3 2 3 5 4 3 | a b 1 a c 10 b c 2 b d 10 c d 3 |
Если задается ориентированный граф, то номера вершин понимаются как упорядоченная пара, а если граф неориентированный - как неупорядоченная.
Способы представления деревьев
Поскольку любое дерево является графом, то его можно задавать любым из способов, перечисленных в п. "Способы представления графов". Однако существуют и специальные способы представления, предназначенные только для деревьев. Мы рассмотрим только два наиболее распространенных частных случая.
Способы представления графов
Существует довольно большое число разнообразных способов представления графов. Однако мы изложим здесь только самые полезные с точки зрения программирования.
Взвешенные графы
Взвешенный (другое название: размеченный) граф (или орграф) - это граф (орграф), некоторым элементам которого (вершинам, ребрам или дугам) сопоставлены числа. Наиболее часто встречаются графы с помеченными ребрами. Числа-пометки носят различные названия: вес, длина, стоимость.
Замечание: Обычный (не взвешенный) граф можно интерпретировать как взвешенный, все ребра которого имеют одинаковый вес 1.
Длина пути во взвешенном (связном) графе - это сумма длин (весов) тех ребер, из которых состоит путь. Расстояние между вершинами - это, как и прежде, длина кратчайшего пути. Например, расстояние от вершины a до вершины d во взвешенном графе, изображенном на рис. 11.7, равно 6.

Рис. 11.7. Взвешенный граф
N-периферия вершины v - это множество вершин, расстояние до каждой из которых (от вершины v) не меньше, чем N.
| Таможни | Государства | Площадь территории | Наличие наземной границы | Стоимость получения визы |
| Переезды | Города | Стоимость ночевки в гостинице | Дороги | Длина дороги |
| Супер-чайнворд | Слова | - | Совпадение конца и начала слов(возможность "сцепить" слова) | Длина пересекающихся частей |
| Карта | Государства | Цвет на карте | Наличие общей границы | - |
| Сеть | Компьютеры | - | Сетевой кабель | Стоимость кабеля |
